What Is An Unbalanced Force: Definition And Examples

In the context of physics, an unbalanced force is a force that causes a change in an object’s state of motion. Unbalanced forces are the things that make objects speed up or slow down.

Recall Newton’s first law of motion, which states:

NL1: “An object in a constant state of motion remains in that constant state of motion unless acted upon by an unbalanced force.”

Unbalanced forces are the things that make object deviate from their current state of motion. Forces are measured in Newtons (N), named after Isaac Newton.

Here is a simple example: Imagine a book lying at rest on top of a table. In this configuration, the force of gravity pushes down on the book. At the same time, the table, according to Newton’s third law, exerts an upward force on the book of equal magnitude and opposite direction as gravity (sometimes called the normal force). Because these forces are exactly equal and in opposite directions, they perfectly cancel out and the book does not change its state of motion. In this configuration, the book is at equilibrium and the two equal and opposite forces are called balanced.

The forces acting on the book are equal and opposite, so the book does not move. Credit: Author

Now, imagine what happens if we suddenly remove the table. Once we remove the table, there is no longer any upward force acting on the book. So, the force of gravity takes over and causes the book to accelerate towards the ground. In this situation, the forces are considered unbalanced. The reason the book moves is that the net force acting on it is non-zero. The downward force acting on it is greater than the upward force, so the book accelerates downward.

Unbalanced Force = Net Force

Let’s examine that phrase “net force.” Strictly, speaking, Newton’s first law should not just say “force” but “net force.” The net force acting on an object is the sum total of all the individual forces acting on the object. In our previous example, the book lying on the table has two distinct forces acting upon it, the downward force of gravity and the normal force of the table. We know that forces cause changes in motion, so why doesn’t the book move if it has two forces acting on it? The reason why is that the force from gravity and the normal force are equal in magnitude and opposite in direction.

Remember, forces are vector quantities, meaning that they have both a magnitude (“size”) and a direction. It is not enough to just say “a 60 N force;” you must say something like “a 60 N force in the rightward direction. Vector quantities, like numbers, can be added and subtracted.

So what happens if you add two forces that are equal in magnitude, one in the purely right direction and the other in the purely left direction? It is easy to see that the two forces would entirely cancel each other out, and the result is if the body has no force acting on it at all (i.e. it does not change its state of motion). The pure rightward component of one force is exactly compensated for by the pure left component of the other force.

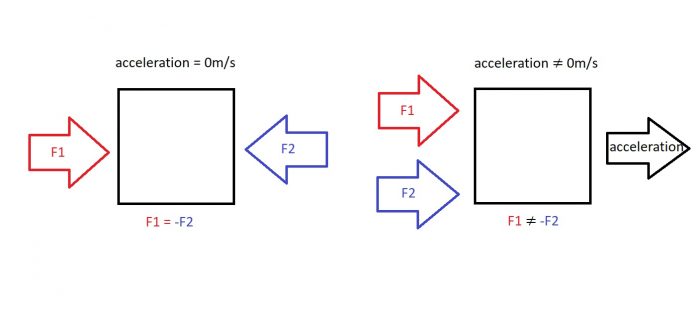
If two forces are balanced, they cancel out and the acceleration is 0. If they are unbalanced, the acceleration is not zero and the object changes its state of motion. Credit: Author

This is what is meant by the concept of “net force.” the net force acting on a body is the sum total of all the individual force vectors acting on the object. When this net force is non-zero, we say the forces are unbalanced. When the net force is 0, we say that the forces are balanced. If the net force is unbalanced, then the object will change its state of motion. The magnitude of acceleration is equal to the magnitude of the net force and the direction of acceleration is equal to the direction of the net force.

Examples Of Unbalanced Forces

Let’s return to our book example. In the configuration where the book is lying at rest on the table, the forces acting on the book are balanced (F_G = -F_N). Now, imagine that the book is sliding horizontally to the right across the table at a constant velocity (remember, there is no rightward force in this instance because forces are not required to maintain a constant state of motion, only change it). In this case, the force of gravity and the normal force are still balanced, but there is no rightward force to counteract the leftward force of friction. As the book moves to the right, the force of friction acts to the left. Since the force of friction is an unbalanced force, the book accelerates in the direction of the force of friction, i.e. the book slows down (remember, deceleration (slowing down) is just acceleration in a direction opposite the direction of velocity). The force is unbalanced, so it causes a change in the book’s motion.

Another example of an unbalanced force is the snapping action of a spring when let go after being pulled taut. Imagine a spring attached to a wall at one end. Next, pull the spring out and hold it there. In this configuration, the force of pulling is exactly equal and opposite to the force generated by the tension in the spring, so the spring is at equilibrium and does not move. When you let go of the spring, the forces become unbalanced and the spring rapidly snaps back together.

Another example of an unbalanced force is a rocket taking off. While on the ground, the downward and upward forces acting on the rocket cancel each other out and it stays at rest. When the rocket revs up its jets, the upward force suddenly exceeds the downward force from gravity, and the rocket accelerates upward.

The rocket rises upward because the force generated by its propulsion overcomes the force of gravity. Credit: Author

Another way of putting the point is that unbalanced forces exist in any case where some object changes how it is moving. Any time some object accelerates, we say that there is an unbalanced (net force ≠ 0) force acting on the object.

How To Tell If Forces Are Unbalanced

In order to find out if a particular object is being acted upon by a non-zero net force, you must first figure out the individual forces acting on the object and see if they combine to make a net force of 0. We will only consider the case of motion in one dimension to make the analysis easier.

Imagine a 5kg electric toy car is moving to the right and its engine applies 10 newtons of force. At the same time, a parachute attached to the back of the car exerts 7 newtons of force in the left direction. What is the net force acting o the car?

Since the forces are in the exact opposite directions, we can figure out the net force by just subtracting one force from the other.

10 N – 7 N = 3N

Therefore, the net force acting on the car is 3N in the rightward direction. How fast will the car accelerate? To figure that out, we can rely on Newton’s second law:

F=ma

So if a 3 N force was applied to a 5 kg car, then the car would accelerate:

3N = (5kg)a

3/5 = a

a = 0.6 m/s²

The toy car would accelerate 0.6 m/s²

So, this realization gives us a basic schema for figuring out if forces are unbalanced, and how that net force will cause a change in the object’s state of motion.

• Determine the individual forces acting on the object
• Combine all individual forces to get the net force
• Plug the net force and mass into F=ma
• Calculate acceleration

Here is another example to flesh out this process. A mass is situated on top of a spring. If the gravity pushes the mass down with 18N of force, and the spring pushes up with 40 N of force, what is the net force acting on the mass? Since the two forces are acting in the opposite direction, we can subtract one from the other:

40N – 18N = 22N

So the mass has a net force of 22 N acting on it in the upward direction.

So far, all of our examples have only considered motion in 1-dimension (left-right or up -down). Calculating the addition and subtraction of force vectors in 2- and 3-dimensions is much more difficult, but the same idea is true: you find the magnitude and direction of the net force by adding together the individual dimensional vector components. So in 2-D, if you object has an upward force and a rightward force acting on it, the direction of the net force will be some combination of those two vectors.

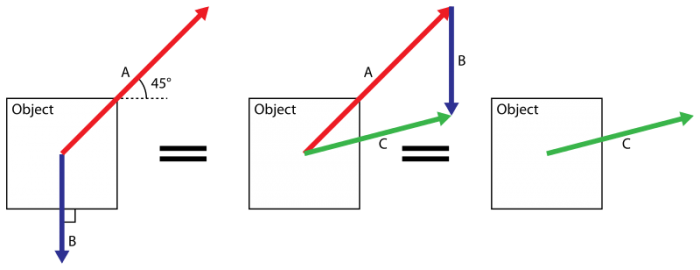
An example showing force addition in 2-dimensions. The net force is just the combined total of the individual forces. Credit: Raul645 via WikiCommons CC-BY SA 3.0

The simplest case of motion in 2-dimensions is projectile motion.