
One of the kinds of shapes studied in geometry and algebra is polygons. Polygons are shapes that are made out a finite number of straight lines that close off some area of space. Polygons are among the simplest kinds of shapes and have been rigorously investigated since the time of the ancient Greeks. The word “polygon” comes from two Greek words meaning “many angled.” All polygons have 3 essential properties:
- 1. They are 2-dimensional
- 2. They have an interior and exterior (they enclose some space)
- 3. They are made out of straight lines
Elements Of Polygons
All polygons can be broken down into parts. The individual line segments are called the edges or sides and the points where the edges meet are called vertices (sing. vertex). The area enclosed by a polygon is called the body. A diagonal of a polygon is any line segment that can be drawn to connect two nonadjacent vertices.

The parts of a polygon. Credit: Author
Classification Of Polygons
Polygons can be classified in a number of ways relating to:
- number of sides
- convex or concave
- self-intersecting or simple
- regular or irregular
Number of Sides
Most of the time, polygons are classified based on the number of their sides. According to Euclidean geometry, the smallest possible number of sides a polygon can have is 3. It takes at least 3 straight lines to enclose some area of space. Therefore, the triangle is the absolute simplest possible polygon in Euclidean geometry. Most polygons have a special name corresponding to the number of sides (quadrilateral-4 sides, pentagon-5 sides, hexagon, 6 sides, etc) or they can just be called an n-gon, where n corresponds to the number of sides (3-gon, 4-gon, 5-gon, etc).
What about a circle? Is a circle considered a polygon? The answer is no, a circle is not considered a polygon. This is because a circle is not made out of straight lines, it is a curve.
Convex or concave
Polygons can be classified as convex or concave. A convex polygon is any polygon whose interior angles are all less than 180 degrees. This means that every diagonal of a convex polygon will fall inside the area enclosed by the shape. In contrast, a concave polygon is any polygon that has at least one angle whose measure is greater than 180 degrees. A concave polygon will always have at least one diagonal that falls outside of the area enclosed by the shape.
Self-intersecting or simple
Polygons are also differentiated as self-intersecting or simple. A self-intersecting polygon has at least one pair of lines that intersect. In contrast, a simple polygon has lines that do not intersect each other. Self-intersecting polygons are sometimes called complex polygons. They can be somewhat tough to imagine. Imagine an elastic simple polygon that is picked up and twisted so that some of its sides cross each other. For example, a rectangle would turn in to a bowtie-like shape. In a self-intersecting polygon, the intersection of the lines does NOT create a new vertex or a new interior angle. The bowtie shape made form the square still has 4 interior angles and 4 vertices.
Regular or Irregular
Polygons are also classified according to their symmetries. A regular polygon is one in which all sides are equal length and all angles are of equal magnitude. An irregular polygon is one in which the sides and angles are unequal measures. For example, a square is a regular quadrilateral. The angles and sides of a square are all equal.
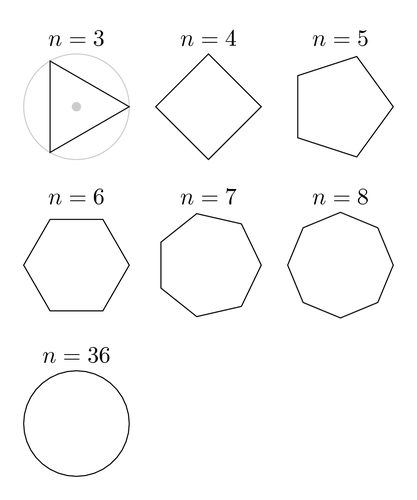
The first few regular polygons. Credit: Texample CC-BY SA 2.5
Angles Of Polygons
Every polygon has an equal number of sides and vertices. Thus, every polygon has an equal number of vertices and angle. For any simple polygon, the sum of its interior angles can be determined by the formula:
Angle = (n−2)×180
So, a square has interior angles that sum to 360 degrees ((4−2)×180), the interior angles of a hexagon sum to 720 degrees ((6−2)×180). This formula falls out of the fact that any simple polygon can be divided into n−2 triangles, each of which has interior angles that sum to 180 degrees (or pi radians). For any regular polygon, the measure and each interior angle is just the sum of the interior angles divided by the number of sides. So each angle of a regular triangle is 60 degrees (180/3), each angle of a regular pentagon is 108 degrees (540/5) and each angle of a 7-gon (heptagon) is 128.57 degrees.
Area Of Polygons
In this section, we will cover how to find the interior angle of polygons. Our analysis will focus on discovering the area of regular polygons as those have determinate formulas that are the same regardless of the size of the polygon. Irregular polygons do have general formulas, but that is a much more difficult mathematical problem to work out.
For any regular polygon with n sides of length s, the general formula for the area is:
Area = (n × s × a)/2
where a is the apothem; the length of a line drawn from the center perpendicular to one of the sides. In this expression, the quantity n × s is equal to the perimeter (length of sides × number of sides) so the expression can be written as:
Area = P × a/2
Figuring out the apothem is a bit trickier. The apothem is the shortest distance from the center to one of the sides creating a right angle. The formula for finding the apothem of an n-gon is:
a = s/2tan(180/n)
In English: the apothem is equal to the length of side s divided by two times the tangent of 180 divided by the number of sides n.
Let’s try this formula with a simple example: Say we have a hexagon with sides of length 10. A hexagon has 6 sides so we can calculate the perimeter as:
P = 6 × 10 = 60
To find the apothem, we plug in the values of n and s into the apothem formula:
a = 10/2tan(180/6)
a = 8.66
Plugging P and a into the full formula gives us:
Area = (60×8.66)/2
Area = 259.8 sq. units
So a regular hexagon with sides of length 10 has an area of 259.8 sq. units.
How To Understand The Area Formula
Why does this formula work? First, consider the fact that the interior of any regular polygon can be divided up into equal triangles.
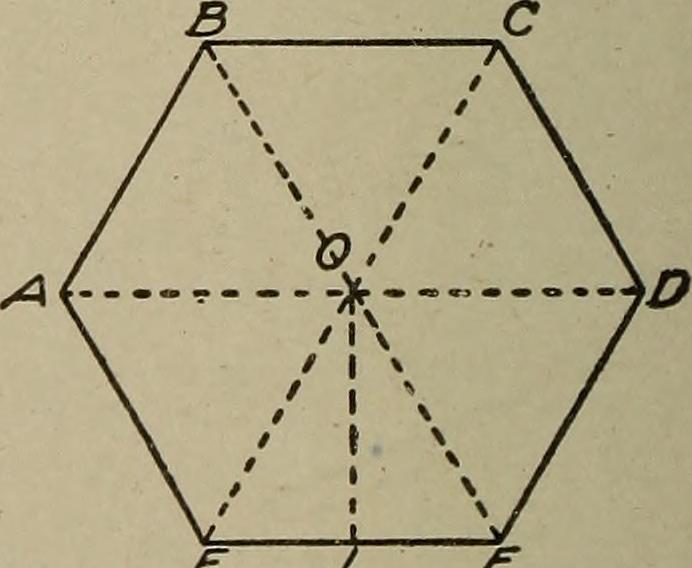
Credit: Public Domain
Each side can be seen as the base of each triangle, and the apothem is the height of each triangle. So, the area formula can be seen as simply the formula for the area of a triangle multiplied by the number of triangles.
Examples Of Regular Polygons
Below is a list of different regular polygons and some of their unique properties.
| Name | Edges | Properties |
| triangle | 3 | The simplest possible polygon in Euclidean geometry. Can make tessellations |
| quadrilateral | 4 | The simplest polygon that can be concave or self-intersecting. Can make tessellations |
| pentagon | 5 | The simplest polygon that can be a star |
| hexagon | 6 | The last of the regular polygons that can tessellate the plane |
| heptagon | 7 | The first polygon that cannot be constructed with a compass and straight edge |
| octagon | 8 | Each internal angle of an octagon is 135 degrees |
| nonagon | 9 | Cannot be constructed with a compass and straight edge |
| decagon | 10 | Uses the golden ratio to construct with a compass and straight edge |
| hendecagon | 11 | Cannot be constructed with compass and straight edge |
| heptadecagon | 17 | Discovered to be constructible in 1796 by Gauss. The first new regular polygon discovered in over 2000 years |
| hectogon | 100 | |
| chiliagon | 1000 | Used in philosophical thought experiments by Descartes. Ex. of a well-defined polygon that cannot be visualized |
| 65537-gon | 65537 | First constructed in 1894 by Johanne Hermes |
| apeirogon | countably infinite | A degenerate polygon that is equivalent (but not identical) to a circle. |
Polygons In Higher Dimensions
The word “polygon” usually refers specifically to 2-dimensional shapes that are made out of straight lines. The concept of a polygon can be generalized to higher dimensions. The generalization of a polygon is called a polytope. So a polygon is a specific 2-dimensional instance of the more general idea of a polytope.
Polytopes of a particular dimension n can be understood as being constructed out of elements of dimension n−1. For instance, a 2-D polytope (polygon) is made out of 1-D elements, i.e. lines. Similarly, a 3-D polytope is called a polyhedron (pl. polyhedra) and is a 3-D solid made out of 2-D polygons.
Unlike regular polygons, of which there exist virtually an infinite amount, there only exist 5 regular polyhedra in 3-D space. Theses 5 regular polyhedra are the tetrahedron, cube, octahedron, dodecahedron, and the icosahedron. These 5 regular polyhedra are sometimes called the “Platonic solids,” named after the Greek philosopher Plato who believed that the regular polyhedra were the shapes of the 5 classical elements fire (tetrahedron), earth (cube), water (icosahedron), and air (octahedron). The last regular polyhedra, the dodecahedron, was associated with the aether, the 5th classical element that was said to compose the heavens and celestial objects like the sun, moon, planets, and stars.
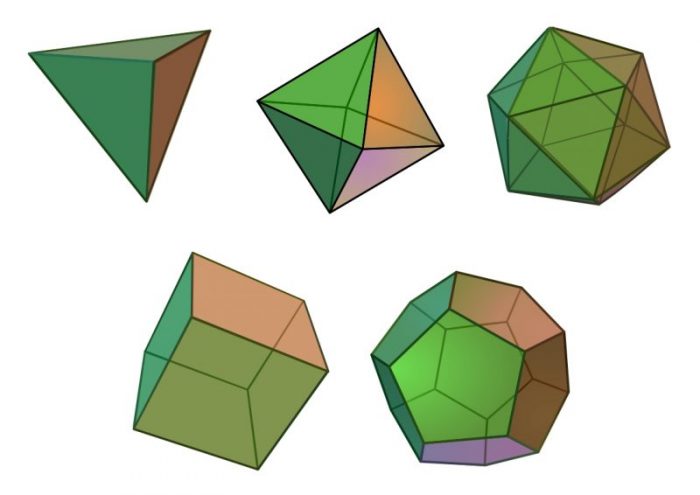
The 5 “Platonic solids” Credit: WikiCommons CC-BY SA 4.0
Why are there only 5 regular polyhedra? The answer has to do with the interior angles of 3-dimensional shapes. In short, 2-D polygons can be arranged into a regular 3-D polyhedron if the interior angles of at least three polygons that meet at a particular vertex sum to less than 360 degrees.
So think of a triangle. The interior angles of a regular triangle are all 60 degrees. The means we can have a polyhedron that has vertices where 3, 4, and 5 triangles meet:
3×60 < 360
4×60 < 360
5×60 < 360
These correspond to the tetrahedron, octahedron, and icosahedron.
In the case of a square, only 3 squares can meet at a vertex and have their interior angle sum to less than 360 degrees. The angles of a square are each 90 degrees, so:
3×90 <360
This corresponds to the cube. For pentagons, it is only possible to have 3 pentagons meet at a vertex and have the interior angles sum to less than 360:
3×108 <360
This arrangement corresponds to the dodecahedron.
What about hexagons? The answer is NO. You cannot make a regular polyhedron out of regular hexagons. This is becaue the interior angles of at least 3 hexagons that meet at a single vertex add up to 360 degrees. Therefore, that arrangement of hexagons can only exist in 2-D space; there is no “extra” space left for the shape to bend into 3 dimensions.
So the hexagon is the first of the regular polygons that cannot be used to make a regular polyhedron. In fact, no other shapes except for the triangle, square, and pentagon can make a regular polyhedron; the laws of 3-D space make it impossible.








