What Is Pi (Definitely Not Pie)?

If you remember anything from high school math, odds are you remember pi (and no, we don’t mean the delicious pastry). In mathematics, pi (represented with the Greek letter π) is an important number and mathematical constant.  Pi is most often seen in the context of circles and is exactly defined as the ratio of the circumference of a circle to its diameter:

π = C/d

Pi also pops up in the formula for the square area of a circle, which is:

A = πr²

where r is the radius of the circle. Aside from these two well-known formulas, the number pi rears its head all over the place in mathematics and science, often in unexpected circumstances. The number pi has been known to humans since at least the Babylonians in 4,000 BCE and, along with the numbers 0, 1, φ (golden ratio) and e, is often considered one of the most important numbers.

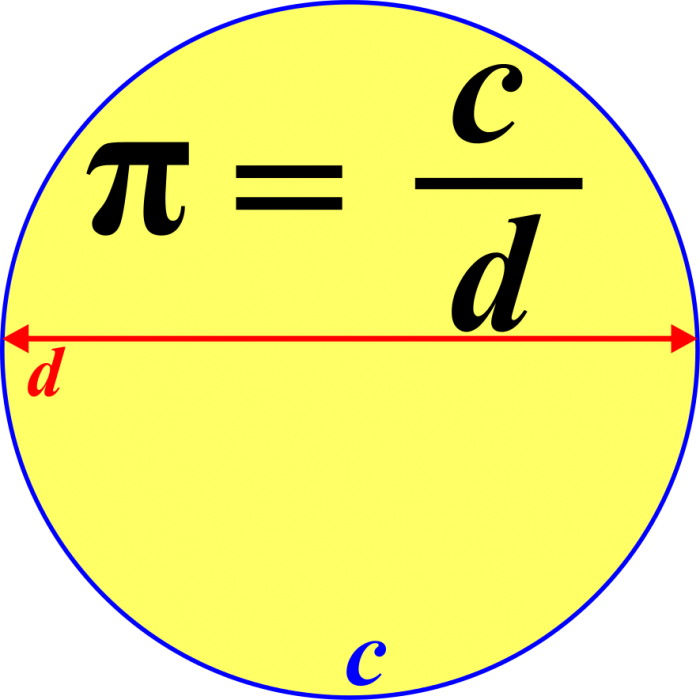
Pi is defined as the ratio between the circumference of a circle and its diameter. Credit: lantresmand via Wikipedia CC-BY SA 3.0

Properties of Pi

Pi has some strange properties that make it interesting to mathematicians. First off, pi is a constant, meaning that it stays the same. No matter how big your circle is, the ratio of the circumference to the diameter always works out to pi. Even if your circle has a massive diameter, the ratio of the circumference of the circle to that diameter will always equal pi.

Second, pi is what mathematicians call an irrational number. An irrational number is a number that cannot be expressed as the ratio of two integers. This means that pi cannot be expressed as some finite sequence of digits or as an infinitely repeating sequence of digits. In its decimal expansion, pi is given an approximate value of 3.14159. In actuality, the “real” decimal expansion of pi has infinite digits which never repeat; it just goes on and on forever never falling into some predictable pattern. Even though it is irrational, scientists and engineers often use rational numbers to approximate its value (22/7 or 333/106). Currently, pi has been calculated out to over 31.4 trillion digits (incidentally, the last digit in this computation is 0).

The first 175 digits of pi. Credit: Pixabay CC0 1.0

Third, pi is also what is known as a transcendental number. This means that pi cannot be a solution to any polynomial equation with rational coefficients; equations like 4x³+x²−6x = 0 or (x⁵/120)−(x³/60)+x = 0. Functionally, the transcendental nature of pi means that you cannot construct pi by some finite series of rational numbers and roots. In other words, you cannot “build” the number pi by performing algebraic manipulations on rational numbers and their roots, like you can with, say, 37 or √2. Pi being transcendental also explains another old question in mathematics: whether it is possible using only a compass and straightedge to construct a square with the same area as a given circle. It was proven in 1882 that this is impossible: you cannot construct a square of equal area from a given circle using only a compass and a straightedge. It is impossible precisely because pi is a transcendental number and cannot be constructed by some finite set of arithmetic steps which is all a compass and straightedge can do.

Where Does Pi Come From?

Let’s take a step back from these technical definitions and think about circles and geometry. If you have a piece of string, perform the following experiment: fasten a thumbtack to one end of the string and stick it onto a piece of paper. Tie the other end to a pencil and, while stretching the string taut, trace out an arc around the center point with the pencil. If done correctly, you will have drawn a circle with a radius that is the length of the piece of string you used.

Next, take that piece of string and lay it along the circumference of the circle you drew. See how many string lengths will fit onto the circumference. You should find that no matter how long your string is or how big your circle is, the string will fit into the circumference the same amount of times, just a little over 6 times in fact. Since the radius is half the length of the diameter, the diameter would fit onto the circumference half as many times. The amount of times the diameter fits on the circumference is equal to pi (≈ 3.14159).

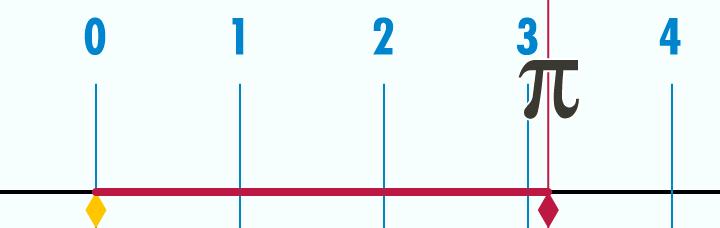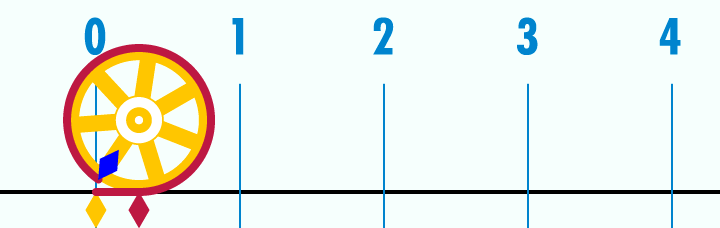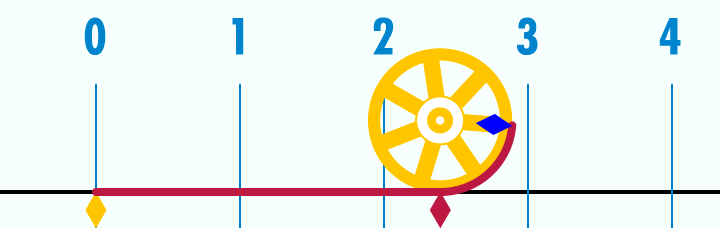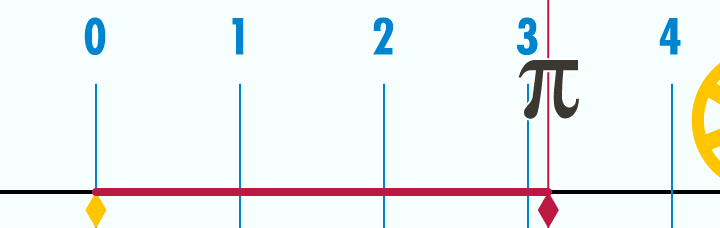
Here is another way to visualize the relationship between circles and pi. Imagine you have a circle that has a diameter of 1 unit (the choice of units is not important because the value of pi will always be the same). Pick a point on the circumference of a circle and place it on a number line at 0. Next, from that point, imagine “unrolling” the entire outside of the circle into a flat line. When the circle is completely unrolled, the line will be exactly π units long.

Credit: John Reid via WikiCommons CC-BY SA 3.0

Formulas That Use Pi

Most of the time, pi is introduced to students in the context of geometry. In geometry, pi is an important value that is related to circles, curves, ellipsoids, and spheres. Some of the more common formulas in geometry that use pi are:

• Circumference = d × π
• Area of a circle = πr²
• Area of a sphere = (4/3)πr³
• Surface area of a sphere = 4πr²

The first formula is easy and follows as a direct consequence of the definition of pi as the ratio of the circumference of the circle to its diameter.

The area formula is a bit trickier. At first glance, it may not seem obvious that the area of a circle is equal to the radius squared multiplied by π. However, we can use a clever bit of geometry to see why this must be the case.

Imagine we start with some regular polygon that is inscribed inside of a circle, let’s say an octagon.

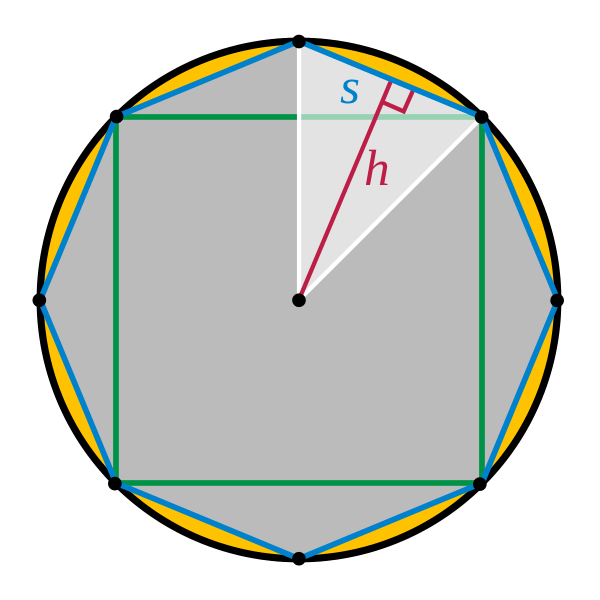
Credit: Ksmrq via WikiCommons CC-BY SA 3.0

First, notice that if we were to continually increase the number of sides of the polygon, it starts to resemble more and more a circle. A polygon with an “infinite” amount of sides would be identical to a circle. Second, notice that any polygon of n sides can be divided into n triangles of equal area. The dimensions of each of these triangles are:

s – the side length of the polygon

h – the height of each triangle

r – the radius of the polygon and the circle

the area of a triangle is ½ b × h so the area of each triangle inside the polygon is:

½hs

For a polygon with n triangles (and so n sides) the entire interior area of the polygon is:

polygon area = n × ½hs

This can be rearranged into:

polygon area = h/2(ns)

The term ns represents the perimeter of the polygon (n sides of length s). As the number of sides goes to infinity, the perimeter gets closer and closer to a circle which is just 2πr. We can place this in the equation to get:

polygon area = h/2(2πr)

As the number of triangles goes to infinity, each triangle gets narrower. As s goes to zero, h and r become the same length. So substituting r for h we get:

polygon area = r/2(2πr)

which of course simplifies into:

area = πr²

So by approximating the area of a circle with a polygon of an increasing number of sides, we get the formula for the area of a circle. Q.E.D. This particular proof is due to the Greek mathematician Archimedes who lived in the 3rd century BCE.

The proofs for the area and surface area of a sphere are more complicated but rest on similar reasoning. Essentially, the formulas pop out via the process of successive approximation of the dimensions of a curve by smaller and smaller polygons.

Pi also pops up in trigonometry in the context of the sine and cosine functions. The periodic nature of waves gives them a certain “circular” quality which can be defined in terms of the unit circle and right triangles. Because the definitions of the trig functions are derived from a unit circle, it is no surprise that π pops up in equations related to those functions. As a consequence, π often pops up in physics in the context of modeling periodic motion, like the bouncing of a spring or the oscillation of a transverse wave.

History Of Pi

Pi has been known by humans probably since pre-history. The first written records of the number pi come from the ancient Babylonians. According to texts dated to the 17th century BCE, the Babylonians used the numerical value 25/8 as an approximation for π. Documents from ancient Egypt show that the Egyptians used the value (16/9)². Both of these approximations are extremely close to the actual value of pi. In general, these early computations of π were likely derived simply from drawing circles and measuring their circumferences.

It was not until the Greeks that mathematicians came up with the first algorithm that could be used to compute pi. Archimedes in 250 BCE devised a geometric method to approximate pi to arbitrary precision. His method was based on inscribing polygons in circles and doubling their sides. Using his method, Archimedes deduced that the value of π must be somewhere between 223/71 and 22/7. For over 1,000 years the Archimedean method for computing pi was the standard.

It was not until the 16th and 17th century with the development of infinite series techniques that mathematicians found a better way to compute the value of pi. The first recognized infinite series proof for calculating pi is found in the work of the Indian mathematician Madhava of Sangamagrama. Several other mathematicians such as Gottfried Leibniz and Leonhard Euler devised ingenious ways of computing the digits of pi from infinite series.

With the rise of computing technologies in the 20th century, the hunt for the digits of pi entered a new phase. Now, mathematicians could mechanically compute the digits of pi to millions and even billions of digits. The largest every computation of the digits of pi was achieved in 2019 by Japanese computer scientist Emma Haruka Iwao who calculated pi out to 31,415,926,535,897 digits.