Transverse Waves Examples

How does a guitar make noise? Anyone who has seen guitars knows that they make noise by the vibration of the strings. Plucking a string causes it to vibrate at a certain rate which produces the pleasant twang associated with both the jazzy tones of Mark Knopfler and the bleeding solos of Slash from Guns N’ Roses

The motion of the string produces a wave-like pattern. Specifically, it creates a transverse wave. A transverse wave is a wave that oscillates perpendicular to the direction of its propagation. Examples of transverse waves include a plucked guitar string, waves in water, the motion created by waving a string, and light. A transverse wave is contrasted with a longitudinal wave—a wave that oscillates in the same direction as its propagation. Longitudinal waves are sometimes called “compression waves” or “pressure waves” because they cause compression and changes in pressure in their mediums. Some wave, like seismic waves during an earthquake, have components of both transverse and longitudinal waves.

Vibrations and waves are extremely important in physics as many physical phenomena take the form of some kind of periodic wave-like motion. A guitar string’s motion can be described as a transverse wave because it oscillates up and down perpendicular to its axis of motion (incidentally, the actual sound wave produced by the string and perceived by the ear is a longitudinal wave, but focus on the motion of the string itself for now).

Components Of A Transverse Wave

Here is a simple diagram of a transverse wave that identifies its components:

The components of a transverse wave. Credit: G Ruth via WikiCommons CC BY-SA 3.0

A transverse wave has the following parts:

crest: the high point (top) of the wave

trough: the lowest point (bottom) of the wave

amplitude: height of the wave relative the axis of motion

wavelength: length between each crest or each trough

Transverse waves also have a frequency, the rate at which each crest of the wave passes through a given point per unit of time. Frequency can be seen as how quickly the wave is oscillating up and down. The higher the frequency, the more oscillations pass through a given point for each unit of time. Frequency is measured in hertz (Hz). One hertz equals one oscillation per second.

Back to the guitar string. The vibration of the guitar string is a transverse wave. The frequency of the wave is how quickly the string is vibrating and corresponds to the pitch of the note you hear. For example, a standard A note on the guitar has a frequency of 110 Hz, meaning that it oscillates 110 cycles per second. The higher the frequency, the more vibrations per second and the higher the sound. The high B string on a guitar has a frequency of about 246.96 Hz.

Guitars can be loud or soft too. The loudness of the string corresponds to the amplitude of its vibration; the height of each wave. Plucking a string very hard produces big waves and makes a loud sound while plucking softly produces small waves and a quieter sound.

Lastly, there is the notion of phase.  Say we pluck the A string on one guitar, let it ring for a bit, then pluck the A string on another guitar. Even though the two strings have the same frequency and amplitude, we can still tell there are two notes because the waves do not perfectly sync up and blend in with each other. The phase of a wave is a measure of how off-set the horizontal motion of the wave is from some perpendicular origin. The phase tells you the relative displacement between corresponding features of waves with the same frequency.

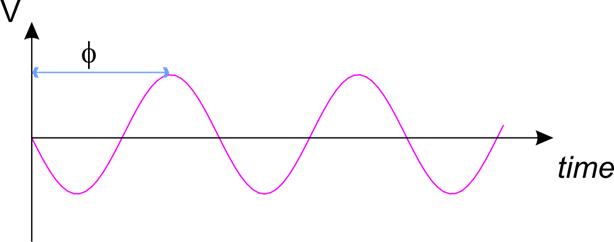
The phase is a measure of horizontal offset of a wave. Credit: Farzad via Wikipedia CC BY-3.0

Waves travel at a particular speed. The speed of propagation of a wave is equal to the product of its wavelength and frequency:

v = fλ

where f stands for frequency and λ (“lambda”) stands for wavelength. For example, if a given wave oscillates at a rate of 3 hertz and has a wavelength of 35cm, then that wave has a speed of propagation v = (3)(35)=105 cm/s. This mathematical relationship allows us to predict how features of a given wave will change if other features are held constant. If the frequency of the wave changes but its velocity remains constant, then its wavelength must change to compensate. Likewise, if the wavelength changes but the speed stay constant, the frequency of the wave must change.

Concept Check

Q1.) A wave on a string has a frequency of 7 Hz and a wavelength of 3cm. If the frequency changes to 15 Hz and the velocity of the wave remains the same, what is the new wavelength?

Q2.) Say a wave has a velocity of 60 m/s and a frequency of 323 Hz. If the velocity changes to 24 m/s but the frequency remains the same, what is the difference between the initial wavelength and the final wavelength?

Q3.) A wave with a frequency of 116 Hz and a wavelength of 5,800 nm is changed so that its frequency is 323 Hz and wavelength is 1,285 nm. What is the difference between the initial speed of the wave and the final speed?

Answers

Q1.) If the wave initially has a frequency of 7 Hz and a wavelength of 3 cm, its initial velocity is 7 × 3cm = 21 cm/s. Since velocity remains constant, we know that the equation for the wave after changing it is:

21 cm/s = 15 Hz × λ

Solving for λ gives us:

21 cm/s = 15 Hz × λ

21/15 = λ

λ = 1.4 cm

The wavelength of the modified wave is 1.4 cm.

Q2.) First, we need to figure out the initial wavelength of the wave. If the initial velocity is 60 m/s and the initial frequency is 323 Hz, we know that the initial wavelength is:

v = fλ

60m/s = 323(λ)

60/323 = λ

λ = 0.19 m.

The initial wavelength is 0.19 meters. Now we need to find the final wavelength. if the final velocity is 24 m/s and the frequency stays the same (323 Hz), then the final wavelength is:

24/323 = λ

λ = 0.07 m

Subtracting the two values gives us 0.19 m − 0.07 m = 0.12 m. The final wave has a 0.12 meter shorter wavelength.

Q3.) The initial velocity of the wave is given by:

v = 116 Hz × 5,800 nm

v = 627,800 nm/s

If the frequency changes to 323 Hz and the wavelength to 1285 nm, the final velocity is:

v = 323 Hz × 1285

v = 415005 nm/s

Finding the difference of these two give us: 627,800 nm/s−415,005 m/s = 212,795 nm/s. The final wave is going 212,796 nm/s slower than the initial wave.

General Equation For Wave Motion

Waves are a periodic kind of motion, meaning that their motion repeats over a given amount of time (frequency). In mathematics, two equations that are particularly useful for modeling waves are the sine and cosine functions:

ƒ(t) = sin(t)

ƒ(t) = cos(t)

Graphing these two functions produces a nice periodic wave shape. For more information on why sine and cosine are periodic functions that repeat, read this article on basic trig functions.

The general function describing the motion of a transverse wave with respect to time t is:

ƒ(t) = Asin(2πft + φ)

Where A is equal to the amplitude, f is the frequency, and φ is the phase. manipulating the parameters has the following effect on the wave: Increasing A makes the individual waves taller while decreasing it makes them smaller. Increasing f makes the crests of the waves narrower and closer together, and changing φ changes the phase of the wave; i.e. how great its horizontal offset is.

Waves And Energy

When we say a wave “moves,” what exactly is moving? Waves transfer energy, not mass. Imagine a ball bobbing in the tide. As the wave “moves” (propagates) towards the shore, the ball itself will not move towards the shore. Instead, it will move up and down perpendicular to the wave’s propagation. Eventually, the ball will move to the shore because of the wind or the tide, but not because of the wave itself.

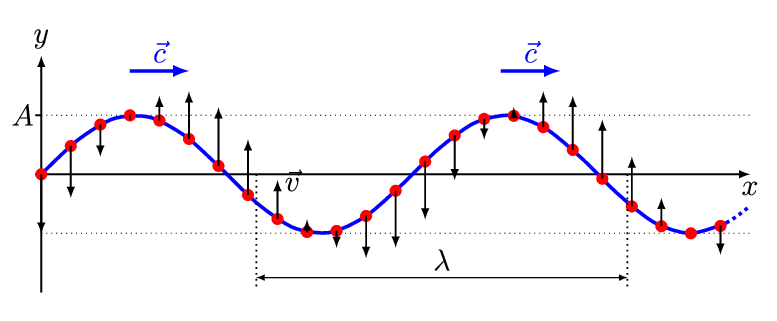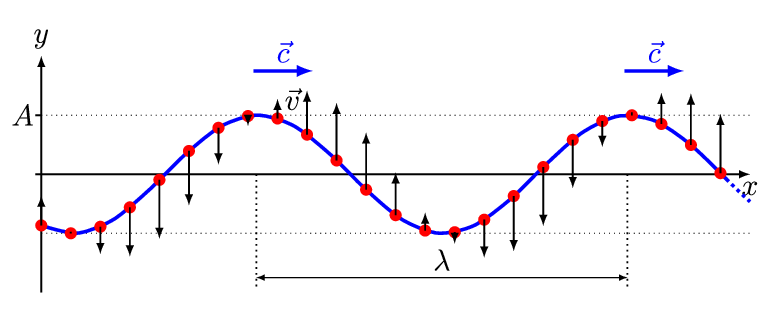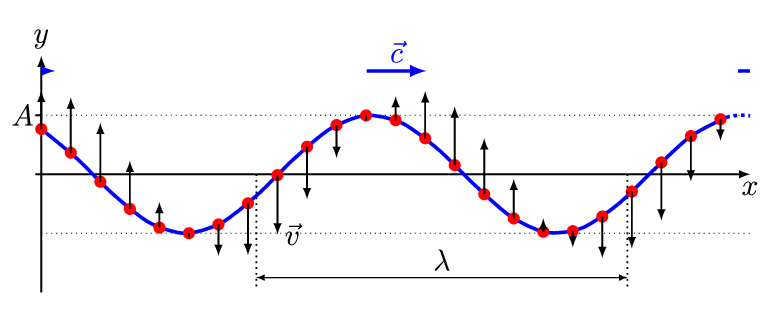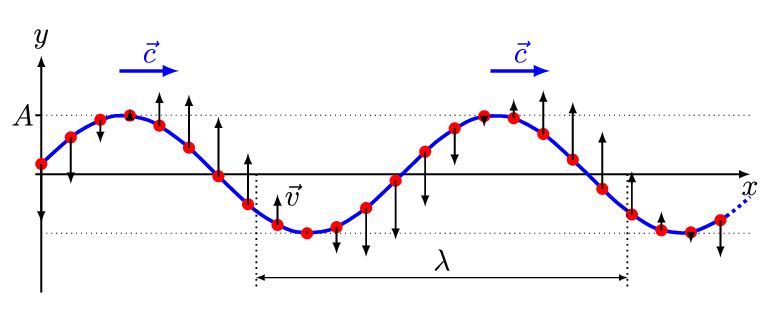
Credit: And1mu via WikiCommons CC BY-SA 4.0

In the above image, notice how each red point only moves perpendicular to the direction of propagation. Transverse waves do not move particles in the direction of propagation but they carry an impulse of energy through a medium. When we refer to the “motion” or “speed” of a wave, we are referring to the speed at which the energy propagates through the wave, not the rate at which the individual points in the wave are moving. The amount of energy carried by a wave is directly proportional to the square of its amplitude.

The fact that waves carry energy explains another unique feature of waves. What happens if two particles try to exist in the same location at once? They would collide into each other and one would crowd the other out of the space. What about if two waves exist in the same location at once? Waves are different than particles. Instead of crowding each other out, if two waves meet they interfere to form a new wave. Wave interference can be either constructive or destructive, depending on how exactly the waves interact.  When two waves meet, the combine their energy to make a new wave with a different amount of energy.