How To Convert Torr To Atm / Atm to Torr

Both the torr and atmosphere (atm) are units of pressure. One torr is exactly equal to 1/760 atm of pressure. Converting from torr to atmosphere is as simple as dividing the pressure value by 760. Likewise, in order to convert from atm to torr, just multiply by 760. In general:

atm = torr/760

torr = atm×760 

For example, 1432 torr is equivalent to 1.88 atm, and 4.6 atm is equal to 3,496 torr.

Neither the torr nor the atm is an SI unit of pressure. The SI unit of pressure is the pascal and is defined as a pressure equal to 1 newton of force per 1 square meter. Both torrs and atms can be converted into pascals. Torr can be converted into pascals by multiplying by 133.322 and pascals into torr by dividing by 133.322. To convert from atm to pascals, just multiply by 101325, and divide by 101325 to convert from pascals to atm:

pascal = torr × 133.322

pascal = atm ×101325

Sample Questions:

1. Convert 3.48 atm to torr
2. Convert 3265.7 Torr to atm
3. Convert 120 Torr to pascal
4. Convert 6.8 atm to pascal
5. Convert 15 pascals to atm

Answers:

1. 3.48 atm × 760 = 2644.8 Torr
2. 3265.7 Torr ÷ 760 = 4.3 atm
3. 120 Torr × 133.322  = 15998.64 pascal
4. 6.8 atm × 101325 = 689010
5. 15 pascal ÷ 101325 = 0.000148 atm

What Is Pressure?

Pressure in the context of physics and chemistry is the force exerted on a surface per unit area of that surface. In its most basic terms, pressure is mathematically defined as the magnitude of a force exerted perpendicular to a surface divided by the total surface area:

P = F/A

Unlike vectors like force, acceleration, or velocity that have both a magnitude and direction, pressure is a scalar quantity and only has a magnitude. At its base, pressure is the force that one substance exerts on another substance per unit of area.

As an example, say we have a static cloud of gas. Although it does not appear to be moving, the gas is made up of billions and billions of tiny particles in random motion. If we put the gas in a container, we would detect an ambient pressure from the gas, caused by molecular collisions with the walls of the container. Shrinking the container smaller would increase the pressure, as the gas would have less space to move and it would hit the container walls more. The molecules exert more force per unit area so the pressure increases.

With this simple example, we can immediately determine a few things about how pressure works. First, we can see that the magnitude of pressure is inversely proportional to the area over which the force is distributed. Take a thumbtack for example. Pushing on a wall with your finger will not dent or leave a mark in the wall. However, pushing with the same force while using a thumbtack can punch through the wall as the force is concentrated into the point of the thumbtack. Concentrating the same force over a smaller area results in an increase in pressure. The same principle is behind the operation of a knife. If you tried to cut with the flat edge of a knife it will not be very effective. Turning the knife on its sharp edge makes it more effective at cutting as the applied force is concentrated over a smaller area. Likewise, a large force can exert a small pressure if that force is distributed over a large surface area.

There are several different kinds of pressure but all of them are expressed in terms of a perpendicular force exerted over some area.

Atmospheric Pressure

Most uses of the concept of pressure are related to atmospheric pressure—the pressure exerted on the surface of the Earth by the weight of Earth’s atmosphere. The atmospheric pressure is a result of the gravitational attraction of Earth on gases above its surface. The atmospheric or Earth and other planets is determined by the planet’s mass, radius, and composition of the atmosphere.

Atmospheric pressure can be measured by a device called a barometer. The first barometers consisted of a vertical glass tube filled with some liquid (usually water or mercury) inverted over a liquid container open to the atmosphere. Earth’s atmosphere pushes on the surface of the liquid in the open reservoir, forcing liquid up the tube a certain height. The exact height of the liquid in the tube depends on the density of the liquid. Changes in atmospheric pressure result in a change in the height of the liquid in the tube.

An old mercury barometer. Credit P VanDerWerf via Flickr CC BY 2.0

Historically, standard atmospheric pressure is defined as the amount of pressure required to lift a column of mercury in a barometer 760 mm high. This amount is defined as 1 atm of pressure and is equal to 101325 pascals. This is equivalent to about 14 pounds per square inch, meaning that, at any given moment, Earth’s atmosphere is pushing on each square inch your body with 14 pounds of pressure. The reason we do not notice this pressure is because the pressure is exerted equally in all directions, which keeps your body from collapsing under the weight.

Standard atmospheric pressure is important in chemistry where it is used as a reference point for chemical experiments. The physical properties of a substance depend on surrounding temperatures and pressures so it is required to note pressures when describing the behavior of a substance. For example, the boiling and melting points of most common chemical compounds are recorded at 1 atm of pressure. In other words, water has a boiling point of 100 °C only at 1 atm of pressure. Higher pressures raise the boiling point and reducing pressure lowers boiling point.

Ideal Gas And Pressure

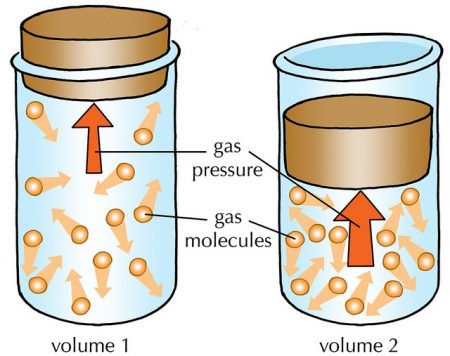
One of the most common places chemistry students encounters the concept of pressure is in state equations that describe the behavior of gases. Two of the simplest laws describing the pressure of a gas are Boyle’s law and Gay-Lussac’s law. Boyle law states that for a constant amount of gas at a constant temperature, the pressure exerted by the gas is inversely proportional to the volume of the gas: Mathematically this is:

P ∝ 1/V, or

PV = k

where k is a constant. This law is intuitive: if the amount of gas stays the same, then reducing the volume of the gases container means that more molecules hit the walls and cause greater pressure. If the container is larger, the force of the molecules is distributed over a larger area so there is less pressure.

Charles’ Law. As volume decreases, pressure increases. Credit: Siyavula Education via Flickr CC BY 2.0

Gay Lussac’s law describes the relationship between pressure and temperature. Gay-Lussac’s law states that the pressure of a fixed quantity and volume of gas is directly proportional to its temperature. mathematically this law is:

P ∝ T, or

P/T = k

Temperature is simply the movement of molecules. Raising the temperature of a gas is the same as making the gas molecule move faster. The faster the molecules move, the more force they exert on the walls of their container. Thus, raising the temperature of gas should see an accompanying rise in pressure.

The various laws the describe the behaviors of gases can be combined into a single equation. The ideal gas equation PV = nRT has as one of its parameters pressure, denoted by P. Essentially, the ideal gas law tells us the relationship that holds between the physical properties of a gas: pressure (P), volume (V), amount of gas (n), and temperature (T). The R in the equation stands for the ideal gas constant, a constant of proportionality that relates the temperature and amount of a gas to its average kinetic energy.

These gas equations allow us to reason with and predict the behavior of a gas under various conditions. For example, say we have a sample of a fixed quantity of gas that has a volume of 2.30 L and a pressure of .86 atm. what would the pressure of the gas be if the volume were 3.60 L?

Boyle’s law tells us that for a fixed quantity of gas the product of the pressure and volume is a constant value. this means that the product of the pressure and volume in one state is equal to the product of pressure and volume in another state: P₁V₁ = P₂V₂. We can determine the volume of the gas at 1 atm by plugging in values and solving:

2.30(0.86) = (3.60)P

P = 0.55 atm

So the same sample of gas at a volume of 3.60L would have a pressure of 0.55 atm.

History Of Torr/Atm

The torr is named after the Italian physicist Evangelista Torricelli, the person who first invented and explained the mechanism behind the barometer. In the 17th century, Torricelli discovered that the raised liquid column of a barometer was caused by the force exerted by the Earth’s atmosphere on the liquid. He showed this to be the case by demonstrating that the height of the liquid in the column was directly dependent on the density of the liquid in the vial, a condition that would have held only if the cause of the liquid rising were pressure due to the atmosphere.

Torricelli noticed that at sea level, the Earth’s atmosphere was enough to raise a column of mercury 760 mm high. This value was defined as 1 atm of pressure, and the torr was defined as exactly 1/760th of this value, making 1 torr equal to 1 mm Hg. These values still serve as the reference point for pressure calculations, though now they are defined in terms of fundamental and derived SI units.