The Acceleration Formula (Equation) In Physics: How To Use It

The acceleration formula is one of the basic equations in physics, something you’ll want to make sure you study and practice. After all, acceleration is one of the building blocks of physics.

“A motion is said to be uniformly accelerated when, starting from rest, it acquires, during equal time-intervals, equal amounts of speed.” — Galileo Galilei, Two New Sciences, 1638

The general formula for average acceleration can be expressed as:

• acceleration = (v_Final−v_Initial)/(t_Final−t_Initial)

Where v stands for velocity and t stands for time. In algebraic notation, the formula can be expressed as:

• a=Δv/Δt

Acceleration can be defined as the rate of change of velocity with respect to time. Acceleration is one of the most basic concepts in modern physics, underpinning essentially every physical theory related to the motion of objects.

The SI unit for acceleration is meters per second per second (m/s²). Doubtless, everyone is familiar with the feeling of acceleration like when you press the gas pedal and are pushed back into your seat. In fact, almost every observable effect of motion comes from acceleration due to the influence of forces. Acceleration, like velocity, is a vector quantity, meaning that it has both a magnitude and a direction. Strictly speaking, there is no such thing as “deceleration,” just acceleration in the opposite direction.

Acceleration is one of the major parameters of motion. The parameters of displacement (d), velocity (v), and acceleration (a) all share a close mathematical relationship. Information about one of the parameters can be used to determine unknown information about the other parameters. In general, there are 4 major equations that relate these 3 parameters to each other and to time:

• d = v_it+(1/2)at²
• v_f = v_i+at
• v_f = v_i+2ad
• d = ((v_i+v_f)/2)t

These 4 equations can be used to predict unknown information about the motion of an object from known information about the motion of an object. So, if one knew an object’s acceleration, the distance it traveled, and its initial velocity, one can determine the object’s final velocity. Likewise, if one knew an object’s initial velocity, acceleration, and the elapsed time, they could determine how much distance it covered. Let’s consider some simple examples to illustrate the uses of these formulas.

“Acceleration is finite, I think according to some laws of physics.” — Terry Riley

Uses Of Acceleration Formulas

(1)

Say you are on a sailboat, specifically a 16-foot Hobie Cat. Initially, you are traveling at a velocity of 3 m/s. You catch a big gust of wind and, after 7 seconds, you are traveling at a velocity of 10 m/s. What was your average acceleration?

Plugging our values into our formula for average acceleration, we get a=(10−3)/7=7/7=1 m/s². The average acceleration of the boat was one meter per second per second. Another way of reading this value is by saying: for every second, your velocity increased by one meter per second.

(2)

An airplane beginning from rest begins to accelerate at a rate of 3 m/s² down the runway before finally lifting off the ground 32 seconds later. How far did the plane travel on the ground before lifting off?

In this question, we are given three pieces of information: the plane’s initial velocity (0m/s), the plane’s acceleration (3m/s²), and the duration of motion (32 seconds). Plugging these values into the first of the 4 equations given above:

• d = v_it+(1/2)at²

gives us:

• d = (0)(32)+(.5)(3)(32)²= 1536 meters.

That is, the plane traveled a total of 1536 meters before taking off.

“Gravity and acceleration are equivalent.” — Albert Einstein

(3)

A feather is dropped on the surface of the moon from a height of 8 meters. Acceleration due to gravity on the moon is 1.5m/s². How long does it take for the feather to hit the ground?

In this case, we are given the initial velocity (0m/s), the acceleration (1.5m/s²), and the total distance traveled (8m). Plugging these values into the first equation

• d = v_it+(1/2)at²

gives us:

• 8=(0)t+(0.5)(1.5)t²
• 8=(0.5)(1.5)t²
• 8=.75t²
• 10.66=t²
• 3.26 = t

So, the feather will take a total of 3.26 seconds to hit the surface of the moon.

(4)

Starting from rest, a rocket ship accelerates at 15m/s² for a distance of 650 m. What is the final velocity of the rocket ship?

In this case, we know the initial velocity (0m/s) the distance traveled (650m), and the rate of acceleration (15 m/s²). Plugging these values into the third equation:

• v_f = v_i+2ad

gives us:

• v_f = 0+2(15)(650)
• v_f = (30)(650)
• v_f = 19,500 m/s

The final velocity of the rocket ship is 19,500 m/s.

Instantaneous Acceleration

So far, we have only considered cases, where we have either the average acceleration or the acceleration is uniform. Just having the average acceleration of an object can leave out important information regarding that object’s motion though. Having just the average acceleration over a duration cannot tell you if an object’s acceleration changed over that duration. Maybe it started accelerating very slowly, then its acceleration increased over time. What we can do is split that duration up into smaller segments, and calculate the average acceleration for those segments, thus giving us more information about an object. So say we have some distance from A to E. We can split that distance up into 4 segments AB, BC, CD, and DE and calculate the average acceleration for each of those intervals.

Now, imagine we keep dividing that distance into smaller intervals and calculating the average acceleration over those intervals ad infinitum. Eventually, we would reach a point where we have an object’s acceleration at a single mathematical point. This is also known as its instantaneous acceleration — the acceleration an object has at a single point in time. An object’s instantaneous acceleration could be seen as the average acceleration of that object over an infinitesimally small interval of time. The concept of instantaneous acceleration is possibly the single most important concept in physics and forms the backbone for essentially all of Newtonian physics. One can determine an object’s instantaneous acceleration by using the tools of calculus to find the second derivative of an object’s displacement function or the first derivative of an object’s velocity function.

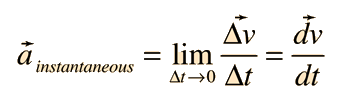
The formula for instantaneous acceleration in limit notation.

Summary

In summation, acceleration can be defined as the rate of change of velocity with respect to time and the formula expressing the average velocity of an object can be written as:

• a=Δv/Δt

The other 4 equations:

• d = v_it+(1/2)at²
• v_f = v_i+at
• v_f = v_i+2ad
• d = ((v_i+v_f)/2)t

also are important equation involve acceleration, and can be used to infer unknown facts about an object’s motion from known facts.