Velocity Equation (Formula): How To Find Velocity

The equation for velocity is one of the fundamental formulas in physics. While many physics concepts have scientific definitions different from their colloquial use, your intuitive perception of velocity is probably rather similar to its definition within physics. The velocity equation is:

v_avg = xf-x0/tf-t0

Velocity is just the rate of change in an object’s position with regards to a chosen point of reference, so the change in position divided by time. “Xf” is the final position of the object while “X0” is the initial position. Similarly, “Tf” is the final time frame while “T0” is the initial time frame.

“I like physics. I think it is the best science out of all three of them, because generally it’s more useful. You learn about speed and velocity and time, and that’s all clever stuff.” — Tom Felton

A large change in position in a small enough time means that the object has high velocity, while a small change in position over a larger amount of time means the object has a lower velocity.

The Equation For Velocity

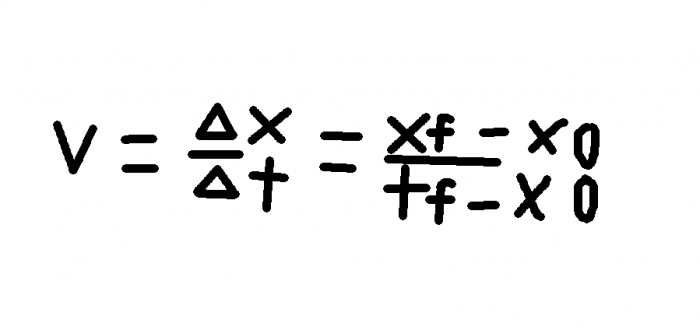
Photo: My Own

Velocity’s units of distance are divided by time. Think of how the velocity of the car is frequently given in kilometers-per-hour or mile-per-hour. The average velocity of an object can be defined as the change in an object’s position divided by the time spent traveling.

In the notation of the velocity formula, V(avg) is the object’s average velocity while Δx is the amount of change in the object’s position, referred to as displacement. X0 is the beginning position of the object at time t0, and Xf is the final position of the object at time tf. Note that when the starting time is given as zero, the equation for average velocity is given like this:

Vavg = Δx/t

In this equation, velocity is given as a vector. Vectors are geometric objects with both direction and magnitude, and as such, they can be used to track the movement of something through space. In reference to the velocity of an object, velocity is considered a vector because displacement is considered a vector (possessing both direction and magnitude). Velocity is usually given in meters per second, as meters is the International System of Units. However, you will frequently see velocity given in other units like miles-per-hour and kilometers-per-hour and even centimeters-a-second.

Examples

Let’s fill in the formula for velocity with a practical example:

If there is a someone walking down a sidewalk, beginning at the sidewalk’s far end, at the rate of -4 meters every five seconds (negative because they are moving left from their starting position), the rate of displacement could be expressed like this:

Vavg = Δx/t = -4m/5s = -0.8(m/s)

Notice that the velocity of a given object doesn’t provide us with information regarding how the person acted between their ending point and their starting point. Having only average velocity can’t tell us if the person tripped and therefore took longer to traverse the distance than they would have normally. You could break the distance of the trip into smaller sections and calculate those individual velocities to get more information about the trip. As an example, the total velocity of the trip, or Δxtot – could be represented as four different segments – Δxa, Δxb, Δxc , Δxd.

“Everything I do is somehow connected to velocity.” — Hansulrich Obrist

The smaller chunks you break the velocity calculation up into, the more information you can get about events during the total movement of the object, or the more detailed the available information becomes. Over chunks of intervals, the measured velocity is said to be “instantaneous velocity”. Instantaneous velocity is essentially the velocity of the object at a particular point in time or the average velocity at a specific instance. The speedometer of a car shows the car’s magnitude, the rate of change (not the direction of the change). To make this difference more explicit: When a police officer pulls a car over, the officer will use the car’s instantaneous velocity to give a ticket, but when you are trying to calculate how long it will take you to traverse between two different cities you want to use average velocity.

Let’s look at one more example:

If a car is driving a course of 1000 meters and it reaches its endpoint traveling at top speed in a time frame of 1 minute and 20 seconds (80 seconds), what would be the velocity of the vehicle? The vehicle’s velocity could be calculated like this:

Vavg = (Xf – Xi)/t = Δx/t
or…
Vavg = 1000m – 0.00m/80.0s (where the track’s endpoint is 1000m).
Vavg = 1000m/80.s
Vavg = 12.5m/s

Therefore, the car’s velocity is 12.5m/s.

Difference Between Velocity And Speed

Photo: LoggaWiggler via Pixabay, CC0

Most people use the term velocity as if it were equivalent to the term speed, so colloquially the terms are used interchangeably. Yet you should be aware that in the realm of physics speed and velocity are two distinct things with their own meanings. One of the primary differences between velocity and speed is that while velocity has direction, speed doesn’t. Speed is only a scalar value, a variable with only one value at a time.

Much like there is a difference between average velocity and instantaneous velocity, there is also a difference between average speed and instantaneous speed. Instantaneous speed can be thought of as equivalent to the magnitude of the instantaneous velocity. So while a velocity could be negative relative to the starting point of an object, as in the -4.0 m/5s example above, the instantaneous speed would be a positive 4.0 m/5s.

“The energy varies with the square of the velocity, so if you need five times the velocity, that’s 25 times the energy.” — Buzz Aldrin

Here’s another illustration:

For a given instant during a car trip, your instantaneous velocity is 55 km/hr due west. The instantaneous speed for this instantaneous velocity would be 55km/hr, the exact same magnitude or rate of change, yet there would be no direction. If that’s the definition of instantaneous speed, what is the definition of average speed?

Average speed would be the total distance an object has traveled divided by the time needed to travel the distance. This means that while the magnitude of instantaneous speed and velocity will always be the same, there could be substantial differences in the magnitude of the average velocity and the magnitude of the average speed.

To Sum Up:

The basic definition of average velocity is: Vavg = Δx/Δt = Xf – X0/tf – t0

This is the change in position divided by the time of travel.

You should know that the velocity/time equation is just one important equation using velocity, but others exist. The position-time equation (s = s0 + v̅t [a]) is for figuring out where an object is likely to come to rest given its velocity and starting position over a given time.