What Is cos(0) Equal To?

In mathematics, the cosine function (cos) is a function that relates the interior angle of a triangle to the length of its sides. The cosine function, along with the sine and tangent function are the three basic trigonometric functions. In a right triangle, the cosine of an angle is equal to the ratio of the side adjacent to the angle to the length of the hypotenuse of the right triangle. Mathematically, this is:

cos(A) = adjacent/hypotenuse

The cosine function takes angle measurements as its input and returns a ratio as its output. When the angle A=0° then the cosine function takes on the value:

cos(0) = 1

The cosine of a zero degree angle is equal to 1. To see why consider what happens to a right triangle as one of its angles tends towards 0. As the angle approaches 0, the opposite side gets smaller and smaller. As this angle gets smaller, the lengths of the hypotenuse and side adjacent to the angle get closer and closer. Once the angle measurement hits 0, the hypotenuse and the adjacent side will lie perfectly on top of each other, falling into a 1-to-1 ratio. Thus, the cosine of 0 is equal to 1.

Basics Of Trig Functions

The three trig functions represent a general correspondence between the interior angles of a triangle and the lengths of its sides. The fact that there is a repeating relationship between the sides and angles of a right triangle is a consequence of the fact that similar triangles maintain ratios between their sides. A 3-4-5 right triangle has the same proportions as a 6-8-10 triangle; the latter is just an integer multiple of the former. So, any ratios between the lengths of the sides of the two triangles will be exactly the same.

Consider a simple right triangle:

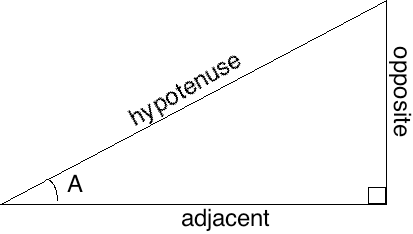
Credit: D Pape via Resumbrae CC-BY 2.0

Starting with some angle A, the sides of the triangle are labeled as follows:

The hypotenuse is the side opposite the right angle. The hypotenuse is always the longest side in the triangle.

The opposite side is the side directly across from the angle of interest.

The adjacent side is the one directly next to the angle that is not the hypotenuse.

Following these designations, we can define the three main trig function as follows:

sin(A) = opposite/hypotenuse

cos(A) = adjacent/hypotenuse

tan(A) = opposite/adjacent

Because similar triangles have the same proportions, the values of these functions are not dependent on the size of the right triangle, only that the angle of evaluation (A) is equal. A nice mnemonic for remembering the definitions of trig functions is the acronym SOH-CAH-TOA (pronounced “so-kah-toa”)

Lets put some numbers to these abstract formulas. Say we have a right triangle with side lengths of 3 and 4 and a hypotenuse of length 5:

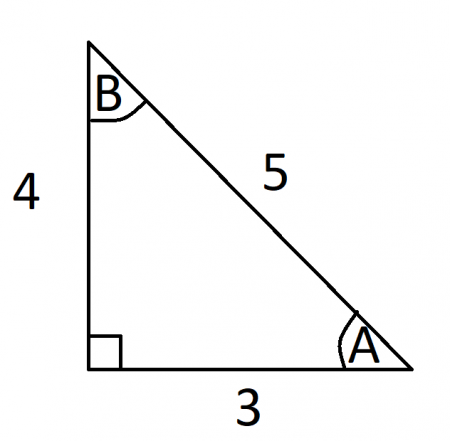
Credit: Author

We can compute the values of the trig functions with respect to angle A as follows:

sin(A) = opposite/hypotenuse = 4/5 = 0.8

cos(A) = adjacent/hypotenuse = 3/5 = 0.6

tan(A) = opposite/adjacent = 4/3 = 1.3

Notice that the sine and cosine functions are equivalent taking different angles into consideration. Setting angle B as our angle of interest, we can compute the trig functions as follows:

sin(B) = 3/5 = cos(A) = 0.6

cos(B) = 4/5 = sin(A) = 0.8

This leads us to the general rule that, for any right triangle where angles A and B are not the right angle:

sin (A) = cos(B) and sin(B) = cos(A)

In addition to the 3 basic trig functions are the 3 reciprocal trig functions. The reciprocal functions are the reciprocals of the basic functions and are called secant, cosecant, and cotangent. They can be defined as:

sec(A) = 1/sin(A) = hypotenuse/opposite

cosec(A) = 1/cos(A) = hypotenuse/adjacent

cotan(A) = 1/tan(A) = adjacent/opposite

Numerical Values Of Trig Functions

Say you are given just an angle measurement and you are asked to compute the sine of that angle just from that value. Unfortunately, there is no simple algorithm to do this. Computing sin values by hand from a given angle take a lot of time and complex calculations. Instead, most calculators use lookup tables, tables that have a list of angle measurement and the corresponding sin values. These tables have been calculated to an extreme amount of precision. However, there is an interesting way of conceptualizing angle measurements that makes calculating some values of the trig functions intuitive and easy.

Trig Functions And The Unit Circle

The inner workings of trig functions can be understood with respect to the structure of the unit circle on the coordinate plane. A unit circle is a circle with radius one that is centered on the origin of the coordinate plane (0,0). Dragging the radius around the origin point will trace out a circle whose circumference is exactly 2π units in length. By the Pythagorean theorem, this circle is the set of all points (x, y) such that x²+y²=1

Angles can be measured in terms of the length of the arc on the circle that the angle traces out. These units are called radians. Since the unit circle has a circumference of exactly 2π, a radian angle measure of 2π corresponds to 360°. Likewise, π/2 radians corresponds to 90°, π radians to 180°, π/3 radians to 60°, and so on

The unit circle and the conversions between radians and degrees. Credit: Gustav B via WikiCommons CC BY-SA 3.0

Any point on the unit circle can be represented as the endpoint of a line extending from the center point with an angle θ centered on the origin. The x and y values of that point correspond to the sides of the right triangle. This understanding leads to some interesting properties of the trig functions. Since by definition, the unit circle has a radius 1, sin(θ) = y and cos(θ) = x. By the Pythagorean theorem and the definition of a unit circle, it is true that cos²(θ) + sin²(θ) = 1.

What happens to the right triangle if we change the angle of the ray from the origin? Changing the angle that the line extends from the origin causes the other sides of the triangle to change accordingly. As we make the angle smaller, the side opposite from the angle also gets smaller. and the adjacent side gets larger. As we make the angle larger, the opposite side gets larger and the adjacent side gets smaller. So as we change the angle, we can visualize how the ratio of the sides of the triangle change.

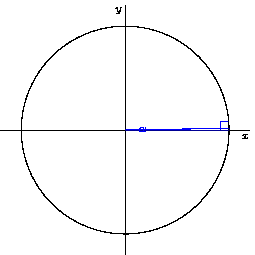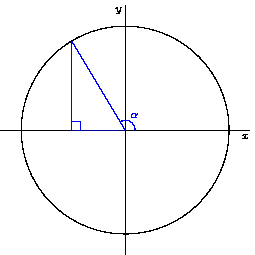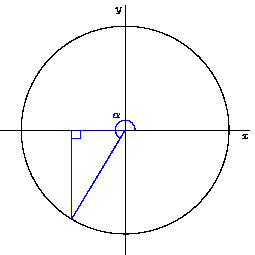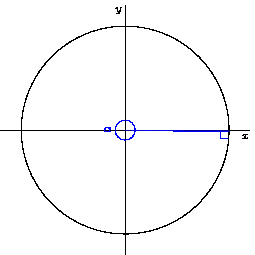
An animation showing how the sides of the triangle change in response to changing the angle. Credit: WikiCommons CC0 1.0

Notice immediately a few things. What happens when the angle is 0? What are the ratios of the sides to each other? As the angle approaches 0, the sine of the angle (opposite/hypotenuse) gets smaller and smaller. When the angle hits 0, the length of the opposite side hits 0, so the entire ratio between the opposite side and hypotenuse is 0. So, we know that sin(0) = 0. 

What about when we make the angle larger? As we make the angle larger, the opposite side increases in length, until we get to π/2 rads (90°), at which point the opposite side and the hypotenuse become equal length. If the sides are equal length, then their ratio is 1, so we know that sin(π/2) = 1.

Consider the cosine function. What happens to the value of the cosine as the angle gets smaller? As it approaches 0, the ratio between the adjacent side and the hypotenuse gets larger, until the adjacent side and hypotenuse are equal when the angle is 0. So we know that cos(0) = 1. Likewise, as the angle approaches π/2, the adjacent side gets smaller and smaller with respect to the hypotenuse until it becomes 0; thus, cos(π/2) = 0

What about the tangent function? When the angle is 0, the ratio of the opposite side to the adjacent side is also 0, so we can determine that tan(0) = 0. As the angle increase, the opposite side gets larger and the adjacent side gets smaller until it reaches a point where the two sides are the same length. A right triangle can only have two sides that are equal in length when the non-right angles are both 45° angles. This means that at a 45° angle, the lengths of the two sides are equal, and so their ratio is 1. 45° is equal to π/4 rads, so we know that tan(π/4) = 1

What about the value of tan(π/2)? Notice that as the angle gets larger and approaches π/2 rads, the opposite side gets larger and the adjacent side shrinks to 0. This means that tan(π/2) is equal to the expression 1/0. Division by 0 is undefined, so the function tan(π/2) is undefined and has no accepted value.

Conceptualizing angle measurements in terms of radians of a unit circle also explains another interesting property of the trig function; their periodicity. The values of the trig functions oscillate between fixed outputs from inputs 0 to 2π because angle measurements greater than 2π can be represented as multiples 2π. Graphing the output of the sin and cosine functions produces a nice lofty wave-like pattern:

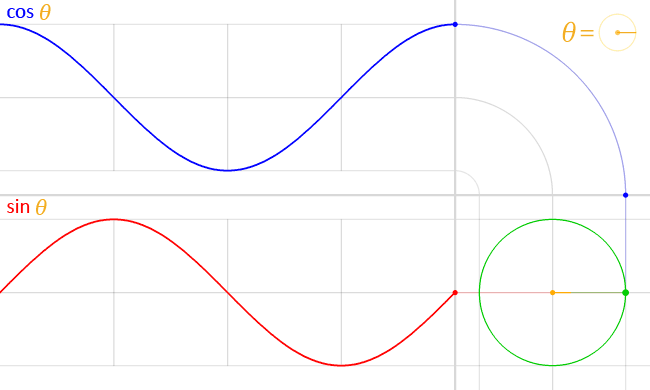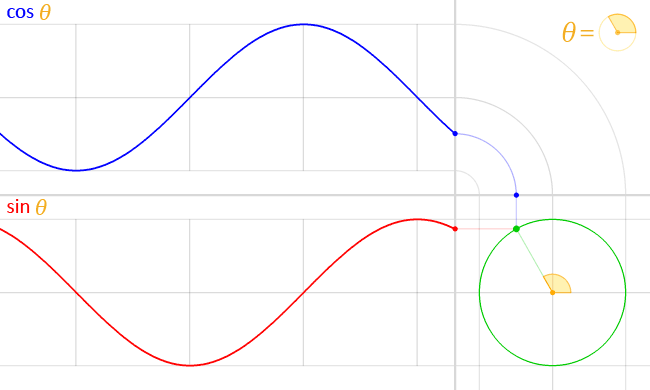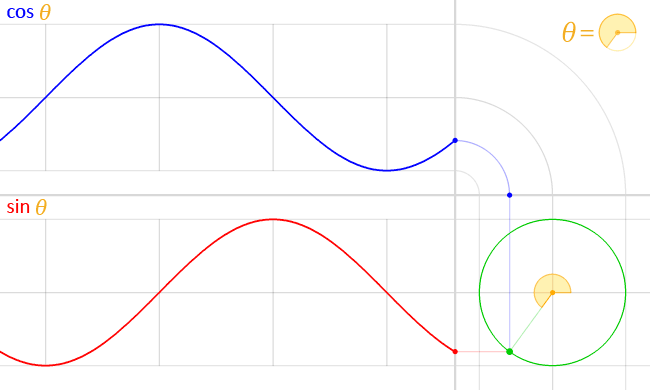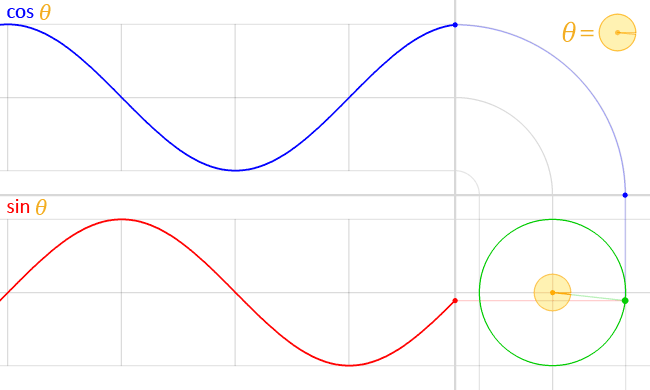
Credit: WikiCommons CC0 1.0

The crests and troughs of the above graphs represent output values of 1 and -1 respectively. It is interesting to note that the sine and cosine function are identical in form, but that the cosine function is offset from the sine function by half a wavelength. The periodicity of the trig function (sine and cosine in particular) make them useful in science for modeling periodic phenomena like mechanical or electromagnetic waves.