Arc Length Formula (Equation) With Examples

The arc length of a circle refers to the measure of the length of a curve on the outside of a circle. The general formulas for calculating the arc length of a section of a circle are:

• s = 2πr(θ/360), when θ is measured in degrees,

and:

• s = rθ, when θ is measured in radians

“Life is full of circles.” — Nora Roberts

Where s is the arc length and r is the radius of the circle. Recall that 2πr is equal to the circumference of the circle, so one can see the above equation as reducing the entire circumference by the ratio of the central angle θ to a full rotation of 360°.

Degrees and Radians

Strictly speaking, there are actually 2 formulas to determine the arc length: one that uses degrees and one that uses radians. Typically, the interior angle of a circle is measured in degrees, but sometimes angles are measured in radians (rad). In a unit circle, the measure of an arc length is numerically equal to the measurement in radians of the angle that the arc length subtends. So, the measure of an angle in radians can be thought of as telling you how many radii of the circle could fit in the arc traced out by the angle. So an angle of 1 rad subtends an arc length equal to one radius.

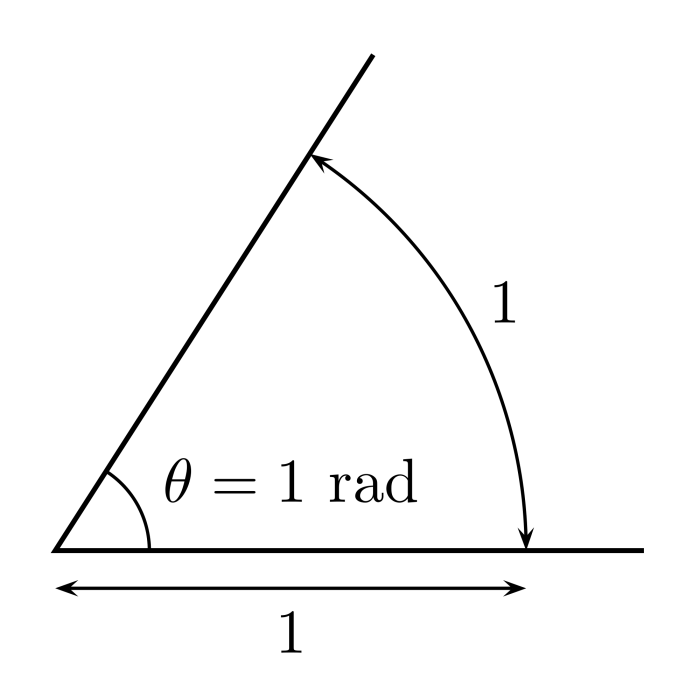
The definition of 1 radian. Source: “Angle radian” by Gustavb via WikiCommons licensed under CC-BY-SA 3.0

Often times, mathematical problems will ask you to convert an angle measure from degrees to radians as radians are mathematically simpler to work with. First, we can note that an angle of 2π rad is equal to 360°. This is because there are 2π radii in the full circumference in a circle. Therefore, an angle of 2π rad would trace out an arc length equal to the circumference of the circle, which would be exactly equal to an arc length traced out by an angle of 360°. With similar reasoning, we can determine that an angle of π rad must be equal to a 180° angle. The general formula for converting degrees to radians is:

• rad = θ(π/180)

So we can determine that a 30° angle is equal to 30π/180 = π/6. By simply dividing both sides by (π/180) we can get the formula for converting rads to degrees:

• θ = rad(180/π)

So we can figure out that 4π/9 rad is equal to (4π*180)/9π = 720π/9π = 80°. Converting angle values from degrees to radians and vice versa is an integral part of trigonometry.

“Circles, like the soul, are neverending and turn round and round without a stop.” — Ralph Waldo Emerson

Sample Problems

Now that we have clarified the relationship between degrees and radians, we have 4 major formulas to use, the two arc length formulas:

• s = 2πr(θ/360)
• s = rθ

and the two conversion formulas:

• rad = θ(π/180)
• θ = rad(180/π)

Let’s examine some practice problems for getting a handle on these equations.

(1)

Question: A circle has a radius of r=12 meters. What is the length of an arc traced out by a 60° angle in the center of the circle?

Answer: in this problem, we know both the central angle (60°) and the radius of the circle (12). All we have to do is plug those values into our equation and we get:

• s = 2π(12)(60/360)
• s = 24π/6
• s = 4π

So the length of an arc traced out by a 60° angle in a circle with a radius of 12 meters equals 4π meters ≈ 12.57 meters.

(2)

Question: A circle has an area of 72π square meters. What is the length of the arc traced out by a center angle of π/8 radians?

Answer: We are given the area of a circle (72π) and the angle measured in radians (π/8). The area of a circle is equal to 2πr² so we can determine the radius of the circle by working backward:

• 72π = 2πr²
• 36 = r²
• 6 = r

Therefore, the radius of the circle equals 6 meters. Plugging the values into our equation for arc length gives us:

• s = 6(π/8) = 3π/4

So the length of the arc traced out by an angle of π/8 rad in a circle with an area of 72 equals 3π/4 meters ≈ 2.36 meters.

(3)

Question: Jeremey cuts out a slice from a circular pizza that has a crust length of 4 inches. Considering that the circular pizza has a radius of 8 inches, how big of an angle in degrees is the hole Jeremy’s slice left?

Answer: In this case, we know the arc length (4) and the radius of the circle (8). Plugging these values into our equation yields:

• 4 = 2π(8)(θ/360)
• 1/4 = πθ/360
• 90 = πθ
• θ = 90/π

The slice left a cutout with an angle of 90/π° ≈ 28.65°.

Arc Sector Formula

The arc sector of a circle refers to the area of the section of a circle traced out by an interior angle, two radii that extend from that angle, and the corresponding arc on the exterior of the circle. In order to find the area of an arc sector, we use the formula:

• A = r²θ/2, when θ is measured in radians, and
• A = (θ/360)πr² when θ is measured in degrees.

The arc sector formula is useful for determining partial areas of a circle. Let us examine a sample problem to see an application of the arc sector formula.

“Love is like pi: natural, irrational, and very important.” — Lisa Hoffman

(4)

Question: Annie and Bob have joined a new circular farming commune. The circular farm has a radius of 7 miles. Annie and Bob have been put in charge an arc sector of the land. They know that the arc length of their sector is 2 miles. What is the total area of the land that Annie and Bob are in charge of?

Answer: This question requires two steps. First, we must determine what the measure of the angle that subtends their sector. Then we can use that value to determine the whole area of the arc sector. We know that the arc length of their sector is 2 miles, and we know the radius of the circular farm is 7 miles. We can figure out the angle in radians by:

• 2 = (7)θ
• θ = 2/7 rad

The angle of their arc sector in radians is 2/7 rad, so we can now use the value to determine the total area of their arc sector:

• A = (5²(2/7))/2
• A = 5²/7
• A = 25/7

The total area of Annie and Bob’s sector is 25/7 miles² ≈ 3.57 miles².

So, in summation The formula for arc length is:

• s = 2πr(θ/360), when θ is measured in degrees,

and:

• s = rθ, when θ is measured in radians.

The corresponding formulas for arc sector are:

• A = r²θ/2, when θ is measured in radians,

and

• A = (θ/360)πr² when θ is measured in degrees.