Algebra Formulas: Cheat Sheet

Do you remember the quadratic formula? How about the equation of a circle? What about the formula for exponents and logarithms? Odds are you have heard of these mathematical concepts but cannot pull the formulas off the top of your head. Luckily for you, that’s why we are here!

Here is a cheat sheet with a number of common algebraic formulas that you might find in your math classes. Afterward, we will look at some specific examples of how to use these formulas.

Algebraic Formula Cheat Sheet:

Arithmetic Operations

Addition

when c ≠ 0

 when b, d ≠ 0

Multiplication

 when b, d ≠ 0

Division

 when b, c ≠ 0

 when a, c ≠ 0

 when a, b, c, d ≠ 0

Exponent Rules

Radical Rules

Distance Formula

For two points P₁ = (x₁, y₁) and P₂ = (x₂, y₂) on a coordinate plane, the distance between the two points is given by the formula:

Quadratics

For equation in the general quadratic form ax²+bx+c=0 where a ≠ 0:

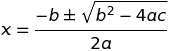
If (b²−4ac) > 0 – two real solutions,

if (b²−4ac) = 0 – one real solutions,

if (b²−4ac) < 0 – two complex solutions

Functions And Graphs

Linear Equations

For a line with slope m and crossing through the point (0, b), the equation of the line is:

For 2 points P₁ = (x₁, y₁) and P₂ = (x₂, y₂), the slope of a line through those points can be calculated as:

The equation of a line with slope m crossing through point P = (x₁, y₁):

(“Point-Slope” form)

Parabolas

The general equation for a parabola with a vertex at point (h, k) is:

If a > 0, then the parabola points up

If a < 0, then parabola points down

Circles

The general equation for a circle with radius r and center point (h, k) is:

Logarithms

ex): log₅ 125 = 3 because 5³ = 125

 when e = 2.718281828…

Sample Problems Using Equations

Q1.) A farmer is laying out a fence for his field. Beginning from one corner, he drags a line 7 units to the right, then 12 units up. How far away from the starting point is he?

Answer: We can interpret this problem by visualizing the fence on a coordinate plane. If the farmer begins at the origin (0,0), goes 7 units right then 12 units up, he ends at the point (7, 12). All we need to do is compute the distance between the distance between points (0, 0) and (7, 12). Using the distance formula we get:

D = √(7−0)²+(12−0)²

D = √(49+144)

D = √193

D ≈ 13.89

The farmer will be 13.89 units from the starting point.

Q2.) The equation of motion for a projectile accelerated in the air with respect to time t is given by the quadratic expression:

y = −16t²+32t+128

Assuming that air resistance is negligible, how long will it take the projectile to hit the ground?

Answer: We can solve this one with a bit of geometric visualization. The equation y = −16t²+32t+128 takes on the shape of a parabola facing downwards. If the ground is considered y=0, then we want to solve for t when −16t²+32t+128 = 0. This expression is in quadratic form (ax²+bx+c=0) so we can solve for t by using the quadratic equation like so:

t = (−32±√(32²−4(-16)(128)))/2(-16)

t = (−32±√(9261))/−32

t = (−32±96)/−32

t = 64/−32 and t = −128/−32

t = −2 and t = 4

In our example, a time of −2 seconds does not make physical sense, so the correct answer is t = 4. The projectile will hit the ground in 4 seconds.

Q3.) A line with a slope of 4 runs through the point (1, 7). What is the equation of the line?

Answer: Recall that the general formula for a line is y = mx+b. We are given the slope of the line (4) and a point the line crosses through (1, 7). We need to reverse engineer the linear equation from these two pieces of information.

Luckily we have an equation for that. The point-slope formula allows us to reconstruct the equation of a line from information about its slope and a single point. Using the formula we get:

y = 7+4(x−1)

y = 7+4x+−4

y = 4x+3

The equation of the line is y = 4x+3.

Q4.) Link and Zelda are enjoying some Hylian shroom pizza. If Link eats two-sevenths of the pizza and Zelda eats one fifth, how much in total did they eat?

Answer: All we need to do here is add the fractions 2/7 and 1/5. Using the formula above

2/7 + 1/5 = 2(5)+7(1)/(7)(5)

= 17/35

All together they ate 17/35ths of the pizza.

Q5.) You are experimenting with cells in the lab to see how they divide. In your experiment, you discover that starting with one cell, the population of the cells doubles every minute. 1) Write an equation describing the growth of the cells with respect to time and 2) determine how long it would take for the number of cells to reach 100,000.

Answer: This one is a bit tricky and requires us to work with exponents and logarithms. First, we are asked to make an equation describing the rate of growth of cells over time. If we graphed our findings, on a coordinate plane, our points would be (time, number of cells). When t=0 there is one cell (0, 1). When t=1, there are 2 cells (1, 2). At t=2 there are 4 cells (2, 4). At t=3 there are 8 cells (3, 8).

This pattern hints at an exponential relationship between the pairs of points. 2⁰=1, 2¹=2, 2²=4, 2³=8, etc. Therefore, our formula to estimate the number of cells after t minutes is:

number of cells = 2^t. 

Next, we are asked to figure out how long it would take for the number of cells to reach 100,000. Setting our formula equal to 100,000 gives us:

100,000 = 2^t

We can solve this one using logs and their interesting properties. Take the natural log of both sides:

ln(100,000) = ln(2^t)

Using the log power rule, we can bring down t and divide to solve:

ln(100,000) = ln(2^t)

ln(100,000) = t ln(2)

ln(100,000)/ln(2) = t

t ≈ 16.61 minutes

At a rate of doubling every minute, it would take 1 cell about 16.61 minutes to divide into 100,000 cells.

Q6.) Shmoop is a dog that really likes pineapples. Over the last 4 weeks, Shmoop has gathered 3⁴ pineapples. Assuming the rate stays constant, how many pineapples will Shmoop have after 108 weeks?

Answer: This problem requires us to multiply powers. First, we need to find a factor that relates the total amount of pineapples gathered to weeks passed. Every 4 weeks, Shmoop gather 3⁴ pineapples. Dividing 108 by 4 gives us

108/4 = 27

27 can be represented as a power of 3 (3³). Now we just have to multiply 3³ by 3⁴ to get:

3³ × 3⁴  = 3⁷

3⁷ = 2187 pineapples

Shmoop sure is a busy dog. After 108 they will have gathered 2187 pineapples.

Q7.) “Loudness” is measured in decibels (dB). The formula for decibels is

dB = 10log[I ÷ I₀]

where I₀ is the “threshold intensity”—the lowest intensity sound that can be perceived. The intensity of other sounds is defined as integer multiples of the threshold intensity. (ex. cat purr = 326 I₀, 25 dB)

Considering that exposure to sounds louder than 85 dB can damage the ears and considering that a .22 rifle fires with an intensity of I = 2.5×10¹³ I₀, should a person wear ear protection at the shooting range?

Answer: Evaluating this situation using the formula for decibels gives us:

dB rifle = 10log[2.5×10¹³ I₀÷ I₀]

dB = 10log[2.5×10¹³]

dB ≈ 134

134 dB is very high above the threshold to cause ear damage, so yes, a person should wear ear protection at the shooting range.

Q.8) The escape velocity V_E for a planet is given by the equation

V_E = √(2Gm/r)

Where G is the gravitational constant, m is the mass of the planet, and r is the radius of the planet. Earth has a mass m = 5.98 × 10²⁴ kg, a radius r = 6.38 × 10⁶ m  and a gravitational constant G = 6.67 × 10⁻¹¹. Calculate the escape velocity of Earth.

Answer: This problem looks difficult only because of the large numbers. all we have to do is plug in and crunch the numbers, being careful with the units and scientific notation:

V_{E Earth}= √((2× 6.67 × 10⁻¹¹ × 5.98 × 10²⁴)/ 6.38 × 10⁶)

= 11,200 m/s

= 11.2 km/s

The escape velocity for Earth is about 11.2 kilometers per second

Q.9) Two spinners with 12 numbered spots are spun. Assuming that each spinner is equally likely to fall on each space, what is the probability that the two spinners will both land on the same number? What is the probability that their will both land on a number greater than 4?

Answer: This problem has us dealing with fractions and probabilities. It asks us to find the probability of two independent events both occurring. Starting with the first spinner, since there are 12 spaces and the spinner is equally likely to fall on each one, the probability for a given space is just 1/12. Likewise for the second spinner. The probability for the conjunction of the events is just the product of the probability of each event:

Pr = (1/12) × (1/12)

Pr = 1/144

That is, there is a 1/144 chance that both spinners will land on the same spot.

What about the second part of the question? What is the probability that both spinners will land on a number greater than 4? Using the same logic, we know that the probability of the first spinner landing on a number greater than 4 is 8/12=2/3. The probability that the other spinner will land on a number greater than 4 is also 8/12=2/3.

Therefore, the probability of both spinners landing on a number greater than 4 is:

2/3 × 2/3 = 4/9

Q10.) Does the point (3, 4) fall on a circle with a center of (0, 0) a radius r = 5?

Answer: Since we know the general equation of a circle, we can plug in these values to see if they satisfy the equation.

5² = (3−0)² + (4−0)²

25 = 9 + 16

25 = 25

The answer is Yes, the point (3, 4) exists on a circle with a center (0, 0) and a radius r = 5.