
If you’re wondering what an antilog is and how to calculate it, you actually probably already know a little about antilogs. Antilogs are just another term for exponents. You can think of an antilog as being the inverse of a logarithm, and to calculate the antilog, you’ll just invert the regular logarithm you have.
Let’s take a closer look at antilogs and how they relate to exponents and logarithms.
Since it is difficult to discuss something without a common definition of the terms involved, let’s start out by defining all of our terms.
Definition of Exponents
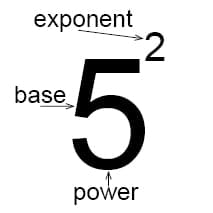
Photo: MathPlanet, CC-BY 4.0
Exponents are just shorthand/stand for the repeated multiplication of a variable by itself. When we speak of something being to the “Nth power” (N standing in for any number), we mean that number/variable is being multiplied by itself that many times. For instance, 4^4 means 4 to the fourth power, or 4 x 4 x 4 x 4. Remember that the term “raising to a power” just means multiplying a given variable by itself to the specified number of times.
A Note On Squaring and Cubing
There are specific terms for exponents that multiply something by itself once and those that multiply something by itself twice. Multiplying a value by itself is known as “squaring” something, represented as Y^2 or Y to the second power. Multiplying something by itself twice (Y x Y x Y) is known as cubing something, or raising it to the third power.
Inverse Functions
An inverse function means taking a function (such as an exponent) and doing the inverse of it. So if the given function A take X as an input and gives an output of Y, the function A^-1 (the negative denoting the inverse), would take Y as an input and give X as an output.
The Relationship Between Exponents And Logarithms
Photo: geralt via Pixabay, CC0
Remember that exponents are just the inverse function of a logarithm, and logarithms the inverse function of exponents. Knowing this, you might guess that Inverse Log or AntiLog is just another term for exponents. Logarithms, therefore, are just another way to conceive of exponents. If you know that 8 to the second power, or eight squared equals 64, you can represent that as: 8^2 = 64.
Yet as a logarithm, the variable you are trying to find is the exponent, so you are attempting to find the exponent as the missing value. Here’s an example question: 8 raised to some power (X) equals 64. You can express this question with the logarithmic equation: log8(64) = 2. So to make this comparison explicit: log8(64) = 2 is just the inverse of 8^2 = 64. Logarithms and exponents work with the same basic variables, the primary difference is that logarithms isolate the exponent while exponential equations isolate the power. Knowing this, it’s easy to see why a logarithm’s base will be exactly the same as an exponent’s base.
Now that we have gone over all the definitions, let’s look at an example of converting logs to antilogs(exponents). If log(10)100 = 2, then the conversion is quite easy, just swap the position of the middle and end values to get antilog. So the antilog is: Antilog(10) 2 = 100. Now to express this as an exponent formula, just make the 2 an exponent: 10^2 = 100.
Examples Of Converting Between Logs And Antilogs
Let’s take a look at some examples of converting between antilogs and logs.
If given the logarithmic expression log2(⅛) = -3: The equivalent exponential form is 1 / 8 = 2^-3
If given the logarithmic expresssion log3(27) = 3: The equivalent exponential form is 27 = 3^3
If given the logarithmic expression log36(6) = ½: The equivalent exponential form is 6 = 36^1/2
If given the logarithmic expression log8(2) = ⅓: The equivalent exponential form is 1 / 8 = 2^-3
The Use Of Antilogs
When calculations were still done with slide rules, instead of calculators, it was more common to see the term antilog used. Most people nowadays will use the term exponent instead of antilog, largely because of the fact that computers now perform most calculations for us. The term antilog is primarily used in the field of electronics, in reference to electrical circuits and the operators/amplifiers that affect the flow/output of a circuit.
An amplifier is an electrical device that is capable of altering/increasing the power, current, or voltage of a signal. Amplifiers increase the magnitude of a signal. Different sizes and types of amplifiers are used to carry out different tasks. Smaller, weaker amplifiers are usually used in wireless receivers and to amplify sound in CD players and headsets. Power amplifiers are often used in broadcasting transmitters, wireless transmitters, and hi-fi audio devices.
Logarithmic amplifiers are nodes found in a circuit where the output to a terminal needs to be altered. A logarithmic electrical amplifier will produce an output that is scaled in proportion to the input log of the signal. The input terminal takes in the signal, the amplifier alters it and then the signal is sent out to the next terminal.
As you might guess, an antilog amplifier operates very similarly to a logarithmic amplifier, just inverting the signal. An antilog amplifier would take the output signal and run it, with negative feedback, to the inverting terminal.
To Sum Up:
Antilogs are just another term for exponents, and exponents are the inverse of logarithms. When you want to convert between logarithms and antilogs, swap the position of the middle and end values to get antilog. So now you know that antilogs are the same thing as exponents, and that exponents are just the inverse of logarithmic functions. As long as you know how to convert between exponents and logarithms, you’ll be fine.








