What is the hardest math problem in the world? The answer to that question is tricky. “Difficulty” is a subjective metric and what is difficult for some may not be difficult for others. Some math problems, such as the infamous question 6 of the 1988 Math Olympiad are easy to understand but monstrously complex to solve. Others such as the 7 Bridges of Königsberg problem seem complex but have a deceptively simple answer.
A reasonable metric to determine how “difficult” a math problem is could be the number of people that have solved it. Therefore, it stands to reason that the hardest math problems in the world are ones that no mathematician has solved yet. With that in mind, we are going to take a look at 6 of the most difficult unsolved math problems in the world.
1.Goldbach Conjecture
Let’s start our list with an extremely famous and easy-to-understand problem. First, take all the even natural numbers greater than 2 (e.g. 4, 6, 8, 10, 12…). Next, take each even number and try to rewrite it as the sum of 2 prime numbers. For our first 5 elements of our list, we get:
4 = 2+2
6 = 3+3
8 = 3+5
10 = 3+7 = 5+5
12 = 7+5
…
100 = 3+97 = 11+89
The question is, can you keep doing this forever? That is, can you write every possible even natural number as the sum of two primes? The Goldbach conjecture answers this question in the affirmative. It states:
GB: “Every even integer greater than 4 can be written as the sum of two prime numbers.”
The Goldbach conjecture was first proposed by German mathematician Christian Goldbach in 1742, who posited the conjecture in correspondence with Leonhard Euler.

The first 50 even numbers written as the sum of two primes. Credit: A. Cunningham via WikiCommons, CC-BY SA 3.0
To date, the Goldbach conjecture has been verified for all even integers up to 4 × 1018 but an analytic proof still eludes mathematician. Although mathematicians do not have a rigorous proof yet, the general consensus is that the conjecture is true. The informal justification for this claim comes from the nature of the distribution of prime numbers. In general, the larger an integer is, the more likely it can be expressed as the sum of two numbers. Therefore, the larger an integer is, the more likely that at least one of these combinations will consist of only primes.
2. Inscribed Square Problem
Take a pencil and draw a closed curve. The curve can have as many squiggles and bends as you want; the only conditions are that you have to close it end-to-end and it cannot intersect itself. Next, try to find some 4 points located on the curve such that you can draw a square using those points. Can you do it?
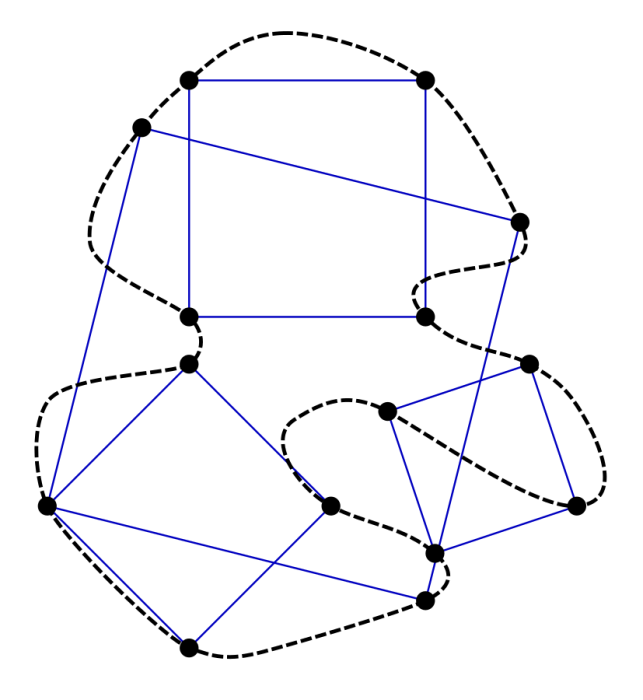
The inscribed square problem concerns whether or not any generic closed non-intersecting curve contains the 4 points of a square. Credit: C Rocchini via WikiCommons CC-BY SA 3.0
This is known as the inscribed square problem. The inscribed square problem asks whether every possible closed non-intersecting curve contains the 4 points of a square. The inscribed square theorem has been proven for a number of special cases of curves. For example, it has been proven that circles and squares have an infinite amount of inscribable squares, obtuse triangles have exactly one, while right and acute triangles have exactly 2 and 3 respectively. The theorem has not been proven for the general case of any closed curve though.
3. Continuum Hypothesis
Modern math has infinities all over the place. There are infinite positive whole numbers (1,2,3,4…) and an infinite amount of lines, triangles, spheres, cubes, polygons, and so on. Modern math has also proven that there are different magnitudes of infinity as well. We say a set of elements is countably infinite if the elements of that set can be put into a 1-to-1 correspondence with the positive whole numbers. So the set of whole numbers is a countable infinite and so is the set of all rational numbers.
In the 19th century, Georg Cantor discovered that the set of real numbers is uncountable. This means that if we tried to go through and assign a positive whole number to every real number, we would never be able to do it, even if we used all the whole numbers. Thus, uncountable infinities can be considered “bigger” than countable infinities.
The continuum hypothesis asks whether or not there exists a set of numbers that is an infinity whose magnitude is strictly between countably and uncountably infinite. The continuum hypothesis is a bit different than other problems on this list because, not only has it not been solved, it has been proven to be unsolvable, or at least, unsolvable using current mathematical techniques. This means that, while we do not know the truth of the continuum hypothesis, we know that it can neither be proven nor disproven using the resources of modern set theory. Solving the continuum hypothesis would require a new framework for set theory, one which has not been created yet.
4. Collatz Conjecture
First, pick any positive number n. Next, construct a sequence from the previous number as follows: if the number is even, divide by 2. If it is odd, multiply by 3 and add 1. The goal is to repeat this sequence until you get the number 1. For example, let’s try this sequence with the number 12. Beginning with 12, we get:
12, 6, 3, 10, 5, 16, 8, 4, 2, 1
If we start at 19, we get:
19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1
The Collatz conjecture states that no matter what value of n you begin with, this sequence will always eventually terminate in 1. Currently, this conjecture has been checked for all values of n up to 87 × 260 but so far no proof exists.
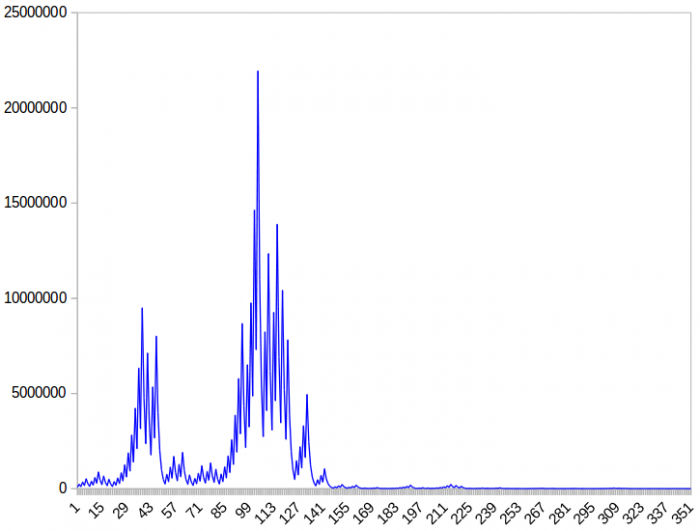
A graph showing the number of iterations of the procedure required for specific numbers. Credit: J. Arantes via WikiCommons CC-BY SA 4.0
The Collatz conjecture is interesting because it is very easy to describe and understand, but so far no one has even come close to cracking it. Even the extraordinarily famous mathematician Paul Erdős who was known for cracking unsolved problems in math once stated in regards to the Collatz conjecture that, “Mathematics may not be ready for such problems.”
5. Solving Chess
In game theory, an optimal strategy refers to a finite sequence of steps such that following those steps always results in winning the game. Mathematicians have found optimal strategies for games like connect-4 or tic tac toe; a set of moves one can take so that that they will always win.
For quite a while, mathematicians have been looking for an optimal strategy for chess; that is, a set of steps one could take to ensure they will always win a game of chess. The particular problem of solving chess in interesting becaue, while we know for certain that such an optimal strategy exists, it is likely that we will never find it. This is simply because of the enormous complexity of chess.
Consider the problem this way; any program that can solve chess would have to be able to compare all possible variations of a game of chess to find the optimal move. For every move taken in chess, the number of possible games increases exponentially. Just take a look at the following table:
|
No. of moves (ply) |
No. of possible games |
|
1 |
20 |
|
2 |
400 |
|
3 |
8,902 |
|
4 |
197,281 |
|
5 |
4,865,609 |
|
6 |
119,060,324 |
As the number of moves increases, the number of possible games grows extremely quickly. After just 5 moves (10-ply in chess terminology) the number of possible games is over 69 trillion. It is estimated that the total number of possible positions on the chess board is somewhere on the order of 10^120 (a number called the Shannon number). This means that if a computer were to go through and check every possible position of chess, it would take about 10^90 years, about 8.3 x 10^79 times the current age of the universe (13 billion years). Given these computational limitations, it seems unlikely that we will ever solve chess, at least using current computing techniques.
It is true that scientists have managed to create AIs that play chess better than world-ranked champions, but so far none of these AI work by solving the game of chess. They instead work by combing through terabytes of data to look for winning chess strategies.
6. The Riemann Hypothesis
The Riemann hypothesis is considered by many to be the single most important unsolved problem in mathematics. The Riemann hypothesis concerns the roots of the Riemann zeta function, which is defined for all complex numbers s with a real part greater than 1 by the convergent series:
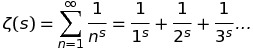
It is known that when s is some negative even integer (-2, -4, -6,…), this series converges to 0. These are called the trivial zeros of the function and are located at every even negative number. Negative even integers are not the only inputs that result in a 0; these other values that result in 0 are called non-trivial zeros. The Riemann hypothesis concerns the location of all these other non-trivial zeros. It states:
RH: “Every non-trivial zero of the Riemann zeta function has a real part that is ½”
In other words, the Riemann hypothesis posits that all inputs (aside from negative even integers) that when plugged into the Riemann zeta function return a zero, will be in the form of a complex number a+bi where a = ½.
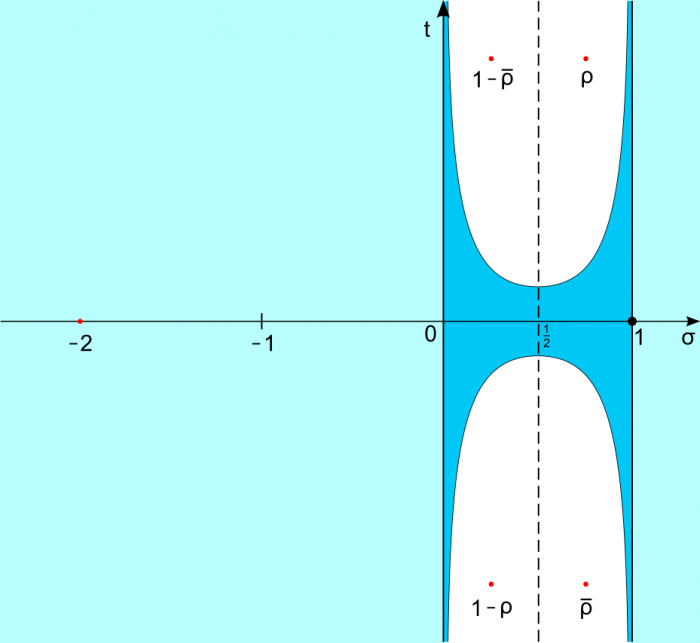
The Riemann hypothesis posits that all non-trivial zeros of the Riemann zeta function fall along the dotted line. Credit: LoStrangolatore via WikiCommons CC-BY SA 3.0
The Riemann hypothesis was first articulated by the German mathematician Bernhard Riemann in 1859. Riemann’s initial motivation in studying the zeta function was related to his work on the distribution of prime numbers along the number line. The Riemann hypothesis is a very important open question in mathematics because many other deep mathematical results rest on it being true. For example, it is strongly believed that the truth of the Goldbach conjecture (see #1) relies on the Reimann hypothesis being true. Several weaker versions of the Goldbach conjecture have been proven on the assumption that the Reimann hypothesis is true. So, solving the Riemann hypothesis has many serious implications in other areas of mathematics.
The Riemann hypothesis is one of the Millenium Prize Problems, a list of unsolved math problems compiled by the Clay Institute. The Clay Institute has offered a $1 million prize to anyone who can prove the Riemann hypothesis true or false.








