Zero is a number that falls squarely between the positive and negative numbers on the number line. Zero is considered an integer, along with the positive natural numbers (1, 2, 3, 4…) and the negative numbers, (…-4,-3,-2,-1).
Zero is a special number in the integers as it is the only integer that is neither positive nor negative. It is also the only integer that is neither a prime nor composite number. It is considered an even number because it is divisible by 2 with no remainder. Zero is the additive identity element in various systems of algebra, and the digit “0” is used as a placeholder value in positional notation systems for representing numbers.
Zero has many interesting properties that make it of interest to mathematicians. If you add or subtract zero from any number, the number remains the same If you multiply 0 by any number, the result is 0. Any number raised to the zeroth (0th) power is 1, so 20=1 and 560=1. In traditional algebra, division by 0 is undefined, so no number can be divided by 0. The number 0 is also an element of the real numbers and complex numbers.
History Of The Number 0
Where did the idea of zero come from? Nowadays, it seems intuitive to us; zero is number that stands for a null quantity—a nothing. We see zeroes everywhere in society, and we naturally understand what they mean and how they can be mathematically manipulated. Historically though, the concept of 0 took quite some time to be universally recognized as an object of mathematics, and many through history argued that the number zero does not exist, or that the idea zero is an incoherent concept.
Many ancient societies did not have an explicit concept of the quantity of zero or a specific digit to use for its representation. Ancient Egyptians and the Babylonians both had some idea of a null quantity and a need for placeholders values in the representation of numbers, but they never developed a distinct digit or concept to represent that quantity or placeholder value. Ancient Egyptian numbering systems were entirely pictorial and did not have positional values, while ancient Babylonians used spaces between numbers to represent positional values.
The Mayans did have an explicit concept of 0 and had a distinct digit to represent the concept and use as a placeholder value in their vigesimal (base-20) calendar system. While Mayan, Olmec, and other pre-Colombian societies were among the first in history to have an explicit and sophisticated understanding of the number 0, these systems did not go on to influence Old World societies in Europe.
The Ancient Greeks, on the other hand, had a complicated relationship with zero. They did not have a symbol for its concept or for it as a placeholder value because they were unsure whether the number 0 could be considered a genuine existing thing. How, they asked, could something (a number) be nothing (zero)? For the Greeks, the natural numbers (1, 2, 3, 4,…) were derived from our understanding of discrete individual objects in the world. Aristotle himself famously argued that 0 does not exist, on the grounds that 0 represents a void or nothingness, and a genuine void or nothingness cannot exist.
The Chinese had an understanding of “0” as a placeholder digit for their counting systems, but they did not consider the digit “0” to represent any distinct number, only a useful symbol. The common understanding of 0 as a distinct number and as a digit for positional notation systems came from India during the 6th century AD. Indian mathematicians at the time developed the first kinds of decimal (base-10) notation systems that incorporated 0 as a distinct digit and had an understanding of zero’s unique mathematical properties. By the 11th century AD, the idea of zero had spread to Western Europe via the influence of Islamic mathematicians living in Spain under the Umayyad caliphate, and the modern-day Arabic numeral system of decimal notation was created. The first use of the English word “zero” dates back to 1589.
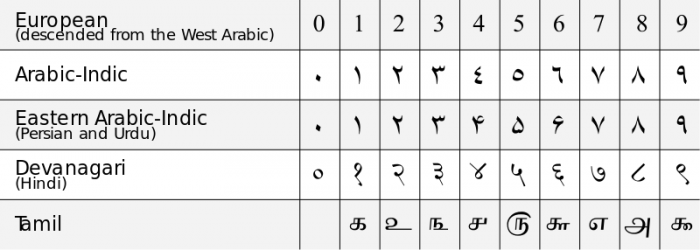
The development of our modern day numeral system from its Indo-European roots. Credit: Madden/WikiCommons, licensed under CC-BY-SA 3.0
Mathematical Properties of Zero
The number zero plays an integral role in almost every field of mathematics. Zero is the smallest non-negative integer and has no natural number proceeding it. Since 0 is an integer, it is also a rational number, a real number, and a complex number. In mathematics, 0 is considered a quantity that corresponds to null amount. One could say that zero is the “quantity” possessed by a set that has no members.
In Algebra
In elementary algebra, zero is often expressed as lying at the center of the number line. The number 0 is considered an even number as it is an integer multiple of the number 2 (2×0=0). 0 is not a prime number because it has an infinite amount of factors, and it is not a composite number because no product of two prime numbers equals the number 0.
With respect to the 4 main arithmetic operators (+, −, ×, ÷) and the exponent operation, the number 0 behaves according to the following rules:
- Addition: x+0=0+x=x. Zero is considered the additive identity element as any number plus or minus zero equals that number
- Subtraction: x-0=x and 0-x=-x
- Multiplication: x⋅0=0⋅x=0. Any number times 0 is also equal to 0.
- Division: 0/x=0, except when x=0. x/0 is a mathematically undefined quantity, as 0 has no multiplicative inverse (no number times 0 gives you 1).
- Exponents: x0=1, except when x=0. There has long been debate over whether 00 is undefined or a well-formed expression. For all positive x, 0x=0.
In expressions involving limits, the quantity 0/0 can pop up in the context of demonstrating limits of rational functions like f(x)/g(x). In these cases, 0/0 is not undefined but represents an indeterminate form. This does not mean the limit is undefined but that it has to be computed via another method, such as finding derivatives. There do exist some algebraic models where division by zero gives a defined quantity, such as the projectively extended real line or the Riemann sphere.
In Set Theory
In set theory, the number 0 corresponds to the cardinality the “empty set” or the “null set” (commonly represented as {} or {∅}. The cardinality of a set is the amount of elements in that set if one does not have any oranges, then one has a set of 0 oranges (an empty set of oranges).
Zero is often used as the starting point in set theory to construct the rest of the natural numbers. These von Neumman constructions, named after the renowned polymath John von Neumann constructs the natural numbers by defining 0={} and defines a successor function S(a) = a ∪ {a}. The entirety of the natural numbers can be constructed from the recursive applications of the successor function beginning with the empty set:
0 = {}
1 = 0 ∪ {0} = {0} = {{}}
2 = 1 ∪ {1} = {0,1} = {{}, {{}}}
3 = 2 ∪ {2} = {0, 1, 2} = {{}, {{}}, {{}, {{}}}}
and so on. Following this pattern, one can construct the entire infinite set of the natural numbers. In this way, we can say that each natural number is corresponded to the set containing all the natural numbers before it.
In Physics
In the context of making quantitative measurements in physics, 0 is considered to be the baseline from which all other measurements of units are made. Very often, the baseline of 0 corresponds to some physically significant variable that is naturally distinguishable from all other magnitudes of measurement.
For instance, in the Kelvin scale, a temperature of 0 K correspond to absolute 0— the coldest temperature that is physically possible. In the Celsius temperature scale, 0 °C is defined as the freezing point of water at atmospheric pressures. In the context of dynamics and electromagnetism, a value of 0 is given to the position in which a system has the minimal possible amount of potential energy. For example, the ground state of an atom, the lowest possible energy level for the electrons in the atom, is often assigned a value of 0.
Likewise, in the context of kinematics, the reference frame from which observations of motion are made is defined as having a center point laying on the origin of the coordinate axis at point (0, 0). In the case of conserved quantities, like mass-energy, momentum, and angular momentum, the total amount of change to conserved quantities in an isolated system is always equal to 0.
In Computer Science
Computers store information in the form of bits—long sequences of 1s and 0s. In this binary representation, 0 correspond to an “off” position and is contrasted with the “on” position designated by 1. A value of 0 on an electrical circuit means that the circuit is off and does not have any electrical flow. Similarly, many computational logics define “0” to be the character that represents a false truth value.
In computer databases, the elements of an array are counted using a zero-based counting system. This means that for a set with n elements, the elements have indices starting with 0. Thus, an element with an index number of 0 is actually the first element in the series, and an index number of 1 corresponds to the second element, and so on. In general, the nth term of a set has an index number corresponding to n-1. This counting system can cause confusion to new programmers who are used to intuitively assigning index values beginning with 1.








