How To Find Vertical Asymptotes

In mathematics, an asymptote of a function is a line that a function get infinitesimally closer to, but never reaches. In more precise mathematical terms, the asymptote of a curve can be defined as the line such that the distance between the line and the curve approaches 0, as one or both of the x and y coordinates of the curve tends towards infinity. In other words, an asymptote is a line on a graph that a function will forever get closer and closer to, but never actually reach.

There are three major kinds of asymptotes; vertical, horizontal, and oblique; each defined based on their orientation with respect to the coordinate plane. Vertical asymptotes are the most common and easiest asymptote to determine. A vertical asymptote is equivalent to a line that has an undefined slope. In short, the vertical asymptote of a rational function is located at the x value that sets the denominator of that rational function to 0. A rational function is a function that is expressed as the quotient of two polynomial equations. For example, a graph of the rational function ƒ(x) = 1/x² looks like:

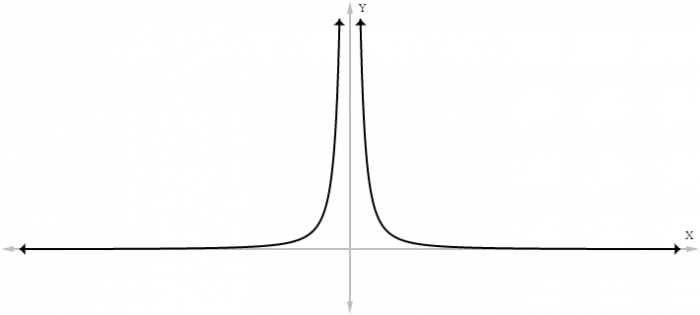
All graphs generated with <http://www.graphfree.com/>

Setting x equal to 0 sets the denominator in the rational function ƒ(x) = 1/x² to 0. Hence, this function has a vertical asymptote located at the line x=0. Vertical asymptotes are unique in that a single graph can have multiple vertical asymptotes. Conversely, a graph can only have at most one horizontal, or one oblique asymptote.

The Concept Of An Asymptote

Initially, the concept of an asymptote seems to go against our everyday experience. Physical representations of a curve on a graph, like lines on a piece of paper or pixels on a computer screen, have a finite width. By extending these lines far enough, the curve would seem to meet the asymptotic line eventually, or at least as far as our vision can tell. One must keep in mind that a graph is a physical representation of idealized mathematical entities. An idealized geometric line has 0 width, so a mathematical line can forever get closer and closer to something without ever actually coinciding with it.

In some ways, the concept of “a value that some quantity approaches but never reaches” can be considered as finding its origins in Ancient Greek paradoxes concerning change, motion, and continuity. Here is a famous example, given by Zeno of Elea: the great athlete Achilles is running a 100-meter dash. In order to run 100 meters he must first cover half the distance, so he runs 50 meters. In order to run the remaining 50 meters, he must first cover half of that distance, so 25 meters. In order to cover the remaining 25 meters, he must first cover half of that distance, so 12.5 metes. In order to cross the remaining 12.5 meters, he must first cross half of that distance, so 6.25 meters, and so on and so on.

Extrapolating this reasoning ad infinitum leads us to the counter-intuitive conclusion that Achilles will never cross the finish line. There will always be some finite distance he has to cross first, so he will never actually reach the finish line. Philosophers and mathematicians have puzzled over Zeno’s paradoxes for centuries. Unbeknownst to Zeno, his paradoxes of motion come extremely close to capturing the modern day concept of a mathematical asymptote.

Definition Of An Vertical Asymptote

The first formal definitions of an asymptote arose in tandem with the concept of the limit in calculus. The limit of a function is the value that a function approaches as one of its parameters tends to infinity. So a function has an asymptote as some value such that the limit for the equation at that value is infinity.

We will only consider vertical asymptotes for now, as those are the most common and easiest to determine. Here are the general conditions to determine if a function has a vertical asymptote: a function ƒ(x) has a vertical asymptote if and only if there is some x=a such that the output of the function increase without bound as x approaches a. That is, a function has a vertical asymptote if and only if there is some x=a such that the limit of the function at a is equal to infinity.

That last paragraph was a mouthful, so let’s look at a simple example to flesh this idea out. The following is a graph of the function ƒ(x) = 1/x: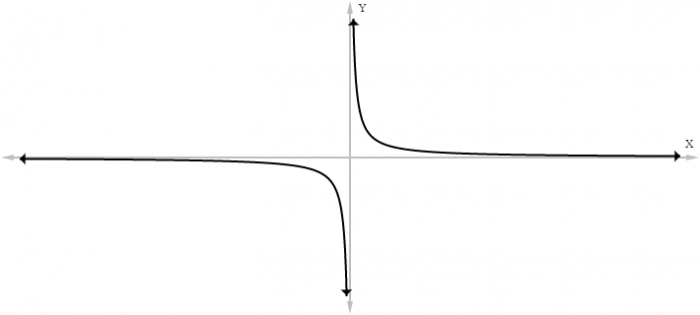

This function takes the form of an inverse curve. Notice the behavior of the function as the value of x approaches 0 from both sides. As the x value gets closer and closer to 0, the function rapidly begins to grow without bound in both the positive and negative directions. Lets’s see what happens when we begin plugging x values that get close and closer to 0 into the function:

ƒ(1) = 1/1 = 1

ƒ(0.5) = 1/0.5 = 2

ƒ(0.25) = 1/0.25 = 4

ƒ(0.1) = 1/0.1 = 10

ƒ(0.01) = 1/0.01 = 100

ƒ(0.001) = 1/0.001 = 1000

ƒ(0.000001) = 1/0.000001 = 1,000,000

ƒ(0.00000001) = 1/0.00000001 = 100,000,000

Notice that as x approaches 0, the output of the function becomes arbitrarily large in the positive direction towards infinity. Most importantly, the function will never cross the line at x=0 because the function is undefined for the ƒ(0) (1/0 is not defined in normal arithmetic). Similarly, if one approaches 0 from the left, the values are

ƒ(-0.5) = 1/-0.5 = -2

ƒ(-0.25) = 1/-0.25 = -4

ƒ(-0.1) = 1/-0.1 = -10

ƒ(-0.01) = 1/-0.01 = -100

ƒ(-0.001) = 1/-0.001 = -1000

ƒ(-0.000001) = 1/-0.000001 = -1,000,000

ƒ(-0.00000001) = 1/-0.00000001 = -100,000,000

As x approaches 0 from the left, the output of the function grows arbitrarily large in the negative direction towards negative infinity. This is a double-sided asymptote, as the function grow arbitrarily large in either direction when approaching the asymptote from either side. Some functions only approach an asymptote from one side.

How To Find A Vertical Asymptote

Finding a vertical asymptote of a rational function is relatively simple. All you have to do is find an x value that sets the denominator of the rational function equal to 0. Here is a simple example:

What is a vertical asymptote of the function ƒ(x) = (x+4)/3(x-3) ?

This one is simple. All we have to do is find some x value that would make the denominator tern 3(x-3) equal to 0. A moment’s observation tells us that the answer is x=3; the function ƒ(x) = (x+4)/3(x-3) has a vertical asymptote at x=3.

Instead of direct computation, sometimes graphing a rational function can be a helpful way of determining if that function has any asymptotes. A graph for the function ƒ(x) = (x+4)/(x-3) looks like: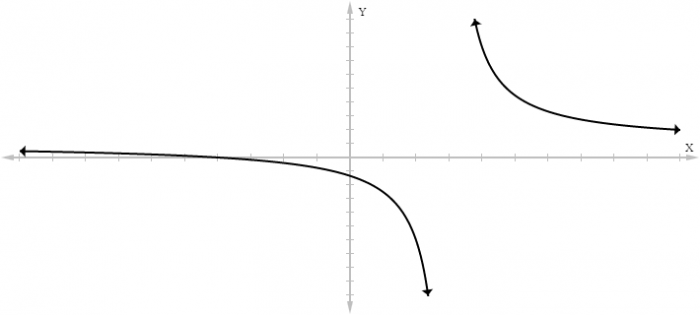

Notice how as x approaches 3 from the left and right, the function grows without bound towards negative infinity and positive infinity, respectively. Simply looking at a graph is not proof that a function has a vertical asymptote, but it can be a useful place to start when looking for one.

More Problems With Solutions

Let’s look at some more problems to get used to finding vertical asymptotes.

(1)

What is the vertical asymptote of the function ƒ(x) = (x+2)/(x²+2x−8) ?

Solution:

Once again, we need to find an x value that sets the denominator term equal to 0. In this case, the denominator term is (x²+2x−8). We can find out the x value that sets this term to 0 by factoring. Factoring (x²+2x−8) gives us:

(x²+2x−8) = (x+4)(x-2)

This function actually has 2 x values that set the denominator term equal to 0, x=-4 and x=2. Thus, the function ƒ(x) = (x+2)/(x²+2x−8) has 2 asymptotes, at -4 and 2. Graphing this equation gives us: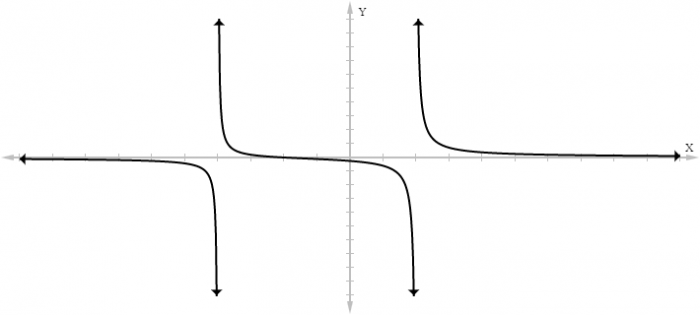

By graphing the equation, we can see that the function has 2 vertical asymptotes, located at the x values -4 and 2.

(2)

What is the asymptote of the function ƒ(x) = (x³−8)/(x²+9) ?

Solution:

To figure out this one, we need to set the denominator equal to 0, so:

x²+9 = 0

x² = -9

Whoops! This equation has no solution.  Any number squared is always greater than 0, so, there is no value of x such that x² is equal to -9. Thus, there is no x value that can set the denominator equal to 0, so the function ƒ(x) = (x+2)/(x²+2x−8) does not have any vertical asymptotes!

(3)

What is(are) the asymptote(s) of the function ƒ(x) = x/(x²+5x+6) ?

Solution:

Once again, we can solve this one by factoring the denominator term to find the x values that set the term equal to 0. Factoring the bottom term x²+5x+6 gives us:

x²+5x+6 = (x+2)(x+3)

This polynomial has two values that will set it equal to 0, x=-2 and x=-3. Thus, the function ƒ(x) = x/(x²+5x+6) has two vertical asymptotes at x=-2 and x=-3. Graphing this function gives us: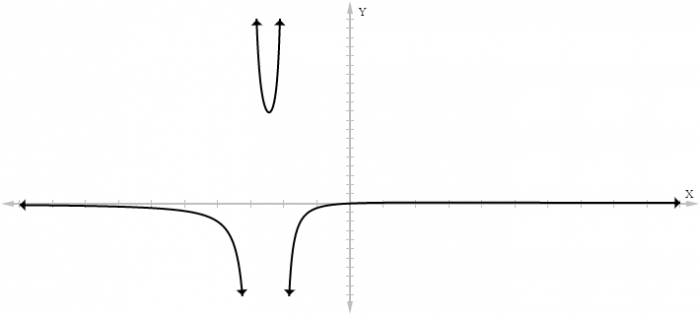

As this graph approaches -3 from the left and -2 from the right, the function approaches negative infinity. As it approaches -3 from the right and -2 from the left, the function grows without bound towards infinity. The placement of these two asymptotes cuts the graph into three distinct parts.

In summation, a vertical asymptote is a vertical line that some function approaches as one of the function’s parameters tends towards infinity. A function will get forever closer and closer to an asymptote bu never actually touch. A function has a vertical asymptote if and only if there is some x=a such that the limit of a function as it approaches a is positive or negative infinity. One can determine the vertical asymptotes of rational function by finding the x values that set the denominator term equal to 0.