Graph Quadrants: Definition And Names

Quadrants are how two-dimensional Cartesian systems are divided and the value of the points graphed within them depends on their location relative to the X-axis and the Y-axis. The quadrants divide the plane into four separate regions, and each of these regions is bounded by half of an axis.

They are usually given Roman numerals to identify them, and moving counterclockwise from the top-right to the bottom-right they are: I, II, III, and IV.

Defining Quadrants On A Cartesian Graph/Plane

The quadrants are based on a plane divided by two axes. The X-axis is the horizontal axis, while the Y-axis is the vertical axis. The Intersection of the two axes is where both X and Y values are at zero. Positive Y values are found above the horizontal line while negative values are found below it. Similarly, positive X values are found to the right of the Y-axis and negative X values found to the left of the Y axis.

Thus, quadrant I contains points where both values are positive (+, +) and quadrant II contains values where the X is negative but the Y is positive (-, +). Quadrant III contains points where both values are negative (-, -) and quadrant IV contains points where the X is positive but the Y is negative (+, -).

In trigonometry, there are three different functions that can be plotted on a Cartesian plane. They are sine, cosine and tangent. A sine graph is a graph which starts at 0 and moves up to 1 by π/2 radians (90°) , and then moves down to -1. It has a symmetrical up-down curve. Cosines are plots which start at 1, not 0 and moves up by π radians (180°) until it moves downwards again towards -1. It looks similar to a plot of Sine, except for the origin. Meanwhile, a tangent function has a shape quite unlike the other two functions. The tangent function runs between negative and positive infinity, but it crosses through the origin of 0 and it also crosses at every π radians (180°). This gives it a pattern of repeating shallow curves.

In quadrant I, every plot of Sine, Cosine and Tangent will be positive. In quadrant II, only Sine, Cosec (sine) graphs will be positive. In quadrant III, only tan and cot (tangent) plots will be positive, and in quadrant IV only cos and sec (cosine) plots will be positive. The mnemonic for this is “All Science Teachers (are) Crazy”.

The Cartesian plane/coordinate system gets its name from the French philosopher and mathematician Rene Descartes, who came up with the idea and published it in 1637. The idea had been independently created by Pierre de Fermat, though Fermat didn’t publish his work like Descartes did. While both Descartes and Fermat used a single axis in their version of the coordinate system, later mathematicians would expand on their work and standardize the system with two axes.

Transformations

An example of a reflection over an axis. This first reflection is followed by a second reflection over an axis that isn’t parallel to the first axis. Photo: By Simx2=rotOK.png: Toobazderivative work: McSush (talk) – File:Simx2=rotOK.png, CC BY 2.5, https://commons.wikimedia.org/w/index.php?curid=8385414

Euclidean transformations, or Euclidean motions, are movement/mapping of points within a Euclidean plane to other points that preserve the distances between said points. There are four different types of transformations: rotations, translations, reflections and glide reflections.

A Euclidean rotation means that the distance from the center to any point will stay the same, the points rotate around the chosen center of the shape. A reflection means that the shape or geometric object is flipped over one of the plane’s axes. This means that a chosen point will cross an axis into another quadrant. For example, if a point is listed as 4, -3, a reflection of this point would make it -4, 3. A glide reflection is a specific type of reflection where the shape is first reflected then translated, or translated then reflected. A translation of a geometric shape just means that the shape moves a given direction with a given magnitude of change. The key point about a translation is that every point in the shape must move the same direction with the same distance.

Cartesian Systems In Two Dimensions

Choosing an x-axis will determine the direction of the y-axis. The y-axis will be perpendicular to the x-axis and move through the point marked 0 on the x-axis. Yet a choice can be made over which half of the line’s two halves will be labeled positive or negative. This choice is what gives a Cartesian plane its orientation or handedness. That said, while it is up to the creator of the graph to choose which direction is positive or negative, the normal way of labeling the positive/negative regions is to have the positive X-axis run to the right while the positive Y-axis runs up.

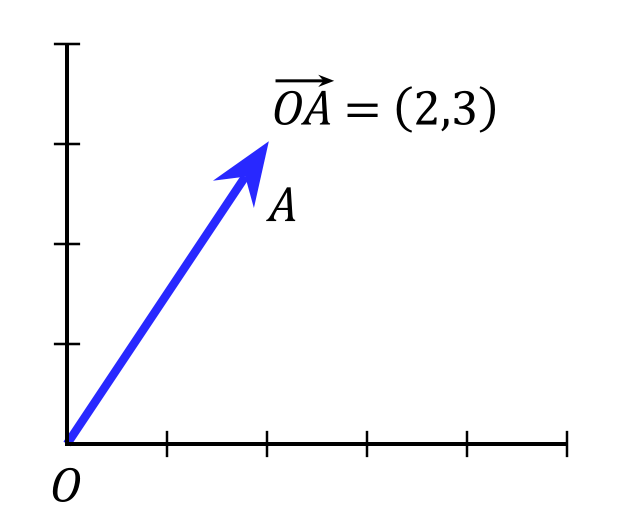
A Note On Vectors

Photo: Acdx via Wikimedia Commons, CC 3.0

Points in a Cartesian coordinate system may also be defined as vectors or an arrow that points from the origin of the coordinate plane (0, 0) to the point. Vectors have two qualities: direction and magnitude. The direction is just the direction (up, down, left, right) that the vector is moving and magnitude represents the amount of movement in that direction. If the coordinates stand-in for spatial positions, then the vector that begins at the origin and moves to the point is usually represented with “r”. The vector that exists from origin to point is usually represented as r = xi, + yj. “I” and “j” are (1/0) and (0/1) respectively, representing the direction of the vector in terms of the X and Y axis.

Graphing On A Cartesian Plane

Photo: By DanielPenfield – Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=9402369

A Cartesian graph is a graph that can be displayed on Cartesian plane. They show points on a Cartesian graph that can be expressed in terms of their linear relationship with one another.

The line plot is the most basic type of plot/graph created on a Cartesian plane. It is used to visualize how two variables are related to each other, like how a quantity changes with time. A line plot has a series of points that provide relevant information about how one variable changes with regard to another variable. Line segments are then used to connect the points and show a trend.

Another common type of graph is a scatter plot, which shows individual instances/occurrences of two different variables for a given set of data. They are used to determine relationships between two quantitative variables, if any relationship exists.