The derivative of a function is a function that tells you the rate of change of the initial function at any particular point on that function. One can think of a derivative of a function as a measure of how sensitive the output of the initial function is to small changes in its input. A derivative tells us how quickly a function is changing at any given point in time. As such, derivatives are useful for modeling situations involving rates of change, such as displacement, velocity, and acceleration.
The derivative of the function:
![]()
can be determined by a special rule for finding the derivative of functions in the form of ex. The general rule is:
![]()
So using this rule, we can determine that:
![]()
That is, the derivative of the function ƒ(x) = e2x is ƒ'(x) = 2e2x. This derivative tells us the rate of change the output of the original function per change in input. Basically, the two equations tell us that the output of the function ƒ(x) = e2x grows by a factor of 2e2x per input. So if our x value is one, plugging that value into the equation gives us:
![]()
![]()
These equations tell us two things. First, at the point x=1, the function ƒ(x) has an output of e2. Second, the derivative tells us that at the point x=1, the output of ƒ(x) is changing by a factor of 2e2.
What Is A Derivative?
As stated previously, the derivative of a function is a measure of how sensitive the output of a function is to changes in its input. The derivative of ƒ(x) measures the rate of change of the output of ƒ(x) with respect to changes in x.
Imagine the simple case where we have some linear equation y=2x+3. Further, lets pick two sets of x y coordinates that fall on this line: (1,5) and (2,7). What is the rate of change of the function with respect to x between these two points? We can figure this out by computing:
![]()
This means that between those two points, the output of the function is changing by a factor of 2. Notice that this value of 2 is also equal to the slope of the linear equation y=2x+3.
In fact, for any two points on the equation y=2x+3, the rate of change will always be 2. This means that at every point of our function, the output of the function is growing by a factor of 2 with respect to x. Incidentally, this gives us our first rule for finding derivatives: In the case that ƒ(x) is some linear function y=mx+b:
![]()
That is, for any linear function in the form y=mx+b, the derivative of that function is equal to the slope m. If we think about linear equations expressing some rate of change of y with respect to changes in x, the slope of the function m gives us that rate of change, as for each input, the rate of change of the output changes by a factor of 2.
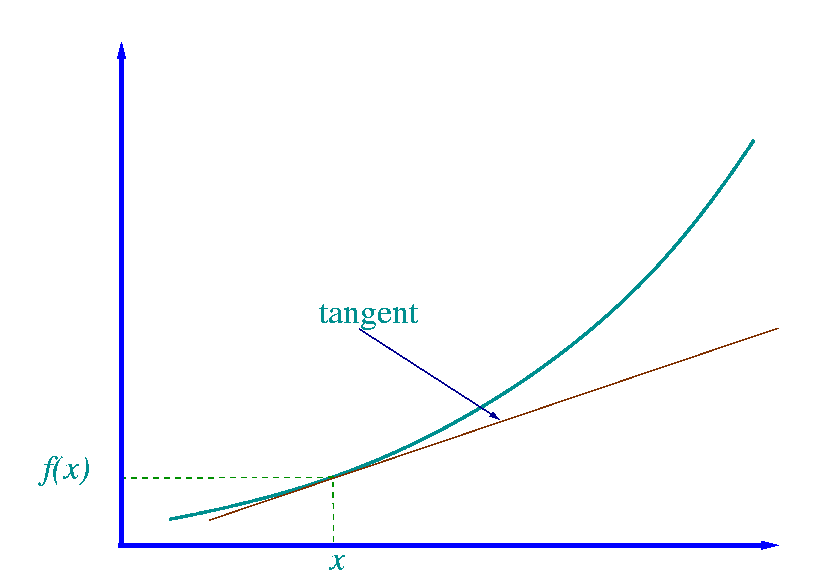
The process of finding a derivative for a higher degree function (e.g. x2, x3) generalizes this process of finding the slope between two point and finds the limiting value the ratio Δy/Δx approaches as Δx becomes arbitrarily small. The result is that the derivative of a function at some point essentially tells us the slope of the graph at a single point. This is also seen in the fact that the derivative of a function at some point gives the slope of a line that is tangent to the graph at that point.
OK, that is all well and good, but how do we go about finding the rate of change of a function like ƒ(x)=x2 at each point in time? Unlike an equation like y=mx+b, the rate of change of the function ƒ(x)=x2 is not constant and is changing at every point. How do we capture the rate of change of this kind of power function?
Remember in the case of the linear equation, we found the rate of change of the equation by finding the ratio of change in x over change in y (Δy/Δx). Let’s start with the function ƒ(x)=x2. Picking two values for x, we get ƒ(1)=1 and ƒ(2) = 4. Solving for Δy/Δx gives us (4-1)/(2-1)=4. The slope of the line passing between these two points is 4. Now, imagine we repeated this process, we choose x values really close to each other, say 1 and 1.5. This gives us:
![]()
What if we go even closer? How about 1 and 1.1? Plugging these values in gives us:
![]()
What about 1 and 1.01?: These give us:
![]()
Notice that as our Δx grows arbitrarily small, the ratio of Δy/Δx approaches some value, in this case, 2. In graphical terms, this means that if we keep choosing smaller and smaller differences of x, we closer and closer approximate the slope of the function at a single point. This will eventually give us the derivative of the function at that point, which is 2.
So we have just figured out a way to approximate a derivative of a function at a single point. The derivative of a function can be approximated by series of smaller and smaller Δx that approach a point. This gives us a general definition for giving the derivative of a value written in limit notation; that is:
![]()
Essentially, this equation says that the derivative of ƒ(a) is equal to the limit that the ratio Δy/Δx approaches as h gets infinitesimally small. A value of h that is very close to 0 will give you a good approximation of the slope of the graph at that point. The idea is that as we choose smaller and smaller values for h, we get closer and closer to the slope of the tangent line at that point on the function. This is the formal definition of a derivative and can be used to derive a derivative function—i.e. a function that maps all input values to the rate of change of the initial function at some time.
Let’s go back to our function ƒ(x)=x2. If we plug this function into our derivative definition, we should be able to derive a derivative function for ƒ(x)=x2. Doing so gives us:
![]()
![]()
![]()
Factoring out the h gives us:
![]()
Since in this equation, h is supposed to be some really, really, tiny value, we can essentially ignore any h in the equation and simplify it as:
![]()
That is, the derivative function of ƒ(x) = x2 is just ƒ'(x) = 2x. The rate of change of the function x2 at any point x, is equal to 2x. So at x=1, ƒ'(1)=2, at x=2, ƒ'(2)=4, at x=3, ƒ'(3)=6, and so on. The derivative function gives the rate of change of the initial function at each point with respect to changes in the input value. For every x value in this graph, the function is changing at a rate that is proportional to 2x.
General Rules For Computing Derivatives
The first rule involves the derivative of a constant function. For any function that gives a constant output, the derivative of that function is 0. This is:
![]()
Since a constant function only gives the same output, it never changes so its rate of change is always 0. So if ƒ(x)=7 then ƒ'(x)=0.
Next, generalizing the previous process of deriving the derivative of x2 to any nth degree polynomial gives us a general rule for finding the derivative of polynomial terms:
![]()
This is called the power rule and can be used to compute the derivatives of multi degree polynomials. Using the power rule, we can determine that the derivative of x3 is 3x2, the derivative of x4 is 4x3 and so on.
For exponential functions, one can find the derivative by multiplying the function itself by the natural log of the base. This is:
![]()
This is called the exponent rule. The exponent rule is a more generalized version of the special rule for finding the derivative of ex. Of all functions, f(x)=ex is the only function whose derivative is itself. That is, the slope of all line tangent to the graph ex is just ex.
![]()
The four above expressions are the most common rules for finding the derivatives of expressions. Additionally, there are rules that govern the combination of functions and their derivatives. For example, there is the sum rule which is:
![]()
The sum rule tells us that if some function h is the sum of two other functions f and g, then the derivative of h is equal to the sum of the derivatives of f and g. The sum rule allows us to find the derivative of each term in a polynomial equation, and add them together to get the total derivative. For instance imagine ƒ(x)= x3+4x2-3x. The sum rule tells us that the derivative of this function will be equal to the sum of the derivatives of its constituent functions, so ƒ'(x)=3x2+8x-3
Next is the product rule, which give a formula for finding the derivatives of the product of functions. The product rule is:
![]()
The product rule tells us that the derivative of the product of two functions is equal to the first function times the derivative of the second, plus the second function times the derivative of the first. So the derivative of ƒ(x)=sin(x)x2 would be ƒ'(x)=sin(x)2x + x2cos(x). You can remember this order of the product rule with the mnemonic “left dee right, right dee left” (LDR RDL)
Lastly is the chain rule, which describes the derivative of a composition of functions. If some function is the composition of two others, then the chain rule tells us that the derivative of the composite function is equal to the derivative of the first function when evaluated at g(x), multiplied by the derivative of g(x). Symbolically this is:
![]()
The chain rule allows us to put a function within a function and gives the derivative of that composite function.
Using these rules, one can compute the derivatives of most standard polynomial equations. Some functions are more complex, but a solid application of the above rules should allow you to peel apart the layers of any real-valued function to derive its derivative.









