A quadratic equation is any equation in the form of ax2+bx2 +c. Quadratic equations are most commonly found in the context of quadratic function
s—functions such as ƒ(x) = x2 + x + 1 or ƒ(x) = 6x2−4x + 9. In more precise mathematical terms, a quadratic is any polynomial expression that has a degree of 2.
In the above quadratic equation, the three coefficients a, b, c are called:
- a is the leading term
- b is the linear term
- c is the constant
The graph of a quadratic function is called a parabola.

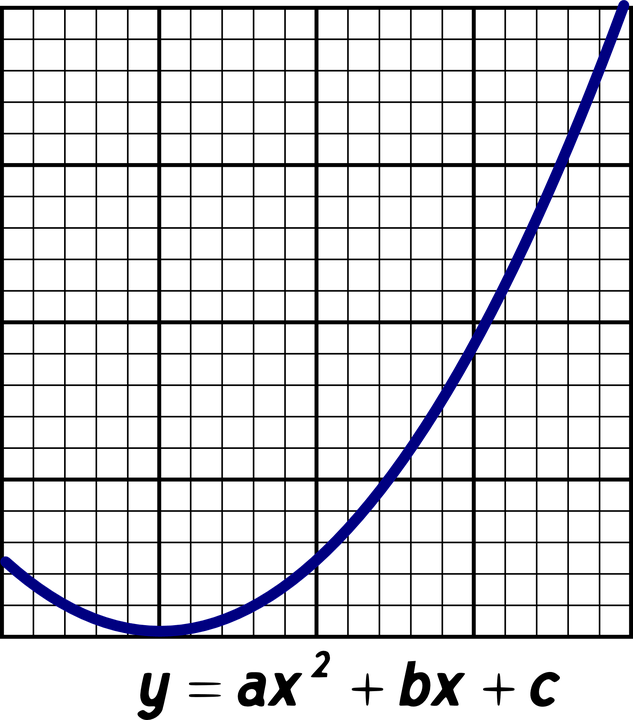
Credit: graphfree
For example, the above graph is the graph of the simple quadratic function ƒ(x) = x2.
The exact shape and orientation of the graph are determined by the values of the coefficients of the quadratic function a, b, and c.
When |a| > 1, such as 3 or 4, the graph gets “skinnier.” This is because the graph is growing at 3 times or 4 times the rate. Conversely, if |a|<1 such as 0.5 or 0.25, then the graph gets “fatter” because it is growing at half or one-fourth the rate.
The value of a also determines which way the parabola is facing. If a is positive, then the parabola faces up and opens at the top. If a is negative, then the parabola faces down and opens downward.
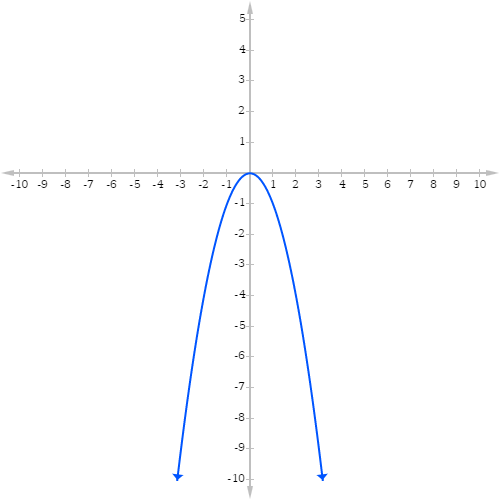
Credit: graphfree
The above picture is a graph of the function ƒ(x) = –x2. Because the leading term is negative (a=-1) the graph faces down. One way to remember this relationship between a and the shape of the graph is If a is positive, then the graph is also positive and makes a smiley (“positive”) face. If a is negative, then the graph makes a frowny (“negative”) face.
The b term (linear term) determines, roughly, the amount of horizontal offset of the graph. Changing the linear term moves the graph over left and right. It also slightly changes the vertical offset of the graph, though not as much as the c term. Changing the constant term determines the amount of vertical offset of the graph. When c is positive, the graph is shifted up, when c is negative, the graph is shifted down.
Here is a nice link to a GeoGebra tool that lets you play around with the different coefficient values and see how changing them around changes the appearance of the graph. Take some time messing around with this app to get an intuitive feel for how quadratic functions operate. Notice that when a = 0, the graph takes on the form of a straight line. When a = 0, the quadratic can be written as a linear equation.
Parabolas are interesting because they pop up all over nature and have a lot of engineering applications. For example, Galileo discovered in the 17th century that the motion of a projectile through the air always takes the shape of a parabola and parabola-shaped curves pop in models relating to electromagnetism, population growth, and engineering.
Vertex Of Quadratics
Notice that every parabola has a point where it changes direction. This is called the vertex of the parabola and is the minimum point on a positive parabola and the maximum point on a negative parabola. The vertex is the inflection point of the graph where it starts to change direction from the negative direction to the positive or vice versa.

The different parts of a parabola. The vertex is located at the inflection point where the graph changes direction. Credit: Melikamp via WikiCommons CC-BY SA 3,0
How do you figure out where the vertex is? More specifically, how do you find the x- and y- coordinate for the vertex of any given parabola? We will look at two different methods, one involving a different form of quadratic equations and another that uses a bit of calculus to compute the vertex.
How To Find The Vertex Of A Parabola
Method 1. Use Vertex Form
One way to understand the vertex is to see the quadratic function expressed in vertex form. The vertex form of a quadratic function can be expressed as:
Vertex Form: ƒ(x) = a(x−h)2 + k
Where the point (h, k) is the vertex. This equation makes sense if you think about it. In the case of an upright parabola, the leftmost term will always be positive so the lowest it can possibly be is 0. Therefore, the smallest possible y-value is y=k which happens when the quantity x−h = 0, or in other words, when x = h. The same reasoning holds for downward parabolas. y=k is the highest possible y value, which obtains when h = x.
(Note: the a in the vertex form is the same a in the standard form ax2 + bx2 + c)
So the vertex form of a quadratic equation lets us “read off” the location of the vertex just by looking at the formula. But quadratics are normally not written in vertex form, so we need a way to convert between the standard presentation and vertex form. We can do this by completing the square. We will take a look at the quadratic ƒ(x) = 2x2−4x + 5 as a specific example:
Complete the square
| Standard form | y = 2x2−4x + 5 |
| Isolate the x2 and x terms | y−5 = 2x2−4x |
| Factor out the leading coefficient | y−5 = 2(x2−2x) |
| Create the perfect square trinomial (Note: since we factored out a 2 previously from the right and have a y on the left, whatever we add on the right has to be multiplied by 2 on the left) | y−5+2 = 2(x2−2x+1) |
| Simplify and convert the right side to a difference of squares | y−3 = 2(x−1)2 |
| Isolate the y term | y = 2(x−1)2 + 3 |
| Read off the vertex point | Vertex = (h, k) = (1, 3) |
There is a quick and sneaky way to quickly find the right h and k values without completing the square. When given the standard form of a quadratic (ax2 + bx2 + c) you can find the h and k values as:
h = (-b/2a) and k = ƒ(h)
Just compute the h value and plug it into the function to get the k value.
Converting from vertex form back to standard form is easy. Just multiply out the squared part and simplify the entire expression.
Method 2: Derivatives
Another way of finding the vertex is by using the tools of calculus and derivatives.
Consider the behavior of a quadratic function as it approaches its vertex. For an upward parabola, when coming from the left, the graph initially decreases rapidly. As it approaches the vertex, this rate of decrease gets slower and slower until it reaches the vertex, after which it changes directions and begins to increase. As you go further right, the graph grows quicker and shoots off.
Imagine a line that lies tangent to the parabola. When you start on the left, the tangent line is very steep. As you move to the right, the line becomes less and less steep, until it hits the vertex and becomes a flat line. As you keep moving right, the line gets steep again the further you go.
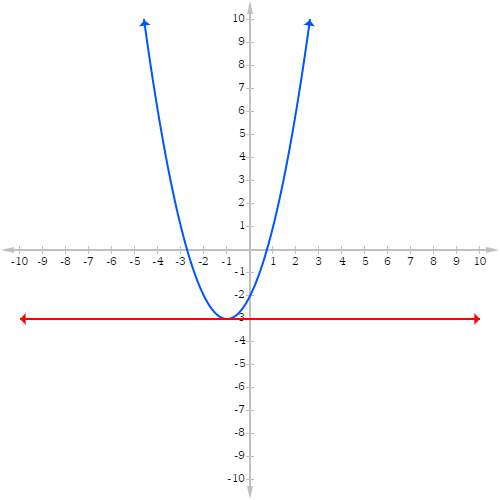
The tangent line of the vertex of a parabola. Credit: graphfree
When the tangent line hits the vertex, it is a flat line. The reason why it is flat is because at the vertex of the parabola the rate of change of the quadratic function is 0. In calculus terms, the vertex of a parabola is located at the point where its derivative is equal to 0. Drawing a line tangent to the vertex will always result in a straight line, which is an indication that the derivative of the function is 0 at that point.
So one way to find the vertex of a parabola is to find the derivate, compute the x value where the derivative is 0, and plug that back into the quadratic to find the y value of the vertex. Let’s see this in action with the function ƒ(x) = x2−2x + 2.
Step 1: Find the derivative of the quadratic
ƒ(x) = x2+2x − 2
ƒ'(x) = 2x+2
Step 2: Solve for x when ƒ'(x) = 0
ƒ'(x) = 2x+2
0 = 2x+2
-1 = x
So -1 is the x-coordinate of the vertex.
Step 3: Plug the result from step 2 into the original quadratic
ƒ(x) = x2+2x−2
ƒ(-1) = (-1)2−2(-1) − 2
ƒ(-1) = -3
So the y-coordinate of the vertex is -3. Together, we get the vertex of the parabola at the point (-1, 3).
In order to tell if the vertex is a minimum or maximum point of the function, take a look at the leading a term of the quadratic:
- If a > 0 then the vertex (h, k) is a minimum
- If a < 0 then the vertex (h, k) is a maximum
To sum up the major points:
- A parabola is the shape of a graph made by a quadratic function ax2 + bx2 + c
- The inflection point where the graph changes direction is called the vertex of the parabola.
- The vertex form of a quadratic is in the form ƒ(x) = a(x−h)2 + k where point (h, k) is the vertex
- The vertex is the minimum of an upward parabola and the negative of a downward parabola
- The vertex of a parabola can be found by two main methods:
- Completing the square
- Differentiation








