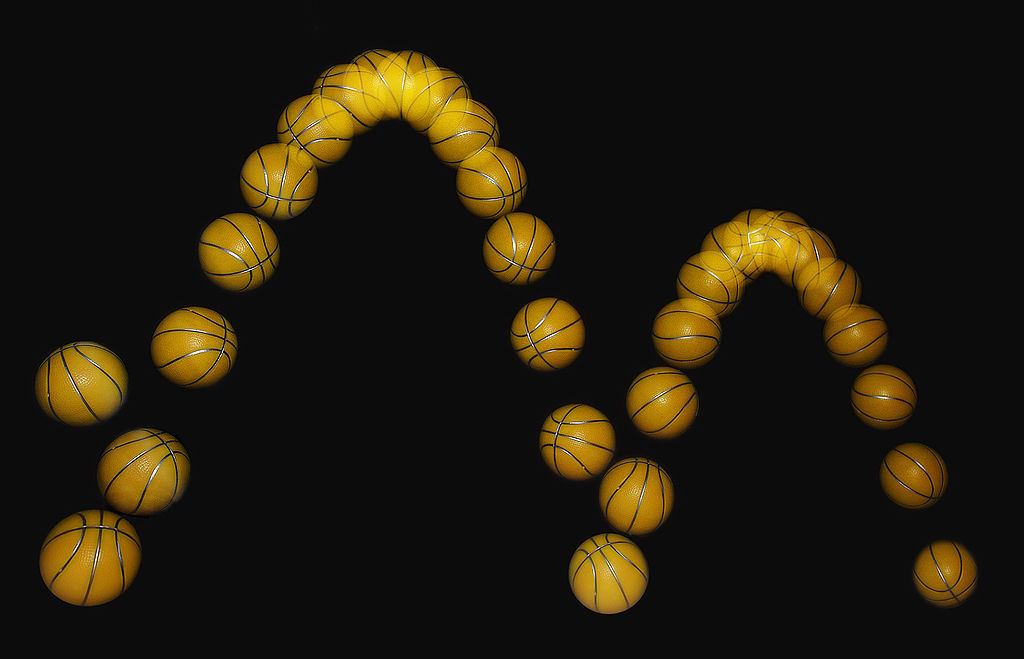
Grab a baseball and toss it straight up. What happens? As you initially throw the baseball, it will gains some height. The ball begins to slow its upward ascent before reaching the highest point of its movement after which it reverses direction and falls back towards the ground. The further the ball falls down, the faster it falls. What happens if you throw the ball at a 45-degree angle up from eye level? You will see the ball trace out an arc in the sky, slowing down before ascending to a highest point in its path, then falling back to the ground.
Why does the ball move the way it does? Why does it climb up an arc to some highest point and then fall back towards the ground? Why does its ascending motion slow down, and its descending motion speed up? In our example, the baseball is a projectile. A projectile is a moving object that is solely under the influence of gravity. Things like cannonballs, bullets, baseballs, and trebuchets are all subject to projectile motion.
TL;DR: Too Long, Didn’t Read
The main equations of motion for a projectile with respect to time t are:
Horizontal velocity = initial horizontal velocity
Vx = Vx0
Vertical velocity = (initial vertical velocity)−(acceleration)(time)
Vy = Vy0−gt
Horizontal distance = (horizontal velocity) (time)
DH = Vx0 t
Vertical distance = (initial vertical velocity)(time)−(½)(acceleration from gravity)(time)2
DV = Vy0t−½gt2
The characteristic motion of projectiles can be explained by two things: inertia and gravity. We will take a look at each of these components.
Inertia
Say you are driving in your car. A cat walks in front of you and you rapidly push the brakes. As the car slows down, your body wants to continue to move and you lurch forward. Why does this happen? The answer is simple: inertia. Inertia is simply the tendency for a body to continue in a state of constant motion. The concept of inertia can be summarized by Newton’s first law of motion which states that an object at rest tends to stay at rest and an object in motion tends to stay in motion. The inertia of an object is just the tendency for some object to “keep doing what it’s doing.” A ball traveling 4m/s to the left will remain traveling 4 m/s to the left, a block that is at rest at 0 m/s will remain at rest at 0 m/s.
As you are driving your car, your body is moving at the same velocity as your car. When you slam on the brakes, the velocity of the car goes to 0, but your body continues in its state of motion. The inertia of your body is why you feel yourself push into the seatbelt.
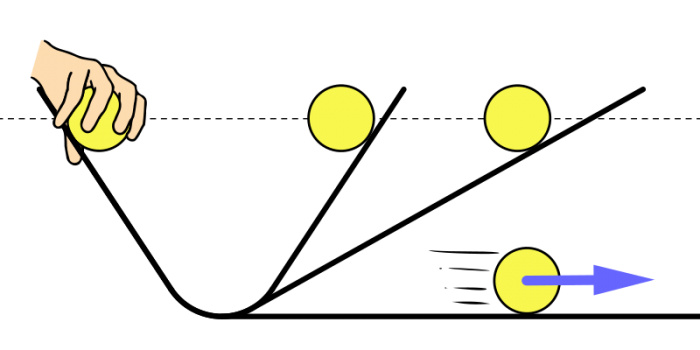
Inertia carries the ball up the hill or keeps it moving in a straight line. Credit: M Run via WikiCommons CC BY-SA 4.0
Of course, we see things change their state of motion every day. You car speeds up and slows down, you turn your body left to go around the corner, and baseballs eventually fall to the ground. What makes an object change its state of motion? An object only changes its state of motion when acted upon by a force. When an object is acted on with a non-zero force, it changes its state of motion. This is called acceleration. Think of it this way: An object in moving through deep space will continue moving in a straight line unless some force can push it around and change its state of motion. Changing direction, slowing down, and speeding up all involve a change in a state of motion, and so count as acceleration and require the application of some force. Speaking of forces…
Gravity
The second component that explains projectile motion is gravity. Everyone knows how gravity works: it is the thing that keeps us on the ground down here and the moon in the sky up there. Every object exerts some gravitational pull on every object around it. The more massive the object, the stronger its gravitational pull is. Gravitational attraction is the main thing that keeps the planets in the solar system in their orbits around the sun.
Mathematically, gravity can be described as a force, and so it can change an object’s state of motion. Gravity causes a body to accelerate downward at a particular rate. When you let go of an object, gravity causes it to fall towards the ground. The longer the ball falls, the more it will be accelerated under gravity. The exact strength of gravity depends on the planet. On Earth, the strength of gravity accelerates bodies downward at a speed of about 9.8 m/s2. This means for any free falling body on Earth, its downward velocity increases by 9.8 m/s every second it is falling.
How do gravity and inertia explain the motion of the baseball through the air? Projectiles have two aspects of motion, a horizontal (x) and vertical (y) aspect. Since the two components of motion are perpendicular to each other, they can be analyzed independently of each other. Lets separately consider the horizontal and vertical components of the ball’s motion (assume that air resistance is negligible).
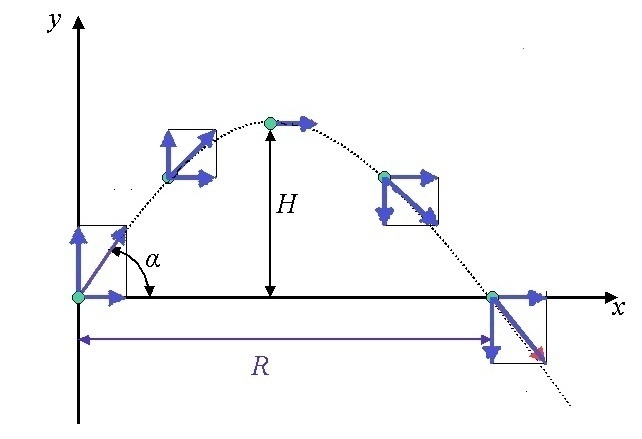
At each moment in its path, the ball has both a horizontal and vertical component of motion. Credit: Ayush via WikiCommons CC BY-SA 4.0
Horizontal
When it is thrown, the ball has some initial horizontal velocity, meaning that it is moving horizontally at some rate. Since gravity only acts downward, the ball’s horizontal state of motion is not affected by gravity (or any other force). Thus, according to the law of inertia, a projectile maintains its horizontal velocity through the entire flight. Thus, if one knows the initial horizontal velocity of the projectile then they also know the final horizontal velocity because the two are exactly the same.
Vx initial = Vx final
If the baseball has an initial horizontal velocity of 3 m/s, then at each point during its flight its horizontal velocity is also 3 m/s.
If we want to know the entire horizontal distance a projectile has traveled, all we need is the horizontal velocity and the amount of time the projectile was in the air.
DH = Vx0 × time
So if our baseball has an initial horizontal velocity 3 m/s and is in the air for 12 seconds, we know that it covered a total horizontal distance of (3m/s)(12) = 36 m.
Vertical
What about the vertical component? This case is a bit trickier because of the presence of the constant downward force of gravity. We know that the force of gravity changes the initial vertical velocity by an amount every second the object is in flight. This means that the vertical component of velocity is changing by some constant rate every second. The rate is the acceleration due to gravity. Say our initial vertical velocity is 0. On Earth, acceleration from gravity is −9.8 m/s (the negative is because gravity acts downward). Then for every second: the vertical velocity decreases by 9.8 m/s
| Time (seconds) | Velocity (m/s) |
| 0 | 0 m/s |
| 1 | -9.8 m/s |
| 2 | -16.9 m/s |
| 3 | -29.4 m/s |
| 4 | -39.2 m/s |
Mathematically, the vertical velocity at any given point during the flight can be given by:
Vy = Vy0−gt
Where g is the acceleration from gravity.
How about the vertical height? If you have taken any math classes, then you know that the formula for the vertical distance of a ball dropped from rest is just ½(acceleration)(time)2
DV = ½at2
If we factor in the initial vertical velocity of a 2-D projectile, the final expression to determine the vertical distance at a given point is:
DV = Vy0t−½at2
In our case, a is the acceleration due to gravity g, so we get:
DV = Vy0t−½gt2
Let’s look at some sample problems to practice using these formulas:
Q1.) A cannonball is shot off of a cliff with an initial horizontal velocity of 13 m/s and a vertical velocity of 7 m/s. Find (i) the vertical velocity, at 4 seconds (ii) the horizontal distance after 6 seconds, and (iii) the vertical height at 3 seconds.
Answer: Starting with (i) we can answer the questions as follows.
(i) The vertical velocity is just equal to the initial velocity minus the change due to the acceleration of gravity over time. When t=4:
Vy = Vy0−gt
Vy = 7m/s−(9.8m/ss)(4s)
Vy = -32.3 m/s
After 4 seconds, the vertical velocity is -32.3 m/s. The value is negative because the cannonball is going down.
(ii) Remember that the horizontal distance covered by a projectile is just equal to the horizontal velocity times the amount of time in the air. In our case after 6 seconds:
DH = Vx0t
DH = (13m/s)(6s)
DH = 78 meters.
After 6 seconds, the cannonball will have traveled 78 meters.
(iii) The vertical displacement at 3 seconds is just equal to the product of initial velocity and time minus the change in displacement over time.
DV = Vy0t−½gt2
DV = (7m/s)(3)−½(9.8m/s2)(3)2
DV = 21−44.1
DV = −23.1.
The negative simple means that the cannonball will be 23.1 meters below the lip of the cliff after 3 seconds.








