30 60 90 Triangle: Formulas, Rules And Sides

If you have taken any geometry odds are you know about the many different kinds of triangles. Triangles are the simplest shape that can exist in Euclidean space and they can be classified according to the lengths of their sides and measure of their angles. The different types of triangles are:

• equilateral triangle – all angles and side are of equal measure
• isosceles triangle – two sides are of equal measure
• scalene triangle – no sides are of equal length
• acute triangle – all angles are less than 90 degrees
• obtuse triangle – at least one angle is greater than 90 degrees
• right triangle – one angle is exactly 90 degrees

In this article, we will take a look at right triangles and special types of right triangles. Right triangles are interesting because they pop up all over mathematics in algebra, geometry, trigonometry, and physics.

TL;DR: Properties Of A 30-60-90 Triangle

A 30-60-90 right triangle is a special right triangle in which one angle measures 30 degrees and the other 60 degrees. The key characteristic of a 30-60-90 right triangle is that its angles have measures of 30 degrees (π/6 rads), 60 degrees (π/3 rads) and 90 degrees (π/2 rads). The sides of a 30-60-90 right triangle lie in the ratio 1:√3:2.

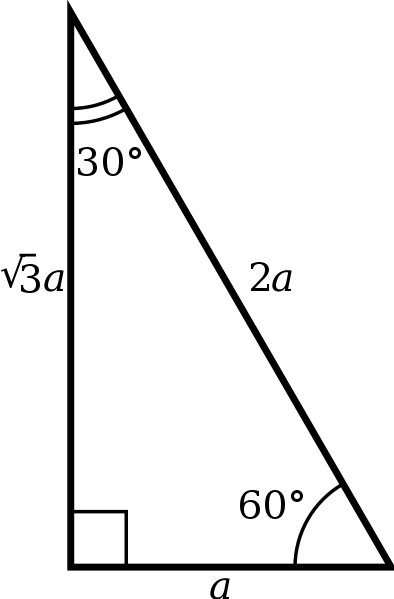
The side lengths and angle measurements of a 30-60-90 right triangle. Credit: Public Domain.

We can see why these relations should hold by plugging in the above values into the Pythagorean theorem a² + b² = c².

a² + (a√3)² = (2a)²

a² + 3a² = 4a²

4a² = 4a²

Notice that these ratios hold for all 30-60-90 triangles, regardless of the actual length of the sides. So, for any triangle whose sides lie in the ratio 1:√3:2, it will be a 30-60-90 triangle, without exception.

Right Triangles: An Overview

As stated previously, a right triangle is any triangle that has at least one right angle (90 degrees). The different parts of a right triangle are as follows.

• hypotenuse
• legs

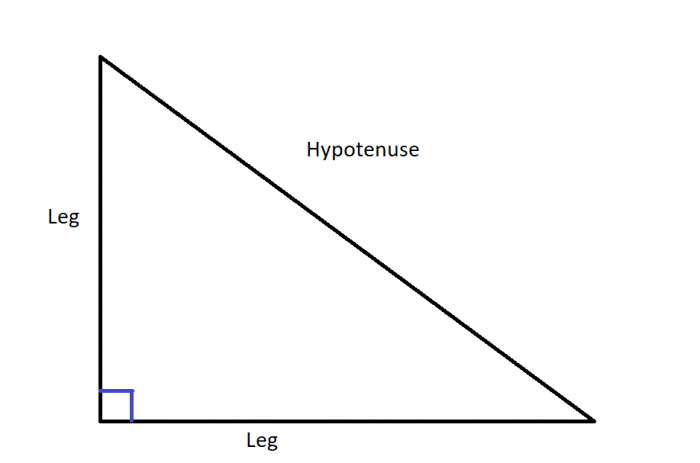
Credit: Author

The non-hypotenuse sides of a right triangle are called its legs. These are the general parts present in every right triangle. Right triangles have some very interesting properties that make them of interest to mathematicians. First and foremost is the famous Pythagorean theorem which relates the length of the different sides of a right triangle. In English, the Pythagorean theorem states:

PT: “The square of the hypotenuse of a right triangle is equal to the sum of the squares of its legs”

Mathematically, the Pythagorean theorem can be written as:

PT: a² + b² = c²

The Pythagorean theorem can be used to figure out the length of any side of a right triangle if you know the lengths of the other 2. For example, say we have a right triangle with legs of lengths 6 and 8. By the Pythagorean theorem, the length of the hypotenuse squared is equal to the sum of the squares of the individual legs:

(6)² + (8)² = c²

36 + 64 = c²

100 = c²

c = 10

A right triangle with legs of lengths 6 and 8 has a hypotenuse that is length 10. This formula is true for all right triangles, regardless of the lengths of their sides.

Humans have been studying right triangles since recorded history began. Right triangles and their properties were known to the ancient Babylonians and the ancient Egyptian, India, and China. Right triangles are most commonly associated with Pythagoras, a Greek mathematician/mystic who lived during the 6th century BCE. Although Pythagoras was well-known during his time for his geometric proofs involving triangles and their properties, it is unlikely that he actually discovered the famous mathematical theorem that bears his namesake. Rather, he was most likely a popularizer and teacher of already known mathematical concepts.

Right Triangles And The Coordinate Plane

A natural way to visualize the vertices of a right triangle is as points on the coordinate plane. Imagine the hypotenuse of a right triangle as a line that stretches diagonally from the origin of the coordinate axis:

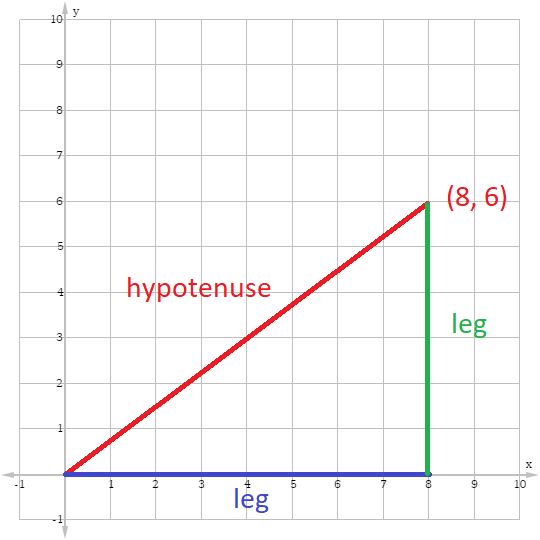
Credit: Author

Visualizing a right triangle this way makes it easy to see that the length of the two legs of a right triangle are just equal to the x- and y-coordinates of the point where the hypotenuse terminates. So, a single point on the coordinate plane encodes information about a right triangle formed by drawing a line from the origin to that point.

Visualizing a right triangle this way also explains why the distance formula holds. Recall that the distance formula is a way to calculate the distance between two points on the coordinate plane (x₁, y_y) and (x₂, y₂). The distance formula states:

D = √((x₂−x₁)² + (y₂−y₁)²)

Notice that when one of these points is the origin (0, 0), the formula simplifies into the Pythagorean theorem. So, one can understand the distance formula in terms of constructing a right triangle that connects two points in the coordinate plane.

Angles Of A Right Triangle

The angles of right triangles also have some interesting properties. Notice first that for all right triangles, the sum of the non-right angles is always equal to another right angle. This is because triangles necessarily have interior angles that add up to 180 degrees. If one of those angles is 90 degrees (as is the case in a right triangle), then the other two angles must be complementary and add up to 90 degrees.

Right triangles can also be understood in the context of the trigonometric functions sine, cosine, and tangent. For any randomly chosen angle A in a right triangle, the other parts can be defined as:

• the opposite side is directly across from the angle
• the adjacent side is directly next to the angle
• the hypotenuse is the side directly opposite the right angle

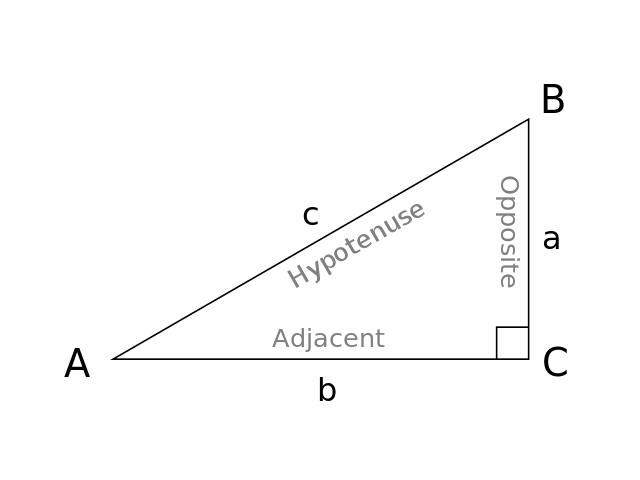
Credit: Public Domain

The trig function sine, cosine, and tangent are defined in terms of the ratios that hold between the angles and the sides of a right triangle. The trig functions are defined as:

• sinA = opposite/hypotenuse
• cosA = adjacent/hypotenuse
• tanA = opposite/adjacent

The trig functions take angle measurements as their inputs and give ratios as their outputs. Trig functions are notoriously difficult to calculate by hand, but there are a few special right triangles that make computing certain values of the trig functions much easier and intuitive.

Special Right Triangles

Among the infinitely many right triangles, there are a few that have unique properties that make computing the value of the different trig functions simple. The two main kinds of “special” right triangles are 45-45-90 triangles and 30-60-90 triangles. There are also what are known as Pythagorean triples, right triangles who side lengths are integer values.

45-45-90 Triangles

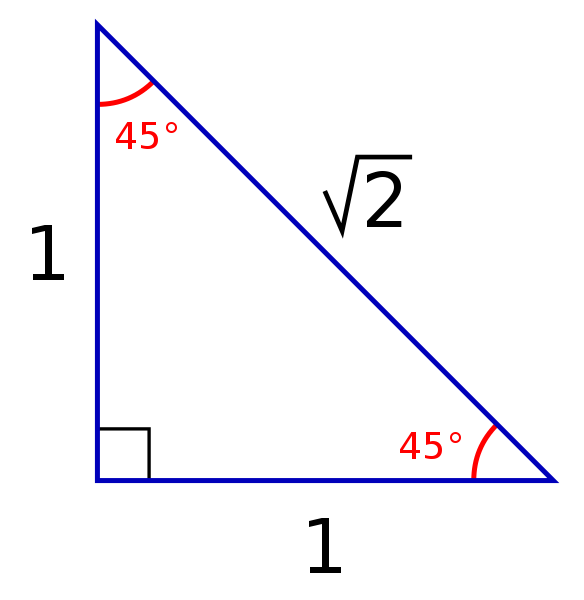
Credit: Public Domain

A 45-45-90 triangle is any right triangle where its two non-right angles are both 45 degrees. The defining characteristic of a 45-45-90 triangle is that its two legs are equal length. A 45-45-90 triangle can be seen as the triangle that is produced by cutting a square across its diagonal.

The sides of a 45-45-90 triangle lie in the ratio 1:1:√2. Knowing these ratios makes computing the values of trig functions much easier. Since the two non-right angles of a 45-45-90 triangle are both 45 degrees, we know the values of the trig functions when the argument is 45 degrees. Specifically, we know:

sin(45) = 1/√2 = 0.7071…

cos(45) = 1/√2 = 0.7071…

tan(45) = 1/1 = 1

Since 45 degrees = π/4 radians, we know that

sin(π/4) = 0.7071…

cos(π/4) = 0.7071…

tan(π/4) = 1

30-60-90 Right Triangles

The other most well known special right triangle is the 30-60-90 triangle. In a 30-60-90 triangle, the two non-right angles are 30 and 60 degrees.

Credit: Public Domain

A 30-60-90 triangle has sides that lie in a ratio 1:√3:2. Knowing these ratios makes it easy to compute the values of the trig functions for angles of 30 degrees (π/6) and 60 degrees (π/3). Specifically:

sin(30) = 1/2 = 0.5

cos(30) = √3/2 = 0.8660…

tan(30) = 1/√3 = 0.5773…

sin(60) = √3/2 = 0.8660…

cos(60) = 1/2 = 0.5

tan(60) = √3/1 = 1.7320…

The 30-60-90 right triangle is special because it is the only right triangle whose angles are a progression of integer multiples of a single angle. If angle A is 30 degrees, the angle B = 2A (60 degrees) and angle C = 3A (90 degrees).

Pythagorean Triple

A Pythagorean triple is any set of positive integer values a, b, and c that satisfy the Pythagorean theorem a² + b² = c². In geometric terms, a Pythagorean triple corresponds to a right triangle in which all the side lengths are equal to a positive integer. The simplest example of a Pythagorean triple is (3, 4, 5)

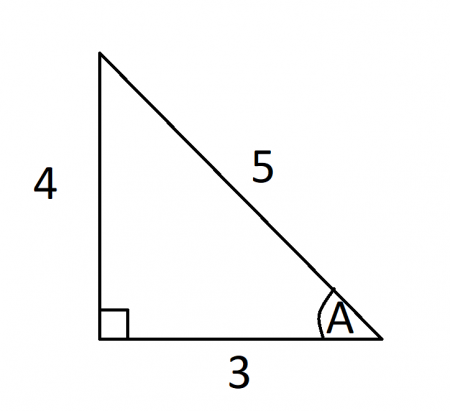
Credit: Author

Notice that these three numbers satisfy the Pythagorean theorem: 3² + 4² = 5². There are an infinite amount of Pythagorean triples which corresponds to an infinite amount of right triangles with sides of integer lengths. Not all of these right triangles are unique though; for example, a 6-8-10 triangle is essentially the same thing as a 3-4-5 triangle, the former is just an integer multiple of the latter (multiplied by 2). A primitive Pythagorean triple is any set of numbers a, b, c, that satisfy the Pythagorean theorem AND are also coprime; meaning they do not share any factors in common. (3, 4, 5) is the first primitive Pythagorean triple with the next being (5, 12, 13).

Notice that if a triangle is a 45-45-90 triangle, its sides cannot be a Pythagorean triple. This is because the sides of a 45-45-90 triangle do not form a ratio of positive integers. The ratio of the sides in a 45-45-90 triangle is 1:1:√2. √2 is not an integer (it is not even a rational number) so no 45-45-90 triangle can have sides that are integer length. By similar reasoning, a 30-60-90 triangle can also never be a Pythagorean triple because √3 is not an integer.