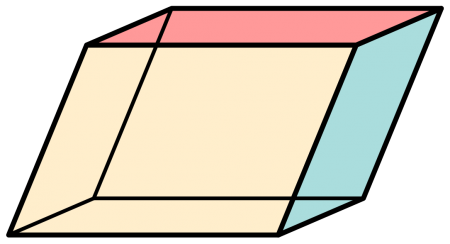
In geometry, a parallelogram is a convex quadrilateral polygon that is characterized by having 2 sets of parallel sides. In other words, a parallelogram is a 4-sided figure in which opposite pairs of sides lie parallel to each other. Some key properties of parallelograms include:
- opposite sides are parallel
- opposite sides are congruent
- opposite angles are congruent
- adjacent angles are supplementary
- diagonals bisect each other.
- sum of squares of sides equals sum of squares of diagonals (parallelogram law)
The unique properties of parallelograms make them very useful in geometry, engineering, and science. Parallelogram-shaped devices are used in engineering to lift heavy loads and build large structures. In physics, parallelograms are used to model individual force components and to describe vector addition. The three-dimensional analog of a parallelogram is called a parallelepiped.
Definition Of A Parallelogram
At its simplest, a parallelogram is any quadrilateral with 2 pairs of parallel opposite sides. This definition includes various kinds of shapes. All squares and rectangles are parallelograms, they are just special parallelograms where all interior angles are right angles. A rhombus is a special kind of parallelogram in which all four sides are equal length.
Normally when people hear the word “parallelogram” they think of a rhomboid—a parallelogram with non-congruent pairs of opposite sides.
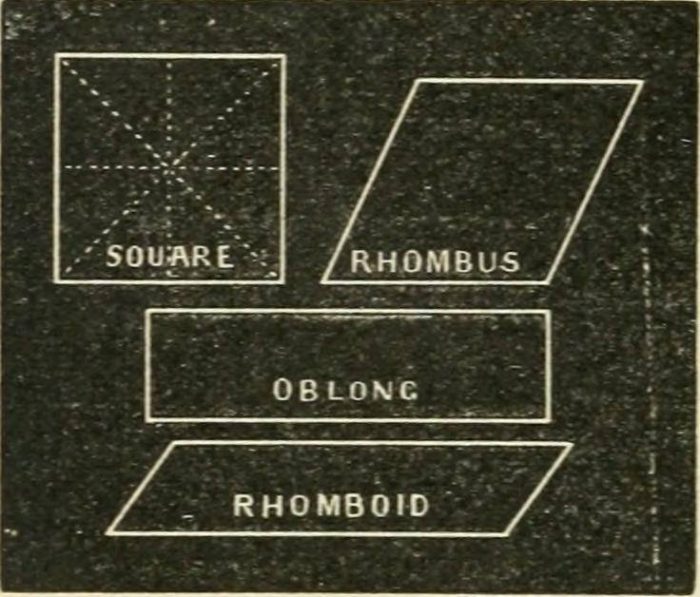
The 4 kinds of parallelograms. Credit: Flickr via Public Domain
For our purposes, most pictures in this article will be of rhomboids, but keep in mind that the lessons we cover apply to the other types of parallelograms as well.
From this very simple definition of a parallelogram as a quadrilateral being composed of opposite pairs of parallel lines, we can deduce a key set of properties that all parallelograms must have by geometric necessity.
Unique Properties Of Parallelograms
1. Opposite Sides Are Congruent
One property of a parallelogram is that its opposite sides are equal in length. We can prove this simply from the definition of a parallelogram as a quadrilateral with 2 pairs of parallel sides. Consider parallelogram ABCD with a diagonal line AC.:
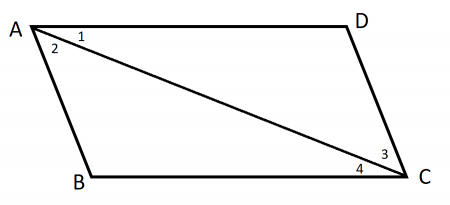
Credit: Author
The following is a proof showing that opposite sides of a parallelogram are congruent.
| Statement | Reason | ||
| 1 | □ ABCD | 1 | Given |
| 2 | Draw AC | 2 | Two points determine a line |
| 3 | AB||CD; AD||BC | 3 | Def. of a parallelogram |
| 4 | ∠1 ≅ ∠4; ∠2 ≅ ∠3 | 4 | 2 || lines cut by a trans. line, alternate interior angles are congruent |
| 5 | AC ≅ AC | 5 | Reflexive (Identity) |
| 6 | ΔABC ≅ ΔCDA | 6 | ASA; two triangles sharing congruent angle, side, angle are congruent triangles |
| 7 | AB≅DC; AD≅BC | 7 | Corresponding parts of congruent triangles are congruent (CPCTC). Q.E.D. |
Essentially this proof tells us that splitting a parallelogram with one of its diagonals creates two congruent triangles.
2. Opposite Angles Are Congruent
Another property of parallelograms is that they have opposite pairs of congruent angle. This means that pairs of angles directly across from each other are of equal magnitude. The following proof demonstrates:

Credit: Author
| Statement | Reason | ||
| 1 | □ ABCD | 1 | Given |
| 2 | Draw AC | 2 | 2 points make a line |
| 3 | AB||CD; AD||BC | 3 | Def. of a parallelogram |
| 4 | ∠1 ≅ ∠4; ∠2 ≅ ∠3 | 4 | Alternate interior angles |
| 5 | ∠1+∠2 = ∠3+∠4 | 5 | Addition of equalities |
| 6 | ∠DAB ≅ ∠BCD | 6 | Substitution |
| 7 | AC = AC | 7 | Reflexive property |
| 8 | ΔABC ≅ ΔCDA | 8 | ASA |
| 9 | ∠D ≅ ∠B | 9 | CPCTC. Q.E.D. |
So, we have proven that the opposite angles of a parallelogram are congruent.
3. Adjacent Angles Are Supplementary
For parallelograms, the adjacent angles are supplementary to each other (add up to 180°). We can prove this with the following:

Credit: Author
| Statement | Reason | ||
| 1 | □ ABCD | 1 | Given |
| 2 | Draw AC | 2 | 2 points make a line |
| 3 | AB||CD; AD||BC | 3 | Def. of a parallelogram |
| 4 | ∠A supp ∠B; ∠B supp ∠C; ∠C supp ∠D; ∠D supp ∠A | 4 | If 2 || lines are cut by a trans. , interior angles on the same side of the trans. are supplementary. Q.E.D |
Therefore, adjacent angles of a parallelogram are supplementary.
4. Diagonals Bisect Each Other
A diagonal in a polygon is a straight line drawn between pairs of non-adjacent angles. A parallelogram has 2 diagonals. These diagonals also bisect each other, meaning that they intersect at each other’s midpoints. We can prove this with the following:
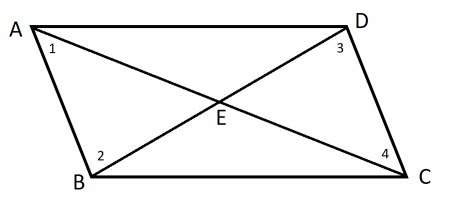
| Statement | Reason | ||
| 1 | □ ABCD | 1 | Given |
| 2 | AB||CD; AD||BC | 2 | Def. of a parallelogram |
| 3 | ∠1 ≅ ∠4; ∠2 ≅ ∠3 | 3 | Alternate interior angles are congruent |
| 4 | AB ≅ DC | 4 | Opposite sides of parallelogram are congruent |
| 5 | ΔABE ≅ ΔCDE | 5 | ASA |
| 6 | BE ≅ DE; CE ≅ AE | 6 | CPCTC |
| 7 | BD bisects AC; AC bisects BD | 7 | A segment bisector intersects line segment to make two congruent segments. |
5. Parallelogram Law
The parallelogram law states that the sum of the squares of the sides is equal to the sum of the squares of the diagonals. Mathematically, for the following parallelogram:
2
The parallelogram law states:
(AB)2 + (BC)2 + (DC)2 + (DA)2 = (AC)2 + (BD)2
Since parallelograms have congruent opposite sides (AB = DC and BC = DA), the parallelogram law can be rewritten as:
2(AB)2 + 2(BC)2 = (AC)2 + (BD)2
The parallelogram law can be proven as such:
| Statement | Reason | ||
| 1 | (AB)2 + (BC)2 – 2(AB)(BC)cos(∠ABC) = AC2 | 1 | Law of cosines |
| 2 | 180 – ∠ABC = ∠DCB | 2 | Adjacent angles are supplementary |
| 3 | AB = CD; BC = AD | 3 | Opposite sides of parallelogram are congruent |
| 4 | (CD)2 + (AD)2 – 2(CD)(AD)cos(180 – ∠ABC) = BD2 | 4 | Law of cosines |
| 5 | cos (180 – x) = -cos(x) | 5 | Trig identity |
| 6 | (CD)2 + (AD)2 + 2(CD)(AD)cos(∠ABC) = BD2 | 6 | Substitution, 4 |
| 7 | 2(AB)2 + 2(BC)2 = (AC)2 + (BD)2 | 7 | Adding and simplifying. 1, 3, and 6. Q.E.D |
So we have proven that the sum of the squares of the sides of a parallelogram is equal to the sum of the square of the diagonals. In the case of a parallelogram where the angles are right angles (i.e. a rectangle), this formula simplifies down into the Pythagorean theorem a2 + b2 = c2
Other Properties Of Parallelograms
Area
The formula for the area of a parallelogram is the same as the formula for the area of a square or rectangle.
b x h
Where b is the base and h is the height. Why does this work for parallelograms though? Consider the following illustration.
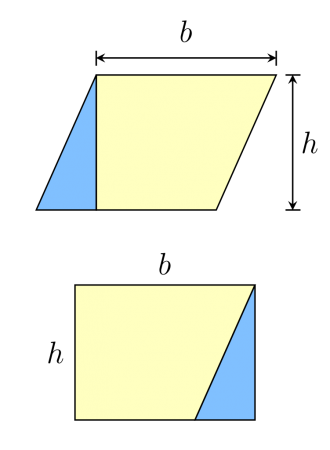
Credit: WikiCommons CC0 1.0
Drawing a line perpendicular from the base to one of the terminal points of the side gives you a right triangle with one of the sides equal to the height. You can transpose this triangle from the left side to the right side to make a normal rectangle. Since the total area does not change while you move the triangle, the entire area is just the base times the height. In other words, you can always cut up a parallelogram into a right triangle and a trapezoid and rearrange the pieces into a rectangle.
Parallelograms And Forces
Parallelograms are useful in physics because they can be used to model the individual components of forces acting on a body. For example, say that some particle has two forces acting on it in different directions. These forces can be represented by arrows that show the magnitude and direction of the force:
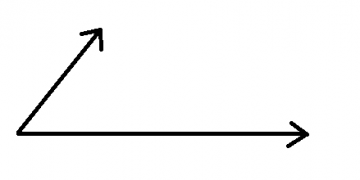
What is the total force acting on the particle? The two force vectors should combine into a new third vector that is a combination of the two. The resultant vector would look like this:
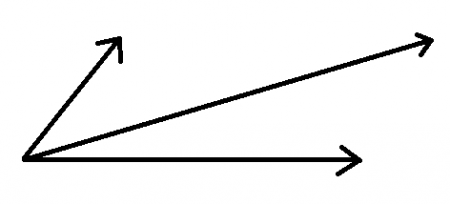
Notice anything familiar about this shape? if we connect the rest of the dots:
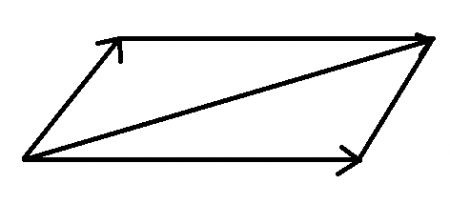
The resultant vector forms the diagonal of a parallelogram with sides that are the individual vector components. The is called that parallelogram force law and is extremely useful in physics and engineering, fields where vector addition is common.
This particular law does not only hold with forces, but with any kinds of vector quantity, such as velocity or acceleration. The combination of two vectors can always be represented as a parallelogram with sides equal to the individual vector components.
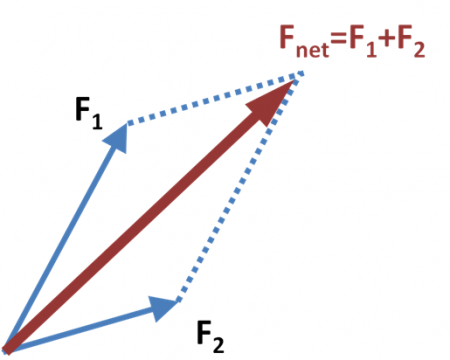
Credit: B. Ohare via WikiCommons CC BY-SA 3.0
The first person to prove this fact about forces was Isaac Newton in his Principia Mathematica. This same reason is why parallelograms are used in engineering to transfer forces. The fact that forces happen to combine to form a parallelogram does not seem to be a mathematical law about how vectors are defined, but a peculiar empirical fact about the world we live in.
3-D Parallelogram
As with many 2-D shapes, a parallelogram has a corresponding analog in 3 dimensions. The 3-D analog of a parallelogram is called a parallelepiped. A parallelepiped consists of 6 equal parallelogram faces. The parallelepiped is to the parallelogram as the cube is to the square, or as the sphere is to the circle. A parallelepiped can also be considered a prism with a parallelogram base.
The formula for the volume of a parallelepiped is the same as the formula for the area of a 2-D parallelogram. Simply multiply the area of the base by the height to find the volume.
A = B × h
In summary, a parallelogram is a quadrilateral that contains two opposite pairs of parallel sides. Parallelograms have several characteristic properties that fall directly out of their definition as a quadrilateral with opposite pairs of parallel sides. the properties of a parallelogram are:
- opposite sides are congruent
- opposite angles are congruent
- adjacent angles are supplementary
- diagonals bisect each other
- sum of squares of sides is equal to sum of squares of diagonals.
The area for a parallelogram is exactly the same as that of a rectangle, base times the height. This is because any parallelogram can be split into a trapezoid and right triangle that can be rearranged into a rectangle.
Parallelograms can be used to represent the addition of vector components. The resultant force is equal to the diagonal of a parallelogram with sides equal to the individual force components. This parallelogram law can be used to add all kinds of vectors, not just forces.