What Is A Rhombus?

A rhombus (rhombi pl.) is the name for a special kind of quadrilateral, one in which all 4 sides are of the same length. For this reason, a rhombus is also sometimes called an “equilateral quadrilateral,” as it is a 4-sided figure with sides of equal length. The rhombus is also called a diamond, as its common presentation looks like the diamond suit on a standard 52-card deck of playing cards.

Essentially, a rhombus is what you would get if you grabbed opposite corners of a square and pulled them apart while keeping the lengths of the sides constant. The name “rhombus” comes from an ancient Greek word meaning “to turn round and round.” Both Euclid and Archimedes described a rhombus as the shape of the profile of 2 solid circular cones that share a base.

Basic Properties Of A Rhombus

Like all geometric shapes, rhombi are distinguished by a special set of characteristics. In short, a rhombus can be defined as a special case of the parallelogram, one in which all 4 sides have the same length. Thus, all rhombi are parallelograms, as well as kites— quadrilaterals that have 2 pairs of equal sides that are adjacent to each other. Further, a square is a special kind of rhombus, one in which all angles are right angles (so a square is a kind of kite and a kind of parallelogram as well).

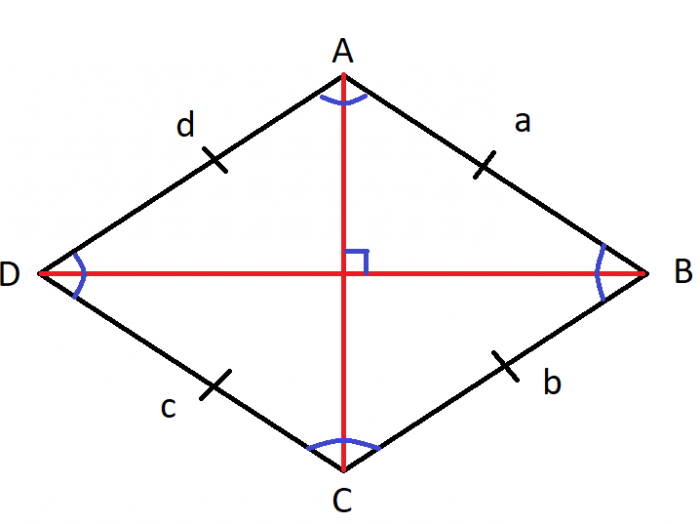
Credit: Author.

Here are some geometric properties of a rhombus:

•  Sides a, b, c, and d are congruent; that is, they have the same size and shape.
• Opposite pairs of sides are parallel: a and c are parallel, b and d are parallel).
• Opposite angles are equal to each other: ∠A = ∠C and ∠B = ∠D
• Adjacent angles are supplementary: ∠A+∠B = 180°, ∠C+∠D = 180°
• Diagonals (red lines) bisect their respective angles: Line AC cuts ∠A and ∠C each into two equal smaller angles, line BD cuts ∠B and ∠D into two equal smaller angles.
• Diagonal lines are perpendicular: Lines AC and BD intersect at a 90° angle.
• Diagonal lines intersect at their midpoints.
• The midpoints of the 4 sides inscribe a rectangle.

A rhombus has a perfect symmetry across its vertical and horizontal axis, meaning that if we flipped it backward or upside down, we would get the same shape. We can prove this too. Drawing a line down the vertical axis of a rhombus divides it into two congruent triangles. (likewise for the horizontal axis) Since congruent triangle are similar in all aspects, it follows that the corresponding sides and angles of the left triangle and right triangle are exactly similar in all aspects

Every rhombus consists of two pairs of parallel lines that intersect at 4 points, making every rhombus a parallelogram. Like every other quadrilateral, the interior angles of a rhombus add up to 360°. To see why, consider what would happen if we inscribed a rhombus inside of an ellipsoid, like so:

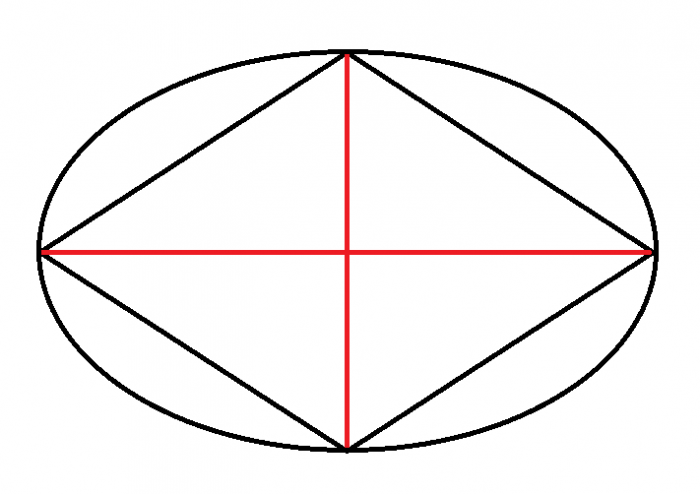
Credit: Author

Imagine a person starting at the rightmost point where the rhombus and ellipsoid intersect and traveling to each point by following the curve of the path traced out by the ellipse. Once they have gone all the way around once, the person will have made one complete rotation, corresponding to a 360° arc. Alternatively, if a person were to stand at the intersection of the two diagonals (red lines) begin by looking at the rightmost vertex and turning to each subsequent vertex, they would complete 4 90° rotations before they were looking at the starting vertex again.

Rhombi are tangential quadrilaterals, meaning that for every rhombus there exists an inscribed circle such that every side of the rhombus is tangential to that circle

In terms of the Cartesian plane, the properties of a rhombus can be encoded by the algebraic expression:

|x/a|+|y/b| = 1

The vertices of the rhombus are located at points (±a, 0) and (±b, 0). Any graphed rhombus will have points that satisfy this equation.

Area Of A Rhombus

The area of any rhombus can be calculated in the same way as any parallelogram, multiply the base times the height. In this case, the base is just equal to the length of the side of the rhombus, so if you know at least one side, you know the base. The height of a rhombus is equal to the length of a line drawn perpendicular from one side to a non-adjacent side

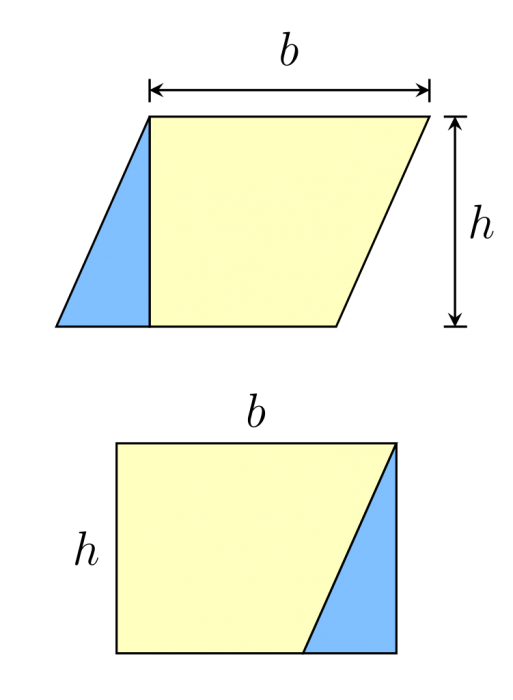
Credit: WikiCommons CC0 1.0

Just like a parallelogram, a rhombus can be seen as a rearranged rectangle. Drawing a line perpendicular from one side to reach the opposite angle creates a right triangle. This right triangle can then be “cut” out and moved to the other side to complete the rectangle. This property is what allows the area of a rhombus (and parallelograms more generally) to be calculated in the same manner as a rectangle.

Alternatively, One can calculate the area of a rhombus if one knows the lengths of the diagonal. A rhombus has the interesting property that its area is exactly equal to half the product of the length of its 2 diagonal lines. So, if we have a rhombus whose diagonal lines are 6cm and 12cm, we know that the area of the rhombus is equal to the product of these two values divided by 2: (12×6)/2 = 36; A rhombus with diagonals of 12cm and 6cm has a total area of 36cm².

The area of a rhombus can also be expressed as the base squared multiplied by the sin of any angle:

Area = b² × sinα = b² sinβ

Thus, if one knows the sides and any single angle of the rhombus, they can calculate what the area must be. For example, a rhombus with a side length of 4 cm and a vertex angle of 60° would be

Area = 4² × sin60 ≈ 13.86 cm²

Diagonals Of A Rhombus

If one knows the side and vertex angle of a rhombus, they can figure out the lengths of the diagonals according to the following equations, where p and q stand for the diagonals and a stands for the side:

p = a√(2+2cosθ)

q = a√(2−2cosθ)

These two formulas follow as a direct result of the law of cosines, a law in trigonometry that states the sides of a triangle are related to the cosine of one of its angles.

Further, the length of the diagonals can be related to the lengths of the sides by the expression:

4a² = p² + q²

This expression is a consequence of the law of parallelograms, a law that states the sum of the squares of the 4 sides of a parallelogram are equal to the sum of the squares of its diagonals. This particular mathematical equation is just a special case of that bigger law, a case where the lengths of all 4 sides are equal.

Shapes Related To The Rhombus

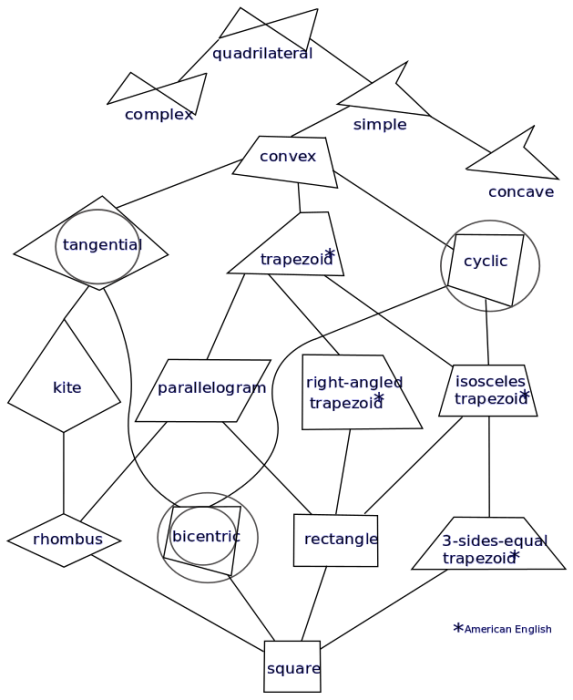
Credit: “Quadrilateral Hierarchy” Alexgabi via WikiCommons CC BY-SA 3.0

A rhombus is a kind of quadrilateral, the general name for a closed convex polygon with exactly 4 sides. Other kinds of quadrilaterals include rectangles, trapezoids, kites, squares, and parallelograms. One property that all quadrilaterals share in common is that their interior angles necessarily add up to 360°. Starting from the most general kind of quadrilateral, the different 4-sided shapes have a hierarchy where each successive shape can be seen as a special instance of the previous shape.

• Convex quadrilateral: No angle are greater than 180°
  • Tangential quadrilateral: can have a circle inscribed in it.
  • Cyclical quadrilateral: can be inscribed in a circle.
• Irregular quadrilateral: No sides are parallel
• Trapezoid: Quadrilateral where at least one pair of sides are parallel
  • Scalene trapezoid: trapezoid in which all sides are different lengths
  • Right trapezoid: trapezoid with at least one right angle.
  • Isosceles trapezoid: trapezoid where one pair of sides are parallel, and the base angles are equal.
• Parallelogram: Quadrilateral with both pairs of sides parallel to each other.
• Kite: Quadrilateral with two pairs of adjacent sides that are equal in length.
  • Right Kite: Kite with two opposite right angles
• Rhombus: Parallelogram when each side is equal in length.
• Rectangle: Parallelogram where each angle is a right angle (90°)
  • Oblong: An old term for a rectangle that is not a square
• Square: Rectangle where all sides are of equal length.

All quadrilaterals have two lines called diagonals, that run from angle to opposite angle. The diagonals of quadrilaterals encode a number of properties of the shape. In fact, there is a single general expression that can be used to calculate the area of any convex quadrilateral that only requires one to know the lengths of the diagonals. This expression is:

Area = ½pq × sinθ

Where p and q are the lengths of the diagonals and θ is the angle between them. This formula can be used to compute the area of any convex quadrilateral, rhombus included.

In summary, a rhombus is a special type of parallelogram, one in which all the sides are equal length. A rhombus has a pair of diagonals perpendicular to each other, and diagonals that bisect their angles. In a rhombus, pairs of opposite angle are equal and pairs of adjacent angles are supplementary. The area of a rhombus can be calculated just like other parallelograms, multiply the base by the height. Alternatively, the area of a rhombus is equal to half of the product if its diagonals.