Does Not Equal Sign: What Does ≠ Mean And How To Type It?

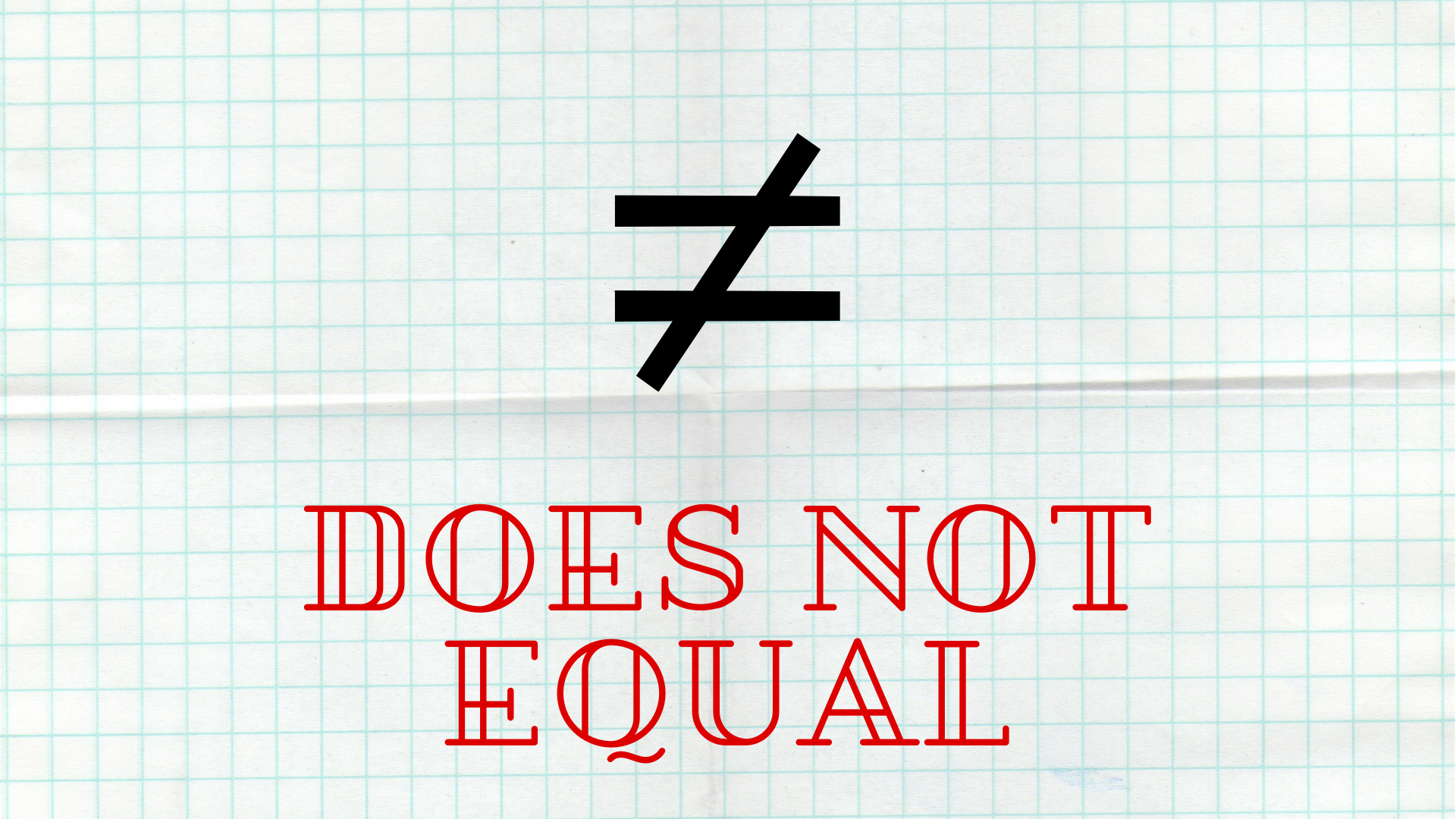
The “does not equal” or “is not equal to” sign is an expression of the inequality between two different numbers, variables, integers, or concepts. It is a variation on the equals sign, which is an expression of mathematical equality. The not equals sign can be typed using the following commands: U+2260; 2260, Alt+X in Microsoft Windows. You can also ascertain the Unicode value of ≠ and then use a Unicode input tool to create your own keyboard shortcuts.

Let’s see how the not equals sign is used in math and in other contexts, as well as how it relates to the regular equals sign.

“Mathematics is not about numbers, equations, computations, or algorithms; it is about understanding.” — William Paul Thurston

What Is Unicode/ASCII?

Photo: By Unknown – de:Bild: Unicode logo.jpg, Public Domain, https://commons.wikimedia.org/w/index.php?curid=12627185

Special characters like the “does not equal” or inequality symbol are typed with certain Unicode characters. Unicode is a system of standardization for the encoding and display of text characters and symbols. The Unicode consortium contains over 137,000 characters covering different languages, scripts, symbols, and even emojis. Unicode characters are widely used in computer software and programming languages, thanks to providing a consistent standard for operating systems and languages. UTF-8 is the primary encoding type used by the World Wide Web and it allows the display of the “≠”.

An ASCII chart from propr to 1972. Photo: By an unknown officer or employee of the United States Government – http://archive.computerhistory.org/resources/text/GE/GE.TermiNet300.1971.102646207.pdf (document not in link given), Public Domain, https://commons.wikimedia.org/w/index.php?curid=63485656

The American Standard Code for Information Interchange, or ASCII, is an older encoding standard succeeded by Unicode, though it still is in use in many places. Special Unicode and ASCII characters, characters that are not present on a keyboard, can be typed by using a series of commands, such as pressing down ALT and typing in a corresponding number for ASCII characters. Charts and character databases exist to look up special characters.

History Of The Equals Sign

The equals/equality sign is a mathematical symbol used to assert equality between two expressions. Most keyboards have a shortcut for writing the equals sign, located above the brackets on a QWERTY keyboard layout.

Image of Robert Recorde. Photo: By The original uploader was Lumos3 at English Wikipedia. – Transferred from en.wikipedia to Commons., Public Domain, https://commons.wikimedia.org/w/index.php?curid=3098302

The word “equals” is believed to come from the Latin term “æqualis” which can be translated roughly as “even”, “identical”, or “uniform”. It is believed that the equals sign was invented around 1557 by Robert Recorde. Recorde was a Welsh Mathematician who first used a much larger, wider equals sign to represent two equivalent items, calling them parallel lines or “Gemowe lines” (twin lines).  Recorde is reported to have found the act of having to repeatedly state that two values were equal to one another time consuming and irritating, developing a shorthand to convey the meaning of equivalency.

A representation of the first known equation, equivalent to 14x  + 15 = 71. Photo: By Robert Recorde – http://mathshistory.st-andrews.ac.uk/Bookpages/Recorde4.jpeg, Public Domain, https://commons.wikimedia.org/w/index.php?curid=4338503

While Recorde’s new equals sign succinctly implied equality between two values, it wasn’t widely adopted until much later. One reason that Recorde’s symbol may have been slow to catch on was that in the 16th century Latin still heavily influenced communication, and the term “aequalis” was frequently just shortened to “Ae” or “oe” if an abbreviation was required. However, Recorde had introduced English speakers to the now-famous German symbols for subtraction and addition: “+” and “-”. This gave Recorde’s equals sign some extra influence, as when combined with + and – the equals sign could easily be used to assert mathematical equations that took much longer to write out. A vertical equals sign, rather than a horizontal equals sign, may have been used throughout the 1600s, with the now universally used horizontal equal sign becoming standardized over the course of the 1700s.

“Math is the language of the universe. So the more equations you know, the more you can converse with the cosmos.” — Neil DeGrasse Tyson

It is arguable that Recorde laid the foundation for the discipline of computer science, as computer science is at its core about processing, creating, and collecting data. Recorde’s equals sign and other contributions to mathematical theory and operators gave computer scientists a ubiquitous and universally recognized symbol to assign values and assert a quality. Beyond that, Rercorde helped introduce the world at large to concepts of data manipulation and quantification, with theories and instructions on applying mathematics to various domains such as navigation, commerce, land surveying, and astronomy.

Usage Of The Equals Sign

In math, using the equals sign asserts that two statements or variables are equivalent to one another. However, the equals sign is often used in other fields, such as in computer programming. FORTRAN is believed to be the first computer language to make use of the equals sign, with the sign being included in revisions to FORTRAN in 1957. In computer programming languages in general, the equals sign doesn’t exactly mean two things are equivalent, instead, it functions as an assignment operator, setting the value of some statement to a following statement.

Photo: John Sauter via Wikimedia Commons, Public Domain

Other computer languages may use the equals sign with the traditional “equivalency” meaning. Examples of both types of use for the equals sign can be found in modern programming languages. Languages like Perl, Python, and C  continue to use the equals sign as an assignment operator, while languages like Eiffel, Asa, and APL use the equals sign to indicate equivalency.

Programming languages that don’t use the equals symbol as a statement of equality have other methods of handling this equality comparison. For instance, Python uses a double equals sign (“==”) as a comparison operator since the single equals sign is used as an assignment operator. Likewise, PHP uses three equals sign to make statements about value equality, showing that the expressions have equal values and share the same data type. Meanwhile, Javascript uses the triple equals sign to indicate “equality without type coercion”.

“Mathematics possesses not only truth, but a supreme beauty — a beauty cold and austere, like that of sculpture.” — Bertrand Russell

Other usages of the equals sign include the usage of the sign in chemistry, where it signals the presence of a double bond between atoms. The field of linguistics sometimes uses the equals sign to denote clitic boundaries, with the sign coming in between the word the clitic is attached to and the clitic itself.

Note that the sign may occasionally be used to connect steps of mathematical operations together in a non-standard way. People will occasionally write out operations like this:

2 + 3 = 5 + 6 = 11 + 4 = 15

The intention here is to represent adding the first two numbers together followed by adding another number. Yet this is incorrect notation. To represent this properly, one should represent the different computations with commas in between them:

2 + 3 = 5, 5 + 6 = 11, 11 + 5 = 15

Not Equals And Other Equals Sign Variants

The not equals sign (≠) can be written using certain Unicode commands such as U+2260; 2260,Alt+X in Microsoft Windows. However, due to the difficulty in using such commands, a number of alternatives are frequently employed to denote inequality. An exclamation point combined with the equals sign, or a slash combined with an equals sign, are frequently used to stand in for the not equals sign (“!=” and “/=”). These stand-ins for the inequality symbol are frequently used in programming languages because they are restricted to ASCII characters and the main characters found on a keyboard, and for this reason, they typically use “~=”, “/=”, “!=”, or “<>” as a statement of inequality.

While there is some disagreement about the precise origin of the  “!=”“symbols for the “not equals” sign, one hypothesized origin for the symbol is that it comes from the C computer programming language, as earlier languages like FORTRAN used “.ne” to assert that two values were not equal to one another.

Beyond the not equals sign, there are other variants of the equals sign. The “≈” is used to denote the approximate equivalency of two terms, to show that two terms are nearly but not exactly equivalent to one another. This approximately equal symbol has its own variants, which include a single “~” to denote proportionality. The “~” is also occasionally used to stand in for the approximately equal symbol, due to the difficulty that many people have typing Unicode characters.

“Do not worry about your difficulties in Mathematics. I can assure you mine are still greater.” — Albert Einstein

A triple bar, instead of a double bar like the equals sign has, is sometimes used to indicate definitions for mathematical terms, indicating identities for values/variables, and congruence relations in algebraic operations. The isomorphism, “≅”, is frequently utilized to indicate that geometric figures are congruent or to denote isomorphic algebraic structures.

Other Mathematical Operators

What follows is a list of other mathematical operators:

• “+” stands for addition.
• “-” stands for subtraction.
• “*” or “x” denotes multiplication.
• “^” denotes exponentiation
• “!” denotes a factorial
• “/” denotes division or the solution for a linear equation

In linear algebra or computer science, these mathematical operators may have different definitions. When manipulating matrix and string arrays, the following operators have these definitions:

• “!”  represents matrix vertical concatenation
• “~”  represents matrix horizontal concatenation
• “$| “ represents string array vertical concatenation
• “$~ “ represents string array horizontal concatenation.