What Are The Spring Constant Units?

The spring constant is a mathematical parameter present in Hooke’s law, the mathematical law that describes the stored potential energy of a coiled or stretched spring. Hooke’s law, named after the English natural philosopher Robert Hooke who originally formulated the principle, states that the distance a spring is stretched or compressed is directly proportional to the applied force. Hooke’s law can be expressed as:

F_s = −kx

Where F_s is the required force and x is the distance. The spring constant, written as k in the equation, can be seen as a measurement of how difficult it is to stretch a spring. The spring constant tells you how much force the spring exerts per unit of distance from the spring’s equilibrium state (the state where it is neither compressed nor stretched). Consequently, the spring constant can be seen as a measure of the stiffness of the spring: how much force one must exert to either stretch or compress the spring and move it from its equilibrium. The unit of the spring constant k is the newton per meter (N/m).

Let’s say that a force of 1000N extends a spring at rest by 3 meters. What is the spring constant in this situation? The spring constant can be determined by simple algebraic analysis:

1000N = -k(3m)

1000N/3m = -k

-k = 333.33 N/m

k= -333.33 N/m

That is, a spring that is stretched 3 meters by the application of a 1000N force has a spring constant value of -333.33 N/m. This value basically means that it takes 333.33 newtons to displace such a spring a distance of 1 meter. The value is negative because the force exerted by the spring is in the opposite direction than the external force stretching the spring.

The exact value of the spring constant depends on the specific spring itself. Very flexible springs would have a small spring constant and be easy to stretch or compress, while thick heavy springs would have a much higher spring constant and be harder to stretch or compress. In addition to actual springs, Hooke’s law is applicable (to an extent) in most instances where an elastic body is deformed under the application of some force: plucking a guitar string, the wind blowing and bending tall buildings, and filling up an elastic party balloon.

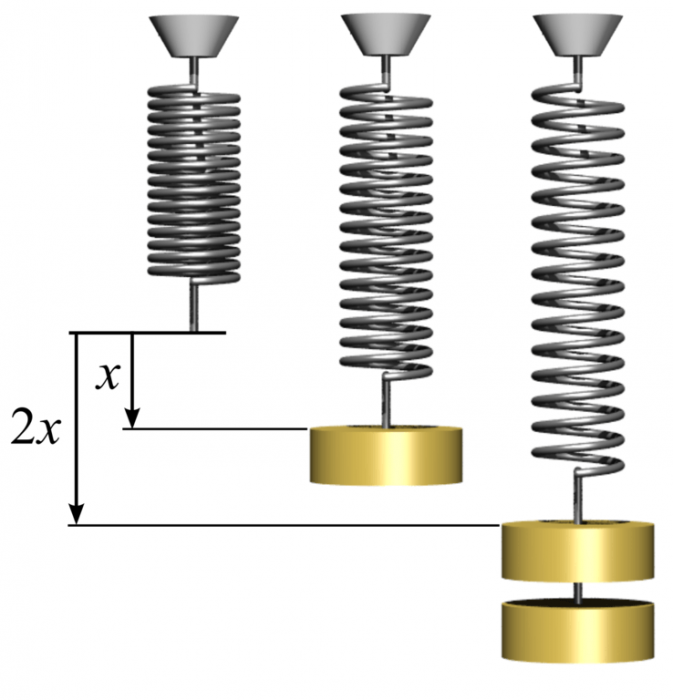
A visual representation of Hooke’s law: The extension is proportional to the force. Credit: Svjo via WikiCommons CC BY-SA 3.0

Simple Examples Of The Spring Constant In Action

Say we have a block attached to a spring-oriented horizontally and the spring is at rest. In this position, the applied force is 0 and the displacement is 0. Now say we apply some force F to compress the spring a distance of Δx, then return the spring back to equilibrium. Now let’s say we apply the same amount of force F to stretch the spring that same distance of Δx. Hooke’s law tells us that the relationship between the displacement of the spring Δx and the application of the force F during compressing and stretching can be expressed as:

|F| = k|Δx|

where k is the spring constant. In other words, the spring constant is the mathematical entity that mediates the relationship between applied force and the stretching and compressing of a spring.

Let’s put some actual numbers to the previously described scenario: Say we have a 40 cm long spring that is compressed to 35 cm under that application of a 3 N force. What is the spring constant of such a spring?

In this case our Δx is 5 cm (0.05m)) and F is 3N. Plugging these values into our equation gives us:

|3| = k|0.05|

|3|/|0.05| = k

k = 60 N/m.

That is, the spring has a spring constant k of 60 N/m. It would take 60 newtons of force to either compress or stretch the spring one meter.

Similarly, working with a given spring constant can help you predict how much a spring will stretch or compress under a given force. Let’s say we have a spring with a spring constant 87 N/m, and we tried to stretch it with a force of 212 N. How far would the spring stretch?

Once again, plugging these values into our equation gives us:

|212| = 87N/m|Δx|

|212|/87N/m = Δx

Δx = 2.43 meters

So applying a force of 212 newtons to a spring with a spring constant of 87 N/m would stretch the spring 2.43 meters.

Lastly, if we know the spring constant and the desired displacement, we can determine how much force we would need to apply to the spring to displace it that distance. Say we have a spring that we need to compress 13 cm (0.13m) and that has a known spring constant of 57 N/m. How much force would we need to accomplish this task? Plugging in the values gives us:

|F| = 57N/m|0.13|

F = 7.41 N

It would take 7.41 newtons of force to displace a spring with a spring constant of 57 N/m by a length of 13 cm.

Hooke’s Law In A Two Spring System

Say we have an object attached to two springs parallel to each other, each with a different spring constant. How are we supposed to model the combined properties of the two springs and how they affect the stretching and compression of the total system?

Luckily, there is a simple rule to describe such a system. In a system with two parallel spring each with a different spring constant, the spring constant of the total system is just the sum of the individual spring constants. That is, in a system with 2 springs and 2 spring constants k₁ and k₂, the total spring constant of that setup is just

k_total = k₁ + k₂

Systems of parallel springs can be mathematically represented as a single spring whose spring constant is the sum of the individual spring constants.

So say we have a block attached to two springs set parallel to each other, the first with a spring constant k₁=100 N/m and the second with a constant k₂=200 N/m. How much force would be required to displace the entire spring system by 5 cm?

Since we know the individual spring constants, we can just add the two values together to get the constant for the whole system. Plugging these values into our equation gives:

|F| = (k₁+k₂)(Δx)

|F| = (100 N/m + 200 N/m)(0.05m)

|F| = (300 N/m)(0.05m) = 15 N

So it would take 15 newtons of force to displace the entire spring system by 5 cm. The linear nature of the relationship between force and compression/stretching allows us to combine the properties of the two springs to model the behavior of the entire 2 spring system.

Limitations Of Hooke’s Law

Hooke’s law is a first-order approximation of the behavior of elastic materials and is not applicable in every domain. Hooke’s law only works for certain ranges of stretching/compressing, because there is a maximum distance an elastic material can be stretched or compressed before it permanently deforms. So Hooke’s law is applicable over a relatively small scale of forces. Despite this limitation, Hooke’s law is extremely useful for engineers and forms the foundation of disciplines that study spring-like phenomena, like seismology and acoustics.

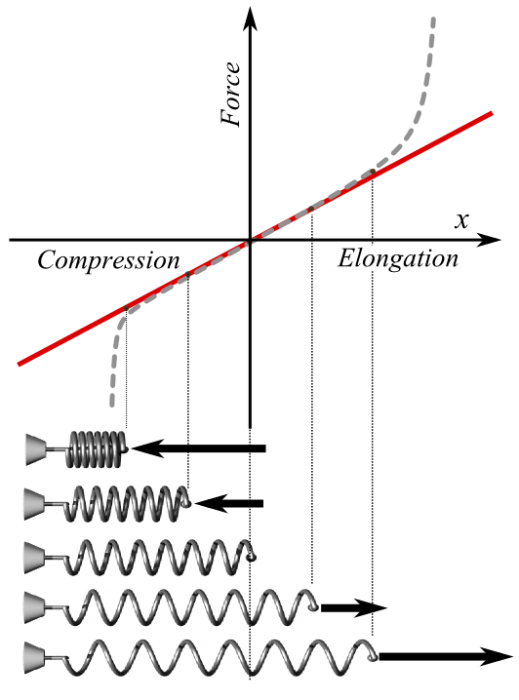
Hooke’s law is only applicable for certain degrees of stretching/compressing. Credit: “Hooke’s Law For Springs” Svjo via WikiCommons CC BY-SA 3.0.

In the more general case of the compression/stretching of elastic bodies, the mathematical form of Hooke’s law is accurate, but its specific parameters may not be. In more complex systems stresses and strains have independent components, so it would not be right to represent them with a single real number, but a tensor that maps multiple vectors to a single point in the material.

Physical Significance Of Spring Constant

These equations are all well and good, but what, exactly, does the spring constant mean in the context of physics? The other parameters of Hooke’s law, like force and displacement, clearly refer to some physical thing (force) or property (displacement), so what object or property does the spring constant refer to?

One can think of it this way: the spring constant refers to a physical property of the spring, specifically how much force the spring itself exerts in response to being compressed or stretched. According to Newton’s third law of dynamics, every action has an equal and opposite reaction. So when you pull on the spring, it pulls back with an equal amount of force. When you push on the spring, it pushes back with an equal amount of force. The spring constant is then just a measure of the relationship between this exerted force and the distance the spring moves; the amount of force exerted by the spring per unit of displacement.

Alternatively, one can think of the spring constant as a measure of how much potential energy a compressed or stretched spring has stored in its coils. Compressing or stretching a spring past its equilibrium point puts a strain on the materials of the spring, a strain that is mathematically represented as a force in the opposite direction of the push or pull. When the spring is released, that stored energy is converted into kinetic energy and the spring snaps back to its equilibrium state. Thus, Hooke’s law can be seen as a special case of the more general principles governing the relationship between kinetic and potential energy.