The Formula For Work: Physics Equation With Examples

In physics, we say that a force does work if the application of the force displaces an object in the direction of the force. In other words, work is equivalent to the application of a force over a distance. The amount of work a force does is directly proportional to how far that force moves an object. The general formula for work and for determining the amount of work that is done on an object is:

• W = F × D × cos(Θ)

where W is the amount of work, F is the vector of force,  D is the magnitude of displacement, and Θ is the angle between the vector of force and the vector of displacement. The SI unit for work is the joule (J), and its dimensions are kg•m²/s². Another way to understand it is that one joule is equivalent to the amount of energy transferred when one newton of force moves an object a distance of one meter.

Formula For Work

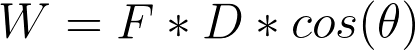
Whenever a force moves an object, we say that work has been done. When a ball rolls down a hill due to the force of gravity, when you pick up your backpack off the ground, when your car’s internal engine applies a force to make your wheels move; all of these events involve a force moving an object over a distance and so involve some work. In cases where a force is applied to an object but does not move it, no work has been done. So the force from a person pushing the side of a skyscraper is not doing any work as the skyscraper does not move. Let’s consider some simple examples to illustrate the concept of work.

Example problems

(1)

A 100 Newton force is applied to a 15kg box in the horizontal direction and moves it 5 meters horizontally. How much work was done?

In this case, we know the force is 100 N and the distance is 5 meters. We also know that since the force is applied in the same direction as the displacement, Θ is equal to 0. So we plug these values into our equation

• W = F × D × cos(Θ)

and get:

• W = 100(5)cos(0)= 500 J

So, the 100 N force did 500 joules work moving the block 5 meters.

(2)

There is a 2kg book lying on a table. A 64 N force is applied to the book at a 120° angle from horizontal and moves the book 3 meters in the horizontal direction. How much work was done?

In this case, we know the force of 64 N and the distance of 3 m. We also know that there is a 120°angle between the angle of the direction of applied force and the direction of motion. So plugging these values into our handy equation yields:

• W = 64(3)cos(120)= 156.32 Joules

So the 64 N force at a 120° angle did 156.32 joules of work moving the book 3 meters.

(3)

Linda takes a 300 N suitcase up 3 flights of stairs for a total vertical distance of 16 meters. She then pushes the suitcase with 100 N of force the remaining 8 meters to her hotel room. How much work was done over her whole trip?

This question requires 2 separate steps. There are two main portions of her trip, so we can calculate the work done over each portion individually, then, combine the two values to get the total amount of work done. For the first part of her trip, she exerts 300 N of force to move a suitcase 16 meters vertically so the amount of work done is:

• W₁=300(16)cos(0)=4800 Joules

So the first part of the trip did 4800 joules. For the second part, we know that a 100N force moved the suitcase horizontally 8 meters, so the total amount of work done on the second portion of the trip is:

• W₂=100(8)cos(0)=800 Joules

Combining the two values from each portion of the trip yields:

• W_total= W₁+W₂= 4800+800= 5600 Joules

So over the entire course of Linda’s trip, 5600 Joules of work was done.

Work/Energy Relationship

The three main equations representing the relationships between energy, work, and force.

Work and energy in physics share a close relationship. According to the work-energy principle, an increase in a rigid body’s kinetic energy is caused by an equal amount of work done on that body by a force applied to that body. In more mathematical terms, the relationship can be expressed as:

• W = KE_final−KE_initial

where KE stands for kinetic energy. In other words, the change in kinetic energy of a body is equal to the amount of work done on that body. In general, the formula for the kinetic energy of an object is:

• KE = (1/2) kg*v²

where v stands for an object’s velocity. The unit for kinetic energy is the same unit for work, the joule. Let’s look at some problems to examine these mathematical relationships.

 (4)

Donkey and Diddy Kong are sitting in a 90-kilogram minecart that is initially traveling horizontally at a velocity of 5 m/s. Rambi the rhino pushes the minecart from behind and speeds it up so it is now traveling 11 m/s. How much work did Rambi do on the minecart?

In order to solve this problem we first need to figure out the minecart’s initial kinetic energy and its final kinetic energy. Once we know those values, we can determine the total amount of work. We know both the velocity and mass of the minecart so we can determine the total kinetic energy at the beginning and at the end. The initial kinetic energy of the minecart is:

• KE_initial=(1/2)(90)(5)²= 1125 J

The final kinetic energy of the minecart is

• KE_final=(1/2)(90)(11)²=5445 J

Therefore, the total amount of work done on the minecart is 5545−1125= 4420 J.

“Science is the knowledge of consequences, and dependence of one fact upon another.” – Thomas Hobbes

(5)

A car weighing 1300 kg is moving with a velocity of 18 m/s. If 60000 joules of work is done on the car, what will its final velocity be?

The question will require a bit of algebra. First, we must determine the initial kinetic energy of the car. The initial kinetic energy of the car is:

• (1/2)(1300)(18)²=210600 J

Since we know the total amount of work done on the system (60000 J) we can figure out the car’s final kinetic energy:

• 60000=KE_final−210600
• 270600=KE_final

Now, since we know the final kinetic energy and the mass of the car, we can determine its final velocity like this

• KE_final=(1/2)kg*v²
• 270600 = (1/2)(1300)v²
• 270600 = 650v²
• 416.3 = v²
• v = 20.4 m/s

The car’s final velocity will be 20.4 m/s.

So in summation, we say work is done whenever a force moves an object over a distance. The magnitude of work is equal to the magnitude of force multiplied by the distance traveled. Work and kinetic energy are tightly intertwined and can be used to determine each other.