Weighted k-Nearest Neighbors Feature Selection (WkNN-FS)

The current digital era has brought unprecedented amounts of data. The ubiquity of various sensors, cameras, a huge amount of interaction on social networks, and the penetration of technologies into biomedicine generate terabytes of data every day. Even though methodologies in data science are advancing and are able to process real-world applications’ big data, there are still some datasets or domains where preprocessing of the data is necessary.

Before going deeper into preprocessing, let us explain how data is perceived by data scientists. The dataset can be written as a matrix consisting of rows (samples) and columns (features). The samples represent different measurements, for example, as with data taken from different patients. In this example, the columns are attributes related to one particular patient (e.g. measurements taken during a medical examination or a microarray-based gene expression profiling). Therefore, the matrix contains information about the attributes of multiple patients.

In some domains, the number of attributes is extremely high. In domains such as microarray-based gene expression profiling, this can be tens or even hundreds of thousands of attributes. The high dimensionality of data can have several negative effects on machine learning algorithms. It leads to prolonged computational times and over-fitting (reduced prediction performance due to an inability of the model to generalize). 

This problem is even more emphasized in datasets with a small number of samples. In the case of a small sample of high-dimensional datasets, some preprocessing has to be performed for machine learning algorithms to work well. The frequently employed solution is a reduction of the data dimensionality. Dimensionality reduction can be achieved through the feature selection (FS). The concept is illustrated in Fig. 1. The FS algorithm analyses the data and identifies relevant attributes.  All features evaluated as irrelevant are thrown away so the dimensionality of the dataset is significantly reduced.

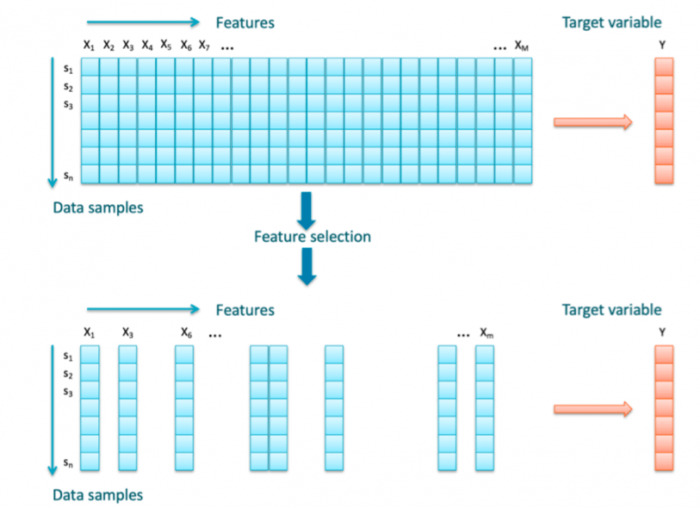
Figure 1 Feature selection. Image courtesy Peter Drotár

In a recent publication, Bugata and Drotar proposed a new FS algorithm, WkNN-FS, based on distance and attribute weighted k-nearest neighbors (KNN) with gradient descent as an iterative optimization algorithm for finding the function minima.  KNN is a supervised classification algorithm that determines the value of the target variable according to the values of the nearest data points. In conventional KNN, k nearest neighbors are all equally relevant for prediction. WkNN-FS uses distance and attributes weighted KNN, which means that the  data points closer to predicted data point are given a higher weight. Similarly, the weight of an attribute is determined according to its usefulness.

In this approach, the target variable is determined by the most relevant attributes of the most nearest neighbors. Assuming this weighting scheme, the task is to find a weighting vector that determines the importance of the features. Basically, this is an optimization task that is solved using a gradient descent algorithm. Gradient descent is an iterative optimization algorithm that utilizes the gradient of the function to find its minima. Computed weights assigned to features indicate the significance of different features.

Experimental results showed that the method is able to correctly identify significant features and boost prediction performance for high dimensional datasets. Another advantage of WkNN-FS is that its structure allows for computationally efficient TensorFlow implementation and efficient performance on GPUs. The WkNN-Fs is freely available at GITHUB https://github.com/bugatap/WkNN-FS.