Chemical sensors have gained increasing attraction for applications in environmental monitoring, industrial process monitoring, medical diagnostics, national defense, and public security. Among a variety of sensors, electrochemical sensors have a special advantage, due to high sensitivity, fast response, and long operating life. The heart of electrochemical sensor is an electrochemical transducer reporting changes in form of an electrical signal which is directly proportional to the concentration of an analyte in the solution.
A major challenge facing the construction of electrochemical sensors is to find material for an electrode with enhanced affinity for a target analyte. Discovery of graphene by Novoselov and Geim in 2004, being the first two-dimensional crystal isolated and characterized, open a route for a construction of new generation electrochemical devices. Graphene, being the material without bulk, is very sensitive to the environment which makes them a promising platform for a construction of electrochemical sensors.
Tailoring of the graphene electrode to a specific analyte is possible due to the π-electron band structure, which can be modified by crystalline lattice deformation and introducing of defects. To address the question how lattice deformation and defects impact the electron transfer kinetics between graphene and analyte, Szroeder et al. have performed simulations of the kinetics of the electrode reaction at the strained graphene electrode. In the paper, the ferri-/ferrocyanide (Fe(CN)63-/4-) ions are used as an electrochemical benchmark.
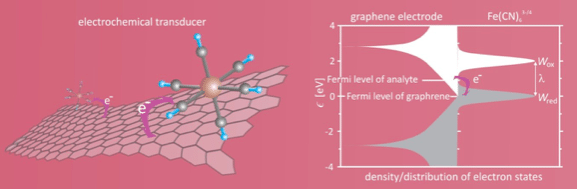
Figure 1. Electron transfer between graphene and oxidized and reduced form of analyte.
Electrode reaction rate, which is responsible for the electrical response of the transducer, depends on the electron density of states of electrode, distribution of electron states of the oxidized/reduced form of analyte, as well as the relative position of the Fermi level of the redox couple formed by the target analyte in solution with respect to the Fermi level of the electrode (graphene). For the perfect freestanding graphene, the density of states near the Fermi level decline linearly with decreasing absolute energy with respect to the Fermi level and reaches the value zero at the Fermi level. Due to the confined dimensionality, a pair of the van Hove singularities appears at energy ±2.78 eV.
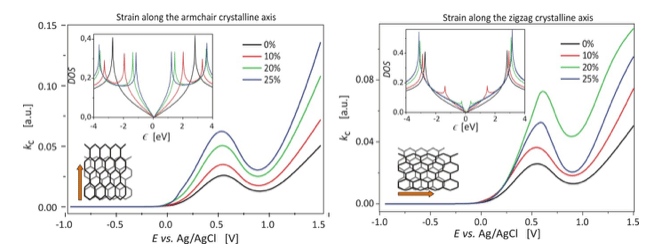
Figure 2. Reaction rate of the reduction of the Fe(CN)63- ions at the strained graphene electrode.
The simulated curve of the cathodic reaction rate for reduction of the Fe(CN)63- ions is not a monotonically increasing function of the electrode potential. Due to the zero density of states near the Fermi level, the valley is observed above the local maximum.
When the graphene electrode is stretched along the armchair crystalline axis, the slope of the electron density of states increases and an extra pair of singularities appears. The singularities shift towards the Fermi level with increasing strain. Stretching along the zigzag axis boosts the reaction rate – the hump in the curve of cathodic reaction rate is growing with increasing strain.
Stretching along the zigzag crystalline direction produces slightly different effects. The density of states spectrum loses its linear dependence near the Fermi level. The van Hove like singularities appear, as in a case of the armchair strain, but they shift faster into the Fermi level with increasing strain. Higher strain induces the band gap opening. The moderate zigzag strain facilitates the electrode reaction rate much better than the armchair strain. The hump in the curve of the cathodic reaction rate builds up faster than under the armchair strain. However, at higher values of strain (> 20%), electrode reaction rate declines due to the band gap.
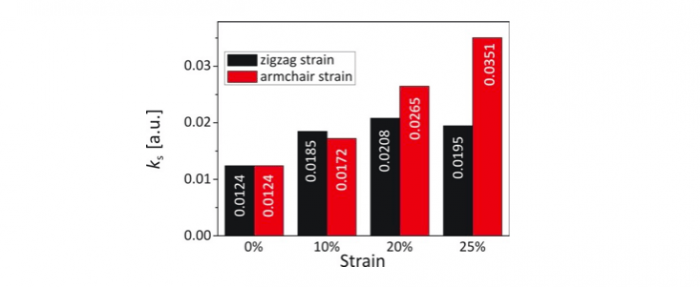
Figure 3. Standard electron transfer rate constant for the ferri-/ferrocyanide redox couple at the strained graphene electrode
A parameter that characterizes the kinetics of electrode reaction for a specific pair of ions is the standard electron transfer rate constant. Calculated values of the constant for the ferri-/ferrocyanide redox couple values show that the strain applied along the armchair direction causes a monotonic increase of the standard rate constant up to the strain of 25%, which is the failure strain of graphene. The electrode reaction proceeds three times faster at graphene electrode stretched along armchair by 25%. However, for moderate strain (< 20%), deformation along the zigzag direction is more efficient and causes a faster increase in the standard rate constant. Reaction kinetics increases by half at the zigzag strain of 10%. Under higher strain, band gap hinders a fast growth of the standard rate constant.
Introduction of charged adatoms (alkali and the group III metals) or substitutional impurities such as N atoms into the strained graphene lattice in a concentration of 0.1% gives rather poor results. The electrode reaction rate increases, respectively, by 2.2% and 3.4%. Covalently bonded moieties and vacancies do not facilitate electrochemical performance of the stretched graphene.
These findings are described in the article entitled Effect of uniaxial stress on the electrochemical properties of graphene with point defects, recently published in the journal Applied Surface Science. This work was conducted by Pawel Szroeder from Kazimierz Wielki University, Igor Sagalianov and Yuriy Prylutskyy from Taras Shevchenko National University of Kyiv, Taras Radchenko and Valentyn Tatarenko from Kurdyumov Institute for Metal Physics in Kyiv, and Wlodek Strupinski from Warsaw University of Technology.
Figures 2 and 3 are reprinted from Applied Surface Science, Vol 442, P. Szroeder, I. Sagalianov, T. Radchencko et al., Effect of uniaxial stress on the electrochemical properties of graphene with point defects, Pages No. 185-188, Copyright (2018), with permission from Elsevier