
Incompressible fluids are fluids that do not change their volume while they flow. Water in the oceans and air in the atmosphere are examples of incompressible fluids. The equations of motion for a viscous incompressible fluid are the Navier-Stokes equations (NSE). In 1822 Claude Louis Marie Navier, a French mathematician-engineer, derived the NSE.
Afterwards, in 1845 George Gabriel Stokes, a British mathematician-physicist, published a derivation of the NSE in a manner that is followed in most current texts today, making it clear that the parameter appearing in the equations has an important physical meaning: it measures the magnitude of the viscosity (the friction of the fluid)—whence comes out the name Navier-Stokes equations.
The lid-driven square cavity is a problem of the classic fluid mechanics where the domain is the unit square cavity and the viscous incompressible fluid therein is governed by the NSE. From the dynamical systems theory stems that all solutions to this problem converge to a global attractor, an ensemble with many mathematical properties.
Notwithstanding, the theory indicates that all solutions to this problem stand close to the global attractor after a time long enough and gives no indication at all about this time neither about the look of the global attractor.

Fig. 1 displays the phase diagram at Re=5,000 at the point (7/8,1/8).
Henceforth, let us follow the path of the modeling cycle to obtain more information about this strange ensemble. The continuous model is known: the NSE. Then it has to be set up the discrete model and the simulation.
A combination of known methods is used to discretize and solve the NSE: the linear Linθ∗-scheme, the projection method, the Conjugate Gradient method, the Bi-CGSTAB method, the Fast Fourier Transform method—and the incremental unknowns method as a spatial preconditioner. The linear Linθ∗-scheme is used for the temporal discretization—∆t is the time step— and a staggered marker-and-cell (MAC) mesh with finite-differences is used for the spatial discretization—h is the spatial mesh size. The matrix structure of every underlying linear system is detailed along the papers therein.
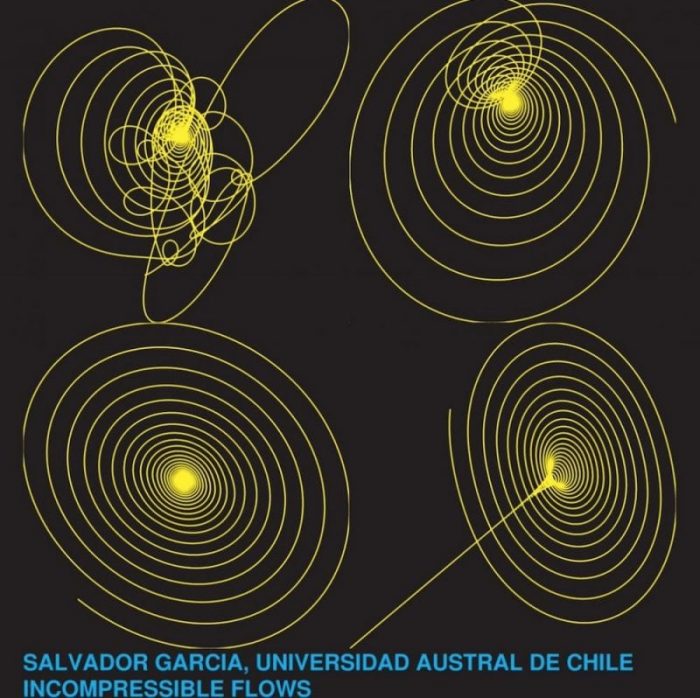
Fig. 2 displays the detailed phase diagram at Re=5,000 at the point (7/8,1/8).
The combination of known methods before produces a Direct Numerical Simulation (DNS) which simulates the flow. It runs in double precision from t = 0 to a sufficiently long time t∞ = 50, 000. The spatial mesh size h = 1/256 is used throughout. And the time step ∆t = 2h, h. As many as needed DNSs are produced and then direct observations of them are at the core of the temporal limit’s study.
As the Reynolds number (a dimensionless parameter related to the reciprocal of the viscosity) Re → ∞, the temporal limit (at the Reynolds number Re fixed and as the time t → ∞) of the lid-driven unit square cavity flow evolves from stationary to periodic to aperiodic and then to chaotic. The primary eddy switches from clockwise- to counterclockwise-rotating. The primary eddy is the eddy leading the dynamics. Four principles appear at the genesis of small counterclockwise- or clockwise-rotating eddies.

Fig. 3 displays the stationary temporal limit at Re=5,000.
In the end, at extreme Reynolds numbers, the adjacent counterclockwise- rotating eddies coalesce into a wide, prevailing counterclockwise-rotating eddy in the square cavity’s central region—the actual primary eddy. The adjacent clockwise-rotating eddies circulating counterclockwise around it are unable to coalesce and to break it up. It seems that the eddies of each kind coalesce to attain the maximum extension available. But there is not enough room in the unit square cavity for a wide eddy of each kind to stand up as the fluid evolves.
Notwithstanding, it is not certain that the dynamics observed at high and extreme Reynolds numbers represents indeed true physics. But yet, it appears to agree with the theory where wide eddies of each kind form out as the fluid evolves.
The paper Chaos in the lid-driven square cavity, Volume 142, December 2017, Pages 98–112 appeared in Mathematics and Computers in Simulation. It is the last of 6 papers of the same author on the lid-driven square cavity flow, finishing his research on this subject. For the last 4 papers the computations have been carried out—almost alone, day and night—at the cluster in The Institute for Scientific Computing and Applied Mathematics on the Bloomington Campus of Indiana University for 10+ years through the internet from the Instituto de Ciencias Fisicas y Matematicas on the Campus Isla Teja of the Universidad Austral de Chile.
The study, Chaos in the lid-driven square cavity was recently published in the journal Mathematics and Computers in Simulation.








