On Dynamics Of Sine-gordon Soliton Under External Forcing

Solitons are pulsed like waves that propagate and collide with each other without losing their speed, shape or amplitude. This was first observed by John Scott Russel in a water canal near Edinburgh in 1834. Since then they have been found in several other fields like optical fibers, superconductor devices and galaxies from scales ranging from 10−9 m to 109 m. Soliton wave emerges in various physical applications like defects in solids, shallow water waves,

Josephson junction oscillator, relativistic field theory, earthquakes, mechanical transmission lines etc. A mathematical model in the form of a nonlinear partial differential equation whose solutions exhibit soliton behavior was first introduced in 1877 by the French mathematician Joseph Valentin Boussinesq and later rediscovered in 1895 by the Dutch mathematicians Diederik Korteweg and Gustav de Vries. This equation is nowadays known as the KdV equation.

The particle-like behavior of solitons inspired the British physicist Tony Skyrme to suggest in 1961 that spatially localized solutions to nonlinear partial differential equations describing waves can be considered as particles. This idea was demonstrated by Skyrme for the sine-Gordon (sG) equation. The sG equation was originally introduced in 1862 by Edmond Bour in the course of study of surfaces of constant negative curvature as the Gauss-Codazzi equation in R3. This was rediscovered in 1939 by Frenkel and Kontorova in their study of crystal dislocations.

This equation attracted a lot of attention in the 1970s due to the presence of soliton solutions. It was found that two colliding solitons interacted in a manner that was very similar to two solid particles colliding with each other. It was then thought that solitons would also behave like Newtonian particles under the influence of a constant force. A constant force in Newton’s equation would mean a quadratic function in time t simply because a function whose second derivative is constant means that the function is quadratic. The theme of the early 1980’s was to see if solitons too accelerate quadratically with respect to time if a constant force was introduced in the sG equation.

In 1981 Fernandez et al. found that the acceleration of the sG solitons by a constant force increases as t2 only for small times whereas for larger times it behaves like tanh t. Proceeding with the same theme Reinisch & Fernandez studied a soliton kink solution and found that they too do not behave like a Newtonian particle. Summarizing these studies Kaup in 1984 argued that soliton or kink is not a rigid point particle and it needs to be qualified up to what extent one is referring to a “Newtonian” or a “Non-Newtonian” particle. In 2017 Jagtap et al studied the sG equation with F replaced by

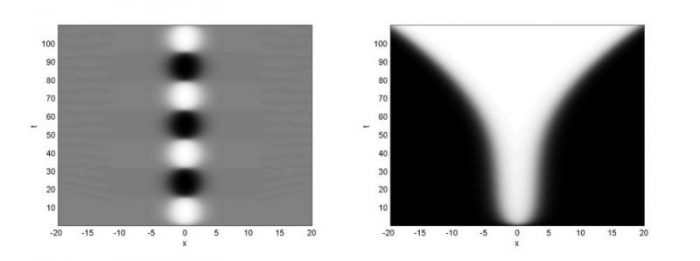
Figure 2: Breather solutions for homogeneous (left column) and inhomogeneous sG equations (right column). Republished with permission from Elsevier from https://doi.org/10.1016/j.wavemoti.2017.05.003

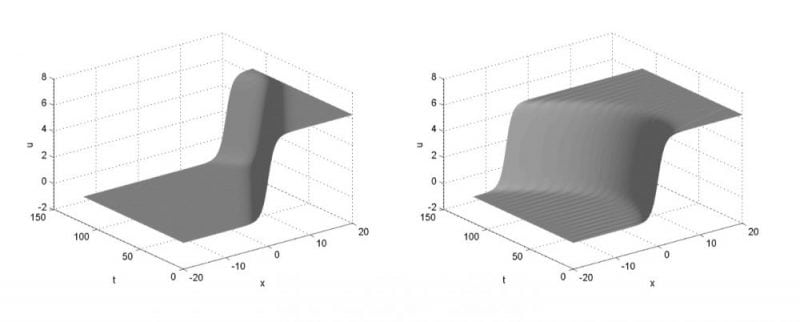
AH(x − t) where A is constant and H(·) is the Heaviside function. Numerical experiments are performed on kink and breather test cases. Figure 1 shows the kink solution for homogeneous sG equation (left) and for inhomogeneous sG equation with Heaviside forcing (A = 0.007) on right. In this study, it is found that at a critical value of A even soliton behavior of kink breaks down which supports the theory that, soliton does not behave like Newtonian particles under the influence of a constant force.

Similarly, for breather test case shown in figure 2 with homogeneous sG breather solution (left) and inhomogeneous sG equation with Heaviside forcing on he right where the value of A = 0.0076 is the critical value at which breather solution is completely destroyed. For more details, we refer to our paper in Wave Motion.

References

1. Jagtap A.D., Saha E., George J.D. and Vasudeva Murthy A.S., Revisiting the Inhomogeneously Driven sine-Gordon Equation, Wave Motion (73) 76-85, 2017.
2. Jean-Claude Fernandez, et al., Sine Gordon Solitons Do Not Behave Like Newtonian Particles, Physical Review Letters, Vol.46, No.12,1981.
3. Kaup D.J., Comment on Specific sine-Gordon soliton dynamics in the presence of external driving force, Phys. Rev. B, Vol 29, No. 2, 1071, 1984.
4. McLachlan, R., A gallery of constant-negative-curvature surfaces, Math. Intelligencer 16 (1994), no. 4, 31-37.
5. Reinisch G., Fernandez J.C., Specific sine-Gordon soliton dynamics in the presence of external driving forces, Phys. Rev. B, Vol. 24, 835, 1981.
6. H.R., Particle States of Quantized Meson Field, Proc. R. Soc. Lond. A1961, 262, 237-245.

The study, Revisiting the inhomogeneously driven sine–Gordon equation was recently published by Ameya D. Jagtap, Esha Saha, A.S. Vasudeva Murthy from the Centre for Applicable Mathematics (TIFR-CAM), Bangalore in the journal Wave Motion.