
In geometry, a rhombus is a special kind of quadrilateral in which all 4 sides are of equal length. A rhombus has certain unique properties that are a consequence of its definition. Some key properties of a rhombus include:
- Opposite angle are congruent
- Adjacent angles are supplementary
- Diagonals bisect opposite angles
- Diagonals bisect each other
- Diagonals are perpendicular to each other
Definition Of A Rhombus
At its simplest, a rhombus is defined as any simple (non-intersecting) quadrilateral that has 4 sides equal in length. According to this definition, a square is also a rhombus, one in which all of its angles are right angles. Other names for a rhombus include “equilateral quadrilateral” and “lozenge”, though the latter term is normally reserved for the special rhombus that has 2 45° angles and 2 135° angles.
It can be proven that the rhombus is a special case of the parallelogram, one in which all 4 sides are equal length. This means that all rhombi are parallelograms, though the opposite does not necessarily hold as there are parallelograms that are not rhombi. Every rhombus is a kite—a quadrilateral with congruent adjacent sides.
The word “rhombus” comes from an ancient Greek word meaning “to spin.” Euclid used the term “rhombus” to describe that 2-D shape that arises from taking the cross section of two circular cones that adjoin at the base.
Essential Properties of A Rhombus
1. Opposite Angles Are Congruent
The first key property of a rhombus is the relationship shared between pairs of opposite angles. Pair of opposite angles in a rhombus are congruent, meaning that they are of equal measure. We can prove this with the following:
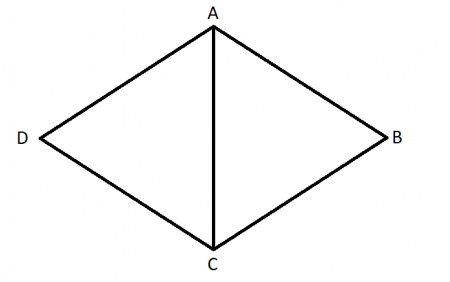
Credit: Author
| Statement | Reason | ||
| 1 | Rhombus ABCD | 1 | Given |
| 2 | Draw line AC | 2 | 2 points make a line |
| 3 | AB||DC & BC||DA | 3 | Def. of Rhombus |
| 4 | ∠ACD ≅ ∠BAC & ∠DAC ≅ ∠ACB | 4 | Alternate interior angles |
| 5 | AB = BC = CD = DA | 5 | Def. of a rhombus |
| 6 | ΔACD = ΔABC | 6 | SAS |
| 7 | ∠D ≅ ∠B | 7 | CPCTC. Q.E.D |
This property of a rhombus also shows that is is a parallelogram as an essential property of a parallelogram is that its opposite angles are congruent. That is if a quadrilateral has congruent opposite angles, that is enough to guarantee it is a parallelogram.
(Sidenote: “Q.E.D” at the end of each proof is an abbreviation for the Latin phrase “quod erat demonstradum” which roughly translates to “thus it has been demonstrated.”)
2. Adjacent Angle Are Supplementary
Adjacent angles of a rhombus are supplementary, meaning that they add up to 180°. We can prove that adjacent angles in a rhombus are supplementary by the following:

Credit: Author
| Statement | Reason | ||
| 1 | Rhombus ABCD | 1 | Given |
| 2 | AB || DC & DA || BC | 2 | Def. of a rhombus |
| 3 | AC | 3 | Two points make a line |
| 4 | ∠A supp ∠B, ∠B supp C, ∠C supp ∠D, ∠D supp ∠A | 4 | It two || lines are cut by a trans., interior angles on the same side of the trans. are supplementary. Q.E.D |
So we can prove that adjacent angles in a rhombus are supplementary.
3. Diagonals Bisect Opposite Angles
The third major property of a rhombus has to do with its diagonals. A diagonal of a polygon is any line that is drawn between two non-adjacent vertices. A parallelogram has 4 points, meaning it has a total of 2 diagonals. A characteristic property of the diagonals of a rhombus is that they bisect the angle they are drawn from. We can prove this with the following:

| Statement | Reason | ||
| 1 | Rhombus ABCD | 1 | Given |
| 2 | AB = BC = CD = DA | 2 | Def of a rhombus |
| 3 | AC & BD | 3 | Two points make a line |
| 4 | AC = AC | 4 | Reflexive property |
| 5 | ΔABC = ΔADC | 5 | SSS |
| 6 | ∠BAC = ∠ACB
∠DAC = ∠ACD |
6 | Base ∠s of isos. triangles are congruent |
| 7 | ∠DAC = ∠BAC
∠DCA = ∠BCA |
7 | CPCTC |
| 8 | AC bisects ∠DAB
BC bisects ∠ADC |
8 | An angle bisector divides an angle into two equal parts. Q.E.D |
So we have just proven that the diagonals of a rhombus bisect the opposite angles. This is a unique property of rhombi that is not seen in other kinds of quadrilaterals.
4. Diagonals Bisect Each Other
The 4th major property of a rhombus also has to do with its diagonals. It is a fact that for a rhombus its diagonals bisect each other; that is, they each cut each other into two equal line segments. The point at which they intersect is the middle of both diagonals.

| Statement | Reason | ||
| 1 | Rhombus ABCD | 1 | Given |
| 2 | AB = BC = CD = DA | 2 | Def. of a rhombus |
| 3 | AB || CD & DA || CB | 3 | Def. of a rhombus |
| 4 | ∠AEB = ∠DEC | 4 | Pairs of vertical angles |
| 5 | ∠BAC = ∠ACD | 5 | Alternate interior angles |
| 6 | ΔAEB ≅ ΔDEC | 6 | SAA theorem |
| 7 | AE = EC
DE = EB |
7 | CPCTC |
| 8 | AC and DB bisect each other | 8 | Two lines bisect each other if the point at which they intersect is the midpoint of both lines. Q.E.D |
5. Diagonals Are Perpendicular To Each Other
The last defining feature of a rhombus that we will prove is the fact that is diagonal lines are perpendicular to each other. In a rhombus, the two diagonals always intersect at a right 90° angle. We can prove this as folows:

| Statement | Reason | ||
| 1 | Rhombus ABCD | 1 | Given |
| 2 | AB = BC = CD = DA | 2 | Def. of a rhombus |
| 3 | AE = EC
DE = EB |
3 | Theorem: diagonals of a rhombus bisect each other (from proof #4) |
| 4 | ΔAEB = ΔBEC = ΔCED = ΔAED | 4 | SSS |
| 5 | ∠AEB = ∠BEC = ∠CED = ∠DEA | 5 | CPCTC |
| 6 | ∠AEB + ∠BEC + ∠CED + ∠DEA = 360° | 6 | Sum of angles surrounding a point and sharing a vertex is 360° |
| 7 | 4∠AEB = 360° | 7 | Simplification |
| 8 | ∠AEB = 90° | 8 | Division |
| 9 | AC ⊥ BD | 9 | Two lines are perpendicular if they intersect at a right angle |
Other Properties Of A Rhombus
Area
The area of a rhombus can be calculated exactly the same as every other kind of quadrilateral, multiply the base times the height.
A = b x h
The height of the rhombus is the measure of a line drawn a perpendicular from one side to the opposite side. The reason why the area formula for a rhombus is the same as a rectangle is simple; every rhombus (and parallelogram) can be cut into pieces and rearranged into a rectangle with the same base and height (the following picture is of a non-rhombus parallelogram, but the same principle holds for rhombi).
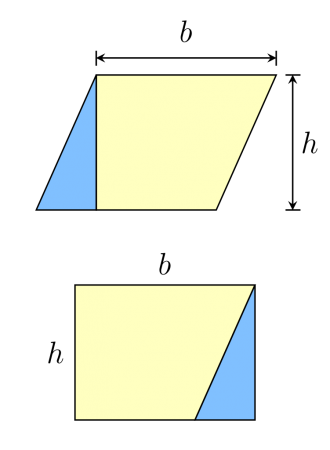
Credit: WikiCommons CC0 1.0
If you draw a line perpendicular from one base to the end of another base, you get a trapezoid and a right triangle that you can rearrange into a rectangle with the same area as the original rhombus.
You can also compute the area of a rhombus if you only know the length of its diagonals. The area of a rhombus is equal to half the product of its diagonals. So for a rhombus with diagonals p and q, the mathematical formula is:
A = pq/2
Remember that we previously proved two things about the diagonals of a rhombus: they bisect each other and they are perpendicular to each other. Consider the following rhombus:

We know that AE = EC and DE = EB. We also know that the diagonals bisect the pairs of opposite angles. So we get two big isosceles triangles on the right and left, each divided into two smaller right triangles. The area of the entire rhombus is equal to two times the area of one of the isosceles triangles. Starting with the right one ΔABC, we know that its total area is
Area ΔABC = ½(AC)(EB)
However, we also know that EB is half of DB (because the line is bisected at point E) so we can substitute:
Area ΔABC = ½(AC)(½DB)
which simplifies to
Area ΔABC = ¼(AC)(DB)
Since we know the entire area of the rhombus is twice the area of ΔABC, we can rewrite
Area ABCD = 2 × Area ΔABC = ½(AC)(BD)
Therefore, the area of a rhombus can be calculated as half the product of its diagonal lines.
Tessellation Properties
The rhombus can also form tessellation, meaning you can arrange rhombus in regular patterns to completely fill a 2-dimensional face. A tessellation made out of rhombi is called a rhombille tiling. Tilings of identical rhombi can fill a plane in three different ways; as a consistent stack of diamond, an alternating stack of diamonds, or as groups of 3 rhombi arranged in a cube face.

One of the three possible periodic rhombille tilings. Credit: Public Domain
You can also form the rhombille tiling from a regular tiling of hexagons. Simply divide each hexagon into three by drawing lines from every other vertice that meet in the center of the hexagon.
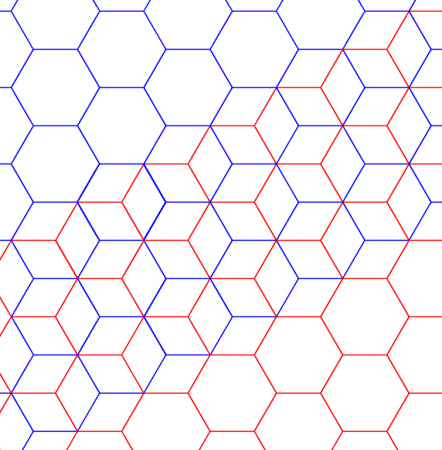
You can form a rhombille tiling from a hexagonal tiling. Credit: WikiCommons CC BY-SA 3.0
Rhombi can be arranged into tessellation because they can be arranged in such a way that the sum of angle surrounding each point is exactly 360 degrees. This is a necessary property of shapes that can be tessellated; if you can’t arrange a shape in such a way that the sum of all the angles that meet at a vertex is 360, then you cannot make a regular tessellation out of it.
To sum up, a rhombus is the name of a quadrilateral in which all 4 sides are of equal length. All rhombi are parallelograms and a square is a special case of a rhombus in which all 4 interior angles are right angles. The key properties of a rhombus are its opposite angles are congruent, its adjacent angles are supplementary, its diagonals bisect opposite angles, its diagonals bisect each other, and its diagonals are perpendicular to each other.








