
The classical equation for force is one of the most important equations in physics. The force equation is a simple formula that captures the relation between the physical quantities of force, mass, and acceleration, and how changes in these quantities cause changes in the others. Mathematically, the force equation is:
F = m × a
Where F stands for force and m and a stand for mass and acceleration, respectively. The force equation is a mathematical encapsulation of Newton’s second law of motion, which can be stated as:
Newton’s second law: the acceleration of an object due to an impressed force is directly proportional to the magnitude of the force, in the same direction as the force, and inversely proportional to the mass of the object.
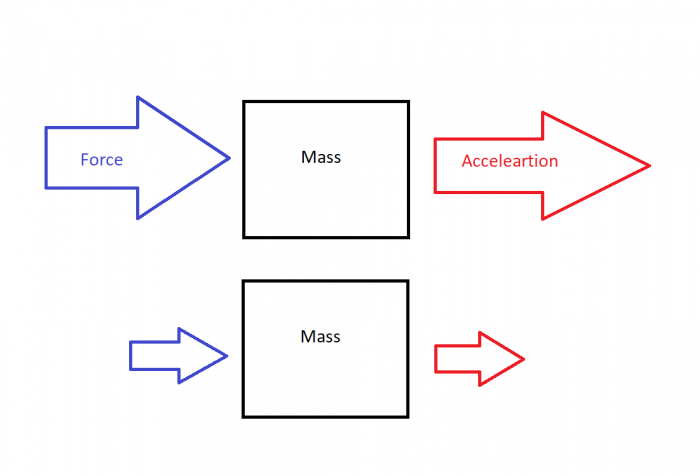
An illustration showing Newton’s second law. the amount of acceleration is directly proportional to the amount of applied force. The more force, the more acceleration; the less force, the less acceleration. Credit: Author
Essentially, the force equation tells that in the face of a constant force, a more massive object will be accelerated slower than a less massive object. Conversely, the greater the applied force is, the greater an object accelerates. The force equation gives us a way to determine the magnitude and direction of a force acting on an object by measuring its mass and acceleration. It also gives us a way to predict how some object will move when acted upon by a force.
Let’s take a step back and look at each parameter of the force equation (mass, acceleration, and force) to see how they all fit together to describe and explain motion.
Mass

Credit: Pixabay CC0 1.0
In a nutshell, the mass of an object is a measure of how much “stuff” makes up an object. The more “stuff” an object contains, the more massive it will be. The mass of an object determines how resistant it is to changes in its state of motion. This understanding of mass in intuitively obvious: a very massive object requires a lot of effort to move. The mass of an object also determines the strength of the gravitational attraction it exerts on other objects. The SI unit for mass is the kilogram (kg).
Acceleration

Acceleration is change in velocity over time. Credit: Public Domain
The acceleration of a body refers to the rate of change in the velocity of an object over some amount of time. Acceleration is a vector quantity, meaning that it has two parts: a magnitude and a direction. The magnitude of acceleration is the amount by which the object’s velocity is changing per unit of time. The direction of acceleration determines which direction the object accelerates in. For example, if a car starts from a standstill and speeds up, it is accelerating in the direction of motion. If a moving car begins to slow down, it is accelerating in the direction opposite the direction of motion (decelerating).
The SI unit for acceleration is the meters per second per second, often written as m/s2. The “second per second” part indicates that the velocity (meters per second) is changing by some amount for every second.
Force
A force, understood in its broadest sense, is any interaction that can cause a change in an object’s state of motion. Intuitively, forces can be conceptualized as things that “push” or “pull” objects around. Force, like acceleration, is a vector quantity and so has both a magnitude and direction. The magnitude and direction of acceleration of an object are dependent on the vector sum of the individual forces acting on the object. The SI unit for force is the Newton (N) where 1 N is defined as the amount of force required to accelerate a 1 kg object by 1 m/s2. So, if we had a one-kilogram block, a force of 1 N would cause that block to accelerate by 1 meter per second per second.
Forces are extremely important in classical physics because they explain how objects change their state of motion. According to Newton’s first law of motion, an object in a constant state of motion will continue in that state of motion indefinitely, unless acted upon by an external force. This is a crucial point that confuses many physics students. An object does not require any force to sustain its state of motion. Rather, objects require forces to change their state of motion. This is precisely the opposite view of Aristotelian theories of motion, according to which constant motion required the constant input of a force.
Thus, forces are described mathematically in terms of how they change an object’s state of motion. For an object of a constant mass, a larger force will result in greater acceleration and a smaller force a smaller acceleration. The classic example of a force is gravity. Gravity is a force because it causes a change in the state of motion of objects.
Overview Of The Force Equation
To reiterate, the force equation is:
F = m × a
Here is a table that charts the force, mass, and acceleration of some hypothetical bodies:
| Force (N) | Mass (kg) | Acceleration (m/s2) |
| 10 | 2 | 5 |
| 20 | 2 | 10 |
| 20 | 4 | 5 |
| 10 | 2 | 5 |
| 10 | 1 | 10 |
Simply looking at this table of numbers should make apparent some qualitative relationships between force, acceleration, and mass. For instance, comparing values in rows 1 and 2 shows that, for a constant mass, doubling the force results in a doubling of acceleration. Conversely, by looking at rows 2 and 4, we can see that halving the force results in halving acceleration. Extrapolating this trend, we see that tripling the force triples the acceleration, and so on. Acceleration is directly proportional to force.
Likewise, we can see a qualitative relationship between mass and acceleration. Looking at rows 2 and 3 shows us that, for a constant force, doubling the mass results in halving the acceleration. From rows 4 and 5, we can see that halving the mass doubles the acceleration. Acceleration is inversely proportional to mass.
Sample Problems
Let’s tackle some sample problems to put some explicit numbers to these abstract formulae.
Q1.) A 5 kg block is acted upon by a 42 N force. What is the acceleration of the block?
Q2.) A 62 N force is impressed on an object and causes it to accelerate at 15 m/s2. What is the mass of the object?
Q3.) Suppose an object is accelerating at a rate of 2 m/s2. If we triple the force and double the mass, then what is the new acceleration of the object?
Q4.) What is the magnitude of the force acting on a body that is traveling at a constant velocity of 8 m/s?
Q5.) The acceleration from gravity on Earth is 9.8 m/s2. On the moon it is 1.6 m/s2. For a 50 kg person, what is the difference in the magnitude of the force acting on them on the surface of the moon compared to the surface of the Earth?
Answers
Q1.) This one is simple. All we have to do is plug in our values into the force equation and compute the answer:
42 = 5kg(a)
42/5 = a
a = 8.4 m/s2
So a 5 kg block will accelerate by 8.4 m/s2 when a 42 N force is applied.
Q2.) Once again, plugging in the values and doing some algebra will give us the right answer:
62 = m(15m/s2)
62/15 = m
m = 4.13 kg
So the mas of a body that is accelerated by 15 m/s2 under the application of a 62 N force is 4.13 kg.
Q3.) For this problem, we need to recall the qualitative relationships that hold between force, mass, and acceleration. Remember that tripling the force triples the acceleration and doubling the mass halves the acceleration. This means that to find the new acceleraiton, we multiply the old acceleration by a factor of 3 then by a factor of ½. Together, this is the same as multiplying the acceleration by a factor of 3/2. Thus:
a2 = a1 (3/2)
a2 = 2(3/2)
a2 = 3 m/s2
So the new acceleration of the object would be 3 m/s2
Q4.) Think carefully about this one. What does it mean to say a force is acting on a body? It means that the body is accelerating in some way. How much acceleration does a body moving at a constant velocity undergo? The answer is 0 N. If an object is moving at a constant velocity, it is not accelerating, and therefore there is no force acting on it or, more specifically, there is no net force acting on it. There could be multiple individual forces acting on the object but the vectors can align in such a way that they completely cancel each other out. So the total magnitude of the force acting on an object moving at a constant velocity of 8 m/s is 0 N.
Q5.) This question requires two steps. First, we need to find the force acting on a 50 kg person on the surface of the Earth and the force acting on that same person on the surface of the moon. Then we need to find the difference between the two magnitudes.
NE = 50kg(9.8m/s2) = 490 N
NM = 50kg(1.6m/s2) = 80 N
490 N − 80 N = 410 N
So the difference in the magnitude of the force is 410 N.
Key Points To Take Away
- F = m×a
- Newton’s second law state that force and acceleration are proportional
- Consequently, acceleration is inversely proportional to mass
- For a constant mass, a greater force will cause a greater acceleration








