Structuring Data Sets By Defining Topological Relations: The Example Of Word Morph

Some years ago we got a request by language therapists if we could construct a computer program for patients with difficulties of word finding. The therapists had already successfully used the well-known language game “Word Morph” to increase the language abilities of their patients.

Word Morph is a game similar to “Scrabble”: Its basic rule is simply to construct new words by exchanging one letter in a “start word” and thus to generate a word chain until an also predetermined “end word” has been found. The words must, of course, consist of the same number of letters. An example of such a word chain is “break – bread – tread – trend”.

An Algorithmic Solution

In order to solve this problem, we defined a word set as a “metrical space”, i.e. a set where between two words X and Y a distance relation d(X,Y) = n can be constructed; n is – in this case! – an integer. For the problem of Word Morph, we defined d(X,Y) = 1 if and only if X and Y differ in exactly one letter. For example d(break, bread) = 1. In terms of metrical topology all words Y with d(X,Y) = 1 define a so-called sphere neighborhood of X with radius r =1; “bread” hence belongs to the sphere neighborhood of “break” and “trend” to the neighborhood of “tread”.

The algorithm to construct word chains in a given word set now operates the following way: It starts from the predetermined start word X and generates the sphere neighborhood of X, i.e. it selects all words Y with d(X,Y) = 1. We call this the first order neighborhood of X. If the end word Z belongs to this first order neighborhood the algorithm stops. If Z is not an element then the algorithms constructs the neighborhoods of the words Y, i.e. set of words S with d(S, Y) = 1 and d(X,S) = 2. This generates the second order neighborhoods with respect to X. This procedure is repeated until Z has been found as an element of an n^th order neighborhood of X. This gives the distance d(X,Z) = n. Because the task of the algorithm is the generating of neighborhoods we call it ANG – Algorithm for Neighborhood Generating.

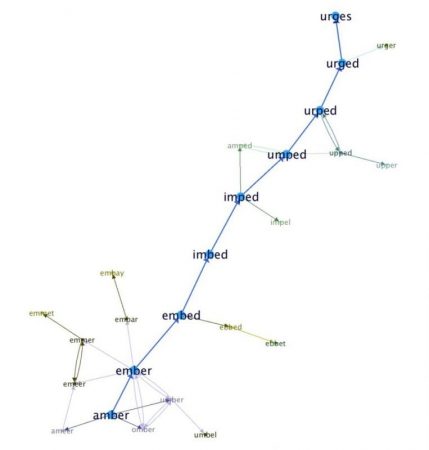
Picture 1 shows a graph starting with “amber” and ending with “urges”

In large word sets, it might quite be that Z cannot be reached that way. This means that the whole word set is not connected. In this case, after having constructed all possible neighborhoods ANG selects at random a word from the remaining subsets and repeats its operations. The result is a partition of the initial word set, i.e. a decomposition of the set into disjoint subsets.

In addition to the original Word Morph rule, we not only experimented with r = 2 but also introduced the possibility to construct “vertical” neighborhoods, namely adding (or subtracting) one letter. By calling the first neighborhoods “horizontal” ones we obtain for example “push” as an element of the horizontal neighborhood of “bush” and “brush” as an element of the vertical neighborhood of bush. Details and results of experimenting with these enlargements of Word Morph can be found in Klüver et al 2016.

Final Remarks

Apart from the rather serious problems the language therapists told us the dealing with Word Morph might look on a first sight as an example of a “Glass Bead Game”, to quote the famous novel of Herrmann Hesse. Yet we could show that ANG can be applied to very different practically important problems, for example, a) the selection of suited locations for offshore wind energy plants, b) the structuring of social groups, c) the construction of an Internet metasearch engine that computes the information degree of text documents, d) the ordering of medical data and e) the ordering of log files.

The basic logic is always the same, namely the definition of a metrical distance relation between two elements of a data set and the subsequent generation of according neighborhood structures. Therefore, the construction of ANG for Word Morph might be seen as a classic case of “Serendipity”: We got much more than originally intended.

References

• Klüver, J., Klüver, C. Ordering data sets by generating graph structures. In: Brito, A.C., Tavares, J.M.R.S., De Olivera, C.B. (Eds): Proceedings of the 2014 European Simulation and Modelling Conference (ESM ‘2014). Eurosis-ETI, 2014, 97 – 102
• Klüver, J., Schmidt, J., Klüver, C., 2016: Word Morph and Topological Structures: A graph generating algorithm. In: Complexity Vol. 21, Issue S1, pp. 426 – 436. DOI:10.1002/cplx.21756

This article, with contributions from Christina Klüver and Jürgen Klüver titled Word morph and topological structures: A graph generating algorithm was recently published in the journal Complexity.