Sintering And Densification In Nuclear Power

Like most power plants, nuclear power plants heat water to generate electricity. But nuclear power plants use heat from splitting atoms rather than burning fossil fuels. Thus, they provide energy without significant carbon emissions. However, nuclear power is facing economic challenges due to ever-stricter and more expensive safety requirements and cheap natural gas. This means costs need to go down in order to compete.

Therefore, the nuclear industry needs to constantly improve safety while reducing cost. One way to do this is by improving the manufacturing processes used to make the uranium dioxide (UO₂) pellets that fuel our existing reactors. Computer models could play a critical role in designing the fuel to be both safer and less expensive. A recent review article in the Journal of Nuclear Materials summarizes how the fuel pellets are manufactured, how this process has been modeled, and where improvements are needed [1]. Here, we provide a brief overview of that review article.

UO₂ fuel pellets are manufactured through a process known as sintering. In sintering, a powder is compacted to form a porous solid. This solid is then heated to a high temperature, but below the melting temperature, so the particles fuse together over time. It is a common, widely-studied practice in metals, ceramics, and plastics. Sintering is driven by the motion of atoms in the material. Atoms move from external surfaces to internal regions where particles are in contact. The overall effect is particles fuse together, eliminating most of the empty space between them, as illustrated below.

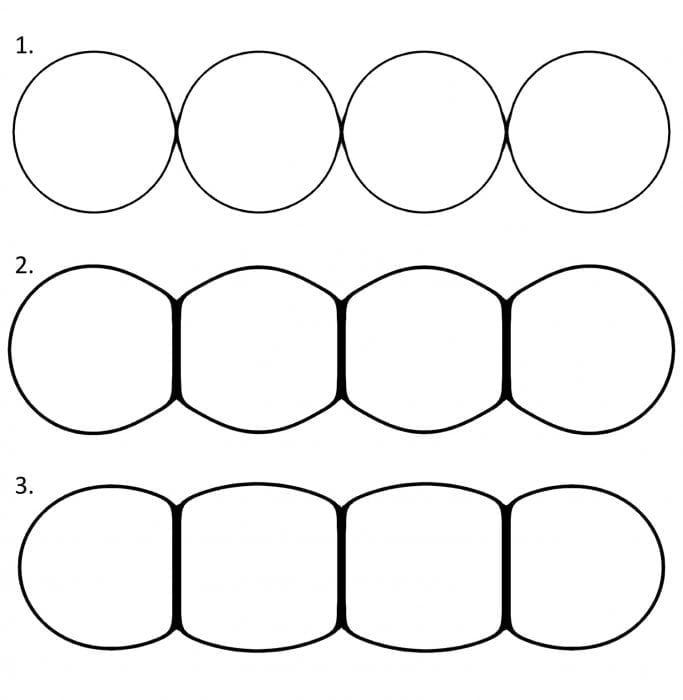
Credit: Ian Greenquist

Uranium fuel is sintered until the initially porous solid is eventually 95% to 97% dense, and is composed of relatively large crystals (around 10 microns across, so you need a microscope to see them) with pores scattered throughout. This microscopic structure is one of the biggest factors in how the fuel behaves; it impacts everything from how easily heat moves through the pellets to how much radioactive gas is emitted during operation. On top of that, there are countless variations of sintering that provide control over the structure. Factors that can be changed to control the microstructure include the time and temperature, the amount of oxygen present, the heating rate, and the presence of impurities.

However, before the process can be optimized, there is an important question that must be answered: What microstructure gives the best performance? In order to answer that, researchers can use computer models to predict how the fuel will behave in the reactor. Here too, sintering models are needed, because, in the intense heat and pressure of the nuclear reactor, the fuel pellets continue to sinter. Only this time, radiation speeds the process up.

Every time a uranium atom fissions, it splits into two smaller atoms which fly off in opposite directions with enormous energy. Since these atoms are inside of solid objects, they inevitably collide with other atoms, knocking those atoms out of place and causing them to fly off with enormous energy as well. A single fission product atom can knock thousands of other atoms out of place before the energy dissipates enough for them to settle down. These collisions speed up sintering in three ways. First, inside the cascades, the atoms move very quickly, and faster moving atoms mean more sintering. Second, the collisions cause some permanent damage which gives the atoms more space to move. This damage builds up throughout the entire material, increasing the overall rate of atom motion. Third, if the cascade happens near a pore, it can totally or partially destroy the pore by filling it in with other atoms.

Radiation damage combined with sintering is called irradiation-enhanced densification. Densification is an important process to model because it changes both the size of the fuel pellet and its structure.

Computer models that predict the UO₂ behavior during sintering and densification can be grouped into three basic categories: empirical, semi-empirical, and mechanistic. Empirical models come from running experiments, measuring the results, and then fitting some equation to give the same results. They are simple models that computers can run very fast, are relatively easy to develop, and give accurate results as long as you stay in the same conditions where you ran experiments. However, they tell researchers nothing about the physical processes causing the results. In some cases, experiments can be expensive and limit how many data can be collected. Finally, empirical models are not accurate outside of the range of conditions used in the experiments they are fit to.

Mechanistic models are detailed models built from our understanding of the physical processes involved [3]. Such an in-depth description reduces the need for fitting to data. They are more difficult to develop and can be harder to solve, but their predictions are driven by the underlying physics. Thus, they are more reliable for scenarios with few or no experimental data.

Semi-empirical models fall in-between the other two. They use both deterministic and empirical pieces to make a model with more physical understanding than an empirical model, but also easier to develop than a mechanistic one.

Models can also be categorized based on the size of the material that they represent. A model that predicts the behavior of the individual crystals and pores is called a microstructural model. These models tend to be too complex to simulate even an entire fuel pellet, but they give the most insight into what is happening to the pellet’s structure. A model that looks at the overall behavior of an entire fuel pellet is called a macroscale model. These models are more useful for design applications but have to make assumptions about what is happening at the microstructural scale.

Just to be clear: no type of model is the best in all situations. Different studies call for different models. A variety of models is necessary to give complete descriptions of sintering and densification.

Sintering modeling has converged to just three widely used models. The most common is the Master Sintering Curve (MSC). This is a semi-empirical macroscale model. The form of the equation is based on sintering physics, but several key variables must be determined through experiments. One of the key features of the MSC is that the form of the equation is the same no matter the material. The second sintering model is the Monte Carlo-Potts (MCP) model. This is a microstructural mechanistic model that works by replicating the random motion of atoms in the structure. The third is another microstructural mechanistic model called the Phase Field Sintering (PFS) Model. Unlike the MCP model, the PFS model uses differential equations to describe the overall motion of atoms.

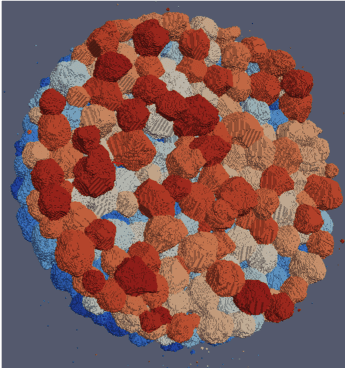
A Monte Carlo-Potts sintering simulation. Credit: Veena Tikare from Sandia National Laboratory

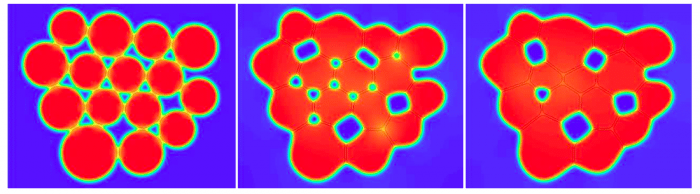
A Phase Field Sintering simulation. Credit: Michael R. Tonks

Since densification only occurs inside the fuel of a nuclear reactor, it has been studied much less than sintering. Plus, the safety concerns with radiation make experiments more difficult and expensive. As a result, computer models of densification are much less developed than sintering models. Because of this, there are seven commonly used densification models. All of these models are macroscale and either empirical or semi-empirical.

The lack of mechanistic and/or microstructural models of densification means that researchers are less able to determine how fuel will behave in a reactor and designing new fuel is that much more difficult. It is important to develop additional densification models that capture the microstructure scale and give a more complete deterministic explanation of the physics involved. One way to start solving this would be to take either the MCP or PFS and add radiation damage effects to it. Once such a model is developed, it would be the first densification model to be microstructural and to be mechanistic, and it would help researchers get a more complete understanding of how different fuels behave inside of nuclear reactors. With this information, the sintering process for fuel could be optimized to increase safety and decrease costs.

These findings are described in the article entitled Review of sintering and densification in nuclear fuels: Physical mechanisms, experimental results, and computational models, recently published in the Journal of Nuclear Materials. This work was conducted by Ian Greenquist from Penn State University, Michael R. Tonks from the University of Florida, and Yongfeng Zhang from the Idaho National Laboratory.

References:

1. I. Greenquist, M. R. Tonks, Y. Zhang, Review of sintering and densification in nuclear fuels: Physical mechanisms, experimental results, and computational models, Journal of Nuclear Materials 507 (2018) 381–395. doi:10.1016/j.jnucmat.2018.03.046.
2. B. J. Kellett, F. F. Lange, Thermodynamics of Densification: I, Sintering of Simple Particle Arrays, Equilibrium Configurations, Pore Stability, and Shrinkage, Journal of the American Ceramic Society 72 (5) (1989) 725–734. doi:10.1111/j.1151-2916.1989.tb06208.x. URL j.1151- 2916.1989.tb06208.x/abstract
3. M. R. Tonks, D. Andersson, S. R. Phillpot, Y. Zhang, R. Williamson, C. R. Stanek, B. P. Uberuaga, S. L. Hayes, Mechanistic materials modeling for nuclear fuel performance 105 11–24. doi:10.1016/j.anucene.2017.03.005.
   URL https://www.sciencedirect.com/ article/pii/S0306454916307423
4. S. Chen, Y. Xu, Y. Jiao, Modeling morphology evolution and densification during solid-state sintering via kinetic Monte Carlo simulation, Modelling and Simulation in Materials Science and Engineering 24 (8) (2016) 085003. doi:10.1088/0965- 0393/24/8/085003. URL 0393/24/i=8/a= 085003