Reducing Structural Vibrations With Unidirectional Composites

Vibrations of structural elements are often unwanted and disturbing. Not only do they reduce the service life of structures but also cause noise that can even affect health. Therefore, the reduction of structural vibrations is of continuing research interest.

To this end, polymer matrix composites have proven to be very well suited, as they can exhibit both high stiffness and damping qualities. Such composites are commonly employed in various applications, ranging from aircraft to high-end audio equipment. By dissipating the vibration energy, the structural vibrations, and hence the associated noise, are reduced. The damping performance can, therefore, be improved by adjusting the composite’s properties, for instance, the fiber volume fraction and the properties of the two component phases. And for rational design, it is essential to accurately predict the effective viscoelastic moduli of the composite from those of its constituents and the composite’s microstructure.

Our work describes a novel general, finite element procedure to estimate the effective viscoelastic stiffness of fiber reinforced polymer matrix composites. Here, unidirectional carbon/epoxy and glass/epoxy composites were studied.

The composite’s microstructure was modeled by periodic cells with aligned cylindrical inclusions. Up to 800 inclusions per cell were considered. The inclusions were dispersed with a Monte Carlo algorithm to create a random distribution. The effective viscoelastic moduli were then obtained from frequency-domain finite element simulations that were conducted in the COMSOL Multiphysics computational environment.

The fibers were assumed to be unidirectional and identical. However, in common industrial fiber composites, fibers are not identical but differ from each other in their diameters. Assuming typical fiber diameter distributions of industrial unidirectional composites, we generated and studied more realistic computer models containing fibers with different diameters. A comparison of the effective viscoelastic stiffness estimates obtained using this model to estimates for identical fiber composites showed that the effect of the fiber diameter on the effective moduli is practically non-existent.

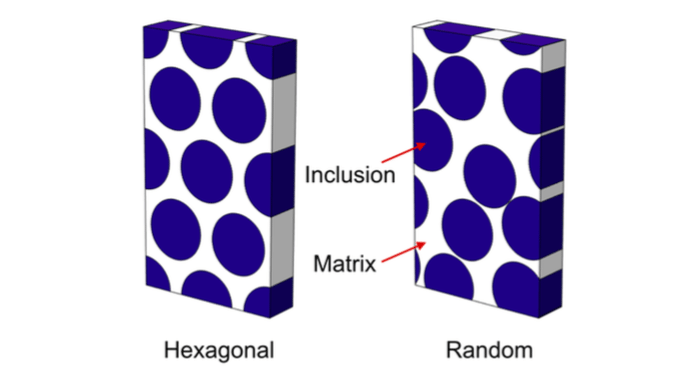
Figure 1: Computer models of fiber composites as used in finite element simulations. The periodic cells contain regular hexagonal arranged inclusions or randomly dispersed inclusions. Credit: Leyla S. Kern

We further compared the estimated effective stiffness with predictions of the classical three-phase cylinder model for carbon/epoxy composites. First, only finite element models with regular hexagonal microstructure were considered. It was found that both methods give remarkably close results, deviating by 2% at most. However, in more realistic models, fibers are randomly arranged, and, thus, simulations were repeated for models with randomly dispersed inclusions. The resulting effective moduli showed deviations of up to 10% from the three-phase composite cylinder model. For glass/epoxy composites, these deviations were even larger.

We concluded that the prediction of the three-phase cylinder model for viscoelastic composites is accurate for regular microstructures, but for more realistic random microstructures, the accuracy is decreasing, particularly for composites comprising glass fibers. However, the analytical model is still very useful for designers to capture trends and provide quick preliminary results for optimizing composite material combinations. Ultimately, the best quantitative predictions can be drawn from finite element estimates, which these days can be produced quickly and efficiently.

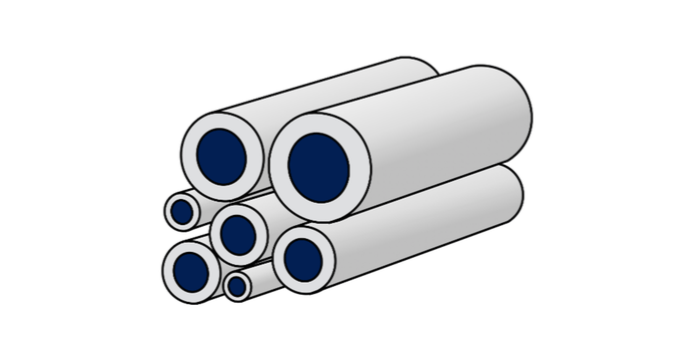
Figure 2: Illustration of the composite cylinder model. Credit: Leyla S. Kern

Further, vibration damping for structural applications was assessed. Strips from unidirectional composites with the previously determined effective viscoelastic stiffness were examined in cylindrical bending. It was found that higher fiber fractions caused an increase in the stiffness whereas the damping was severely impaired. As indicated by a figure of merit, we concluded that the overall damping performance is consequently reduced with higher fiber fraction.

The presented finite element procedure is a flexible and general tool for micromechanics design and optimization of composite material properties and fractions. It has the advantage over micromechanical models in that it can easily be used to study the effective viscoelastic stiffness of various shapes of inclusions (for instance platelets or short fibers) and is also applicable to other homogenization problems.

These findings are described in the article entitled, Frequency domain finite element estimates of viscoelastic stiffness of unidirectional composites, recently published in the journal Composite Structures. This work was conducted by Andrei A. Gusev and Leyla S. Kern from ETH Zürich.