Reactive Solute Transport In An Asymmetrical Fracture-Rock Matrix System 

Understanding reactive solute transport in a single fracture-rock matrix system is the basis for studying transport behavior in the complex fractured porous media. Quantification of solute transport in the fracture system is essential for assessing the long-term fate of solute transport and characterizing the contamination redistribution. With asymmetrical transport properties in the rock matrixes, reactive solute transport in the single fracture-rock matrix needs to be treated as a coupled three-domain problem.

Previously, Zhu et al. (2016) provided an analytical solution for solute transport in the fracture-matrix system without considering dispersion. Zhou et al. (2017) examined the solute transport in a filled fracture-matrix system with symmetric transport properties. The goal of this study is to construct a fully coupled model to deal with the transport problem in a single fracture-rock matrix system with an asymmetrical distribution of transport properties in the rock matrixes. Advection and dispersion along the single fracture, diffusion in the rock matrix and radioactive decay and adsorption in the entire system are considered in this model.

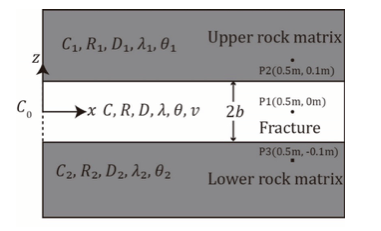
Figure 1. The conceptual model of the single fracture-rock matrix system.

The simulated models demonstrated that the concentration in the fracture is not sensitive to the asymmetrical distribution of transport properties in rock matrixes compared to the symmetric case. However, concentration distribution and mass stored in rock matrixes are directly associated to how the transport parameters are distributed in rock matrixes: A larger matrix porosity and a higher diffusion coefficient in the matrix will lead to a higher level of concentration in the matrix. Also, a greater diffusion coefficient in the rock matrix means a better ability to store more mass at the same time.

To study the effects of the diffusive mass exchange among different domains, a water flushing phase is applied to the left boundary after a certain time. The simulated results indicate that the asymmetrical distribution of transport properties in the rock matrix has significantly impacted on the transport in the rock matrix. However, the transport in the single fracture is only slightly affected. The solute mass stored in the fracture has qua ick response to the timing of flushing phase. Meanwhile, the mass stored in the rock matrix is not sensitive to the flushing phase, which has an obvious delay.

The main contribution of this study is that it constructs a fully coupled model for the single fracture-rock matrix system with the consideration of asymmetric nature in the upper and lower rock matrixes. The improvement over classical research makes it possible to quantify the transport processes in fissures with different rock bodies or unconformity. Since the similarity between solute and heat transport in porous media, the newly developed model also can be applied to examine heat transport problems, which can be used in some practical scenes, such as the development of hot-dry-rock geothermal energy.

However, this study also has its own limitations for the further investigation. The parameters here are assumed to be time and scale independent, which may not be true in reality. The dispersivity in the fracture was reported as a scale-dependent parameter in some studies while the diffusion coefficient was claimed to be time-dependent. Also, the model is built based on an idealized single fracture. However, if the single fracture has an irregular trajectory, a different method would be needed to rebuild the model.

These findings are described in the article entitled Reactive solute transport in an asymmetrical fracture–rock matrix system, recently published in the journal Advances in Water Resources. This work was conducted by Renjie Zhou and Hongbin Zhan from Texas A&M University.

References:

1. Zhou, R.J., Zhan, H.B., 2018. Reactive solute transport in an asymmetrical fracture–rock matrix system. Adv. Water Resour., 112: 224-234. DOI:10.1016/j.advwatres.2017.12.021
2. Zhou, R.J., Zhan, H.B., Chen, K.W., 2017. Reactive solute transport in a filled single fracture-matrix system under unilateral and radial flows. Adv. Water Resour., 104: 183-194. DOI:10.1016/j.advwatres.2017.03.022
3. Zhu, Y.H., Zhan, H.B., Jin, M.G., 2016. Analytical solutions of solute transport in a fracture-matrix system with different reaction rates for fracture and matrix. J. Hydrol., 539: 447-456. DOI:10.1016/j.jhydrol.2016.05.056