
Recent advances in quantum computing along with increased interest in solving difficult optimization problems is shining a light on a research area that has been quietly growing for the past twenty plus years.
This area involves modeling difficult decision problems as Quadratic Unconstrained Binary Optimization (QUBO) problems and then solving them on a new type of quantum computer using qubits. D-Wave Systems is currently the only company building commercially available quantum computers. D-Wave employs quantum superposition and entanglement between qubits (analogous to binary digits, or bits) that can be both 0 and 1 at the same time. This allows them to effectively explore an unimaginably large solution space. In addition, the D-Wave’s unique architecture allows it to solve QUBO very efficiently.
For the past half-century operations research (which focuses on mathematical modeling and optimization) has relied on concepts associated with linear programming (LP) using the simplex method developed by George Dantzig in the late 1940s. However, many real-world problems are neither linear nor continuous, as required for LPs. Non-linear, discrete problems modeled as quadratic problems (QP) can be effective when two variables interact with one another, or are highly correlated. A QUBO is a subclass of QP where the variables are binary (0/1, yes/no, on/off, -1/+1, and so on) and there are no constraints (or the constraints can be absorbed into the unconstrained formulation by clever representation techniques, often utilizing penalties for constraint violations).
The exponential growth in computer processing power along with cheap memory have allowed LP solvers to run some quadratic optimization models, but the conversion process from QP to LP can result in LPs that are too large to be solved within practical time limits. A dramatic example of this is the generalized vertex cover problem (GVCP), which is an extension of the classic vertex cover problem. The goal is to find a minimum cost subset of the nodes in a graph such that every edge in the graph is incident to at least one of the chosen nodes. For example, if all nodes have the same cost, then nodes 1 and 2 optimally cover the graph below because every edge is incident to either node 1 or 2.
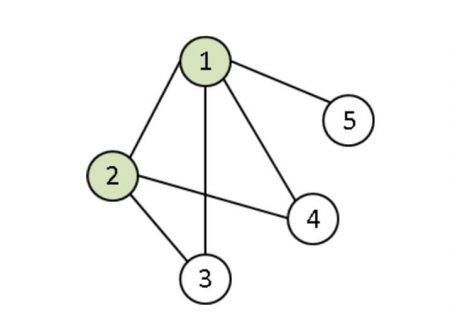
GVCP adds edge costs to the problem, where the cost of not including an edge is higher than including only one endpoint of the edge, and the lowest cost solution includes edges with both endpoints covered. A linear programming model of a 5000 node GVCP can have over 21 million variables and 31 million constraints! A problem of that size requires a lot of time even for the most powerful supercomputers. By contrast, an equivalent QUBO model has only 5000 variables and no constraints and QUBO problems of this size have been readily solved on standard PCs. Although this size problem is too large for the currently available quantum computers, larger and denser quantum chips are being designed.
What sort of problems are amenable to quantum annealing computers such as the D-Wave? There are many general business and science areas that could see benefits. In addition, there are multiple broad classes of mathematical problem types that are classified as hard (technically they are non-deterministic in polynomial time) with broad application. For a summary of QUBO methods and applications see the survey paper listed in the reference section.
| Areas with QUBO components: | Some established QUBO problem categories: |
| Finance & Portfolio optimization | Ising spin glass |
| Project Selection | Satisfiability |
| Cluster Analysis | Max-cut |
| Economic Analysis | Two machine scheduling |
| Traffic Management | Max clique |
| Circuit Board Design | Set Partitioning |
| Robust Business Decision making | Max 2-sat |
| Protein Folding | Maximal Independent Set |
| Network Design | Linear Ordering |
| Website traffic analysis | Task Allocation |
| Social network & link analysis | Vertex Coloring & Covering |
| Fault generation for SW testing | Sum Coloring |
| Image analysis | 2-TAP (task allocation problem) |
| Prediction of epileptic seizures | Quadratic knapsack |
As good as this sounds, there are serious obstacles to overcome when solving QUBO on quantum computers such as the D-Wave. Problems that can be directly solved on a current D-Wave system are limited by the number connectivity of the qubits, meaning that QUBO problems with 2000 decisions (qubits) and a large number of quadratic correlations are not directly solvable via quantum entanglement. However, software tools exist that partition large QUBO so they can be solved on a D- Wave system and improvements in software tools and coming generations of D-Wave computers are in the works.
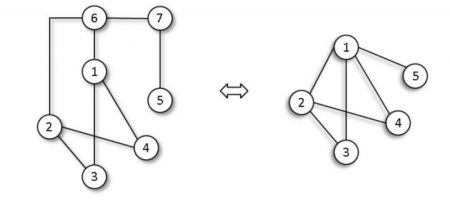
One group of researchers, led by Gary Kochenberger and Fred Glover at the University of Colorado, have a long history of finding transformations from LP to QUBO and are now investigating QUBO-to-QUBO transformations. Their latest research published in the journals Networks and the European Journal of Operational Research derive multiple rules for transforming a given QUBO to an equivalent QUBO with fewer variables. For example, QUBO problems with 10,000 variables and certain natural network properties have been reduced to equivalent QUBO with less than 100 variables. Unlike the graph morphology transformations used in image processing which are very difficult, inexact and time consuming, these new rules are very fast and exact. A goal of the research is to be able to transform a given QUBO into one that exactly matches the capabilities of a D-Wave. Due to the difficulty of this problem, carefully designed heuristic approaches offer the greatest promise for future advances.
References
- Mark Lewis & Fred Glover, 2016. Binary Quadratic Network Preprocessing: Theory and Empirical Analysis. Networks, doi:10.1002/net.21751.
- Fred Glover, Mark Lewis, Gary Kochenberger, 2017. Logical and Inequality Implications for Reducing the Size and Difficulty of Quadratic Unconstrained Binary Optimization Problems, European Journal of Operational Research, doi.org/10.1016/j.ejor.2017.08.025.
- Kochenberger, G. et al., 2014. The Unconstrained Binary Quadratic Programming Problem: a Survey. Journal of Combinatorial Optimization, 28(1), pp. 55-81.
This article is based on the recent study, Quadratic Unconstrained Binary Optimization Problem Preprocessing: Theory and Empirical Analysis, by Mark Lewis and Fred Glover.








