One-way Sound Propagation: Breaking Acoustic Reciprocity In 2D Materials

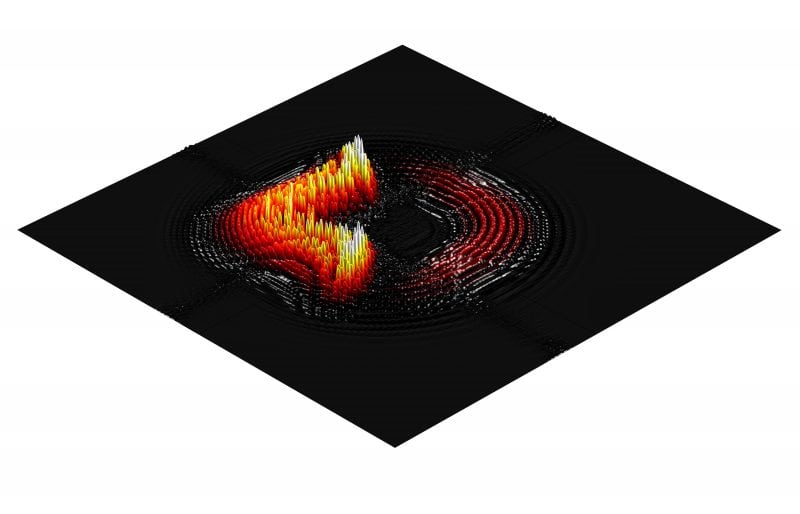
Phononic materials with elastic or acoustic fields that travel simultaneously in space and time have been shown to break elastodynamic reciprocity culminating in intriguing asymmetric, and often unidirectional, wave propagation patterns. In this work, wave dispersion in finite two-dimensional (2D) thin membranes excited at the center with an omnidirectional source is investigated.

Owing to the periodic nature of the material arrangement, such systems exhibit what is referred to as phononic band gaps, i.e. frequency ranges within which incident waves are not able to propagate the material’s medium as a result of Bragg scattering effects. Upon imposing an external modulation of material properties that forces them to travel in space and vary in time, assumptions governing the fundamental reciprocity theorem are no longer in place. As a consequence, waves traveling from point A to B do not follow the same pattern when traveling from B to A.

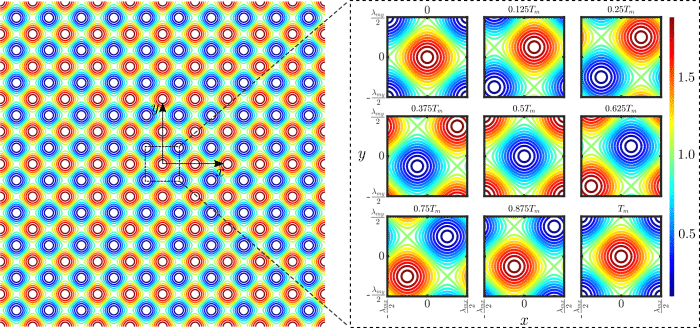
Figure 2: Schematic of a thin membrane with a periodic material field (left). A close-up of an individual cell and the evolution of material properties with time over one complete cycle (right). Credit: Mostafa Nouh

In dispersion physics, this translates into band structures which are asymmetric about the wave number origin. Breaking the symmetry of such band structures creates a dispersion bias that serves to force waves to travel asymmetrically in opposing directions. The outcome is a wide range of acoustic systems that can manipulate input excitations in ways that make forward and backward traveling waves non-identical. Combining the previous concept with the ability of such periodic materials to demonstrate band gaps, the possibility of band gaps that span different frequency ranges in two opposite directions becomes feasible.

By driving the material at a frequency that lies within a predicted one-way band gap range, unidirectional wave propagations can be exploited. In effect, the material allows waves to travel without interruptions in confined angular directions while impeding the same waves from flowing in the opposite ones.

Motivated by this, we introduce a non-reciprocity index (NRI) that quantifies the degree of non-reciprocity in every propagation direction of the 2D membrane. The developed NRI is defined as a function of the propagation direction (α) and temporal modulation frequency (γ_m). It is defined such that for a time-invariant membrane (and thus perfectly reciprocal), the NRI reduces to zero irrespective of the propagation direction.

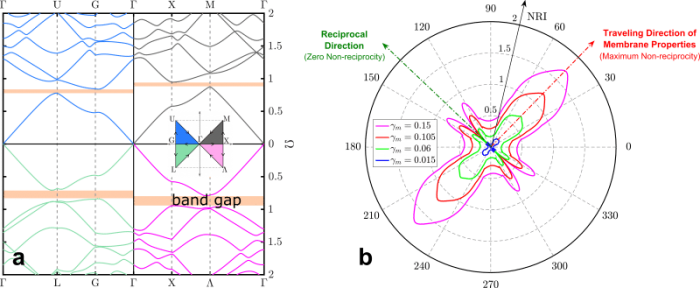
Figure 3: (a) Non-reciprocal band gaps in the dispersion characteristics of a membrane with material fields traveling simultaneously in space and time. (b) Variation of the Non-reciprocity Index (NRI) with different wave propagation directions. Credit: Mostafa Nouh

By looking at NRI maps, it can be inferred that the traveling direction of the material properties dictates the degree of non-reciprocity within the 2D space of the membrane. As anticipated, the degree of non-reciprocity reaches a maximum value in the traveling direction of the properties and completely vanishes in the perpendicular direction thereof. This can also be explained in light of the medium that the waves face as they propagate in each direction. From their perspective, waves propagating opposite to the traveling direction of the material field can only see the spatial and not the time-variations of the modulations of the membrane properties and thus disperse symmetrically in both forward and backward directions.

The previous opens up possibilities for acoustic filters or tunable mechanical switches that operate analogously to electronic components. Furthermore, the same concepts can trigger transformative enhancements in a wide array of technologies, especially in the domain of biomedical imaging and acoustic tomography, where state of the art devices suffer from detrimental image artifacts caused by reflections from receivers.

The question, however, remains: How can such material modulations be achieved in simple and cost-effective ways? As of now, there is not a clear – commercially viable – answer to that challenge, although adaptive materials such as piezoelectrics and magnetoelastic materials pose as promising candidates for such avenues.

These findings are described in the article entitled Non-reciprocal elastic wave propagation in 2D phononic membranes with spatiotemporally varying material properties recently published in the Journal of Sound and Vibration. This work was conducted by M. A. Attarzadeh and M. Nouh from the University at Buffalo, SUNY.