
The twisting somersault is a visually stunning acrobatic maneuver featured in numerous Olympic sports, such as platform and springboard diving, gymnastics, and aerial skiing. It is therefore not surprising that sports coaches are seeking to gain insight into the biomechanics behind the aerial maneuvers associated with a good somersault, in order to better train their athletes and equip them with a leading edge in competition.
The analysis of the twisting somersault poses an interesting problem in classical mechanics. How can an athlete take-off in pure somersaulting motion, initiate twisting mid-flight, and then return to pure somersaulting motion? To answer this question, mathematicians at the University of Sydney developed a mathematical model to simulate and optimize various somersaults in platform diving. Their research led to the discovery of a new innovative dive consisting of 1.5 somersaults and 5 twists, a dive so complex that the International Swimming Federation has yet to assign a degree-of-difficulty to the dive. Through numerical optimization and simulation, they demonstrate that such a dive is theoretically possible and can be performed from the 10m platform. It is hoped that one day an athlete will perform the prescribed dive in competition.
The classical formula linking the angular momentum vector L, angular velocity vector Ω, and tensor of inertia I is given by L=IΩ. This formula is specified in the body frame, meaning the quantities are measured relative to the athlete and not from an external observer. The angular momentum vector after take-off is constant for an external observer, but for the athlete in the body frame, only the total angular momentum given by the magnitude of the vector is constant. This results in an angular momentum vector lying on an L-sphere, where the radius is the magnitude of the vector.
In platform diving, the athlete takes off in the layout position shown in Figure 1a. For the simpler class of somersaults without twist, the athlete performs symmetric shape changes to move into and out of pike or tuck position. During shape change the moments of inertia change in value, but principal axes of inertia remain constant in direction. This also means the angular velocity vector only changes in magnitude but not in direction. The pure somersault without twist results in a steady rotation, where the angular momentum vector remains stationary on the L-sphere.
There are in total six equilibria on the L-sphere as shown in Figure 2. An equilibrium on the L-sphere corresponds to a steady rotation about a principal axis. With our chosen convention the two equilibria on the Ly axis correspond to forward and backward somersault (Figure 1a), equilibria on the Lz axis correspond to clockwise and counterclockwise twist (Figure 1b), and equilibria on the Lx axis correspond to the two directions of cartwheel (Figure 1c). Motions starting at any of these six equilibria will result in steady rotation, but initiating it at any other point will result in trajectories that move around the L-sphere.
The principal moments of inertia in ascending order by magnitude correspond to rotations around the twist axis, somersault axis, and cartwheel axis. The intermediate axis theorem states that rotations around its first and third principal axes is stable, while rotations around the second axis is unstable. Initiating at a point near the poles of the Lx and Lz axes will result in small perturbations around that rotation axis, but the rotation will otherwise remain bounded. On the other hand, initiating at a point near the pole of Ly will not bound the orbit to lie within a neighborhood around the equilibrium, instead, the trajectory will traverse around the L-sphere before returning. As the somersault axis is unstable, this explains why athletes taking off in pure somersaulting motion can easily transition into twisting somersaulting motion mid-flight, and then stop the twisting motion just before completing the dive when the trajectory returns.
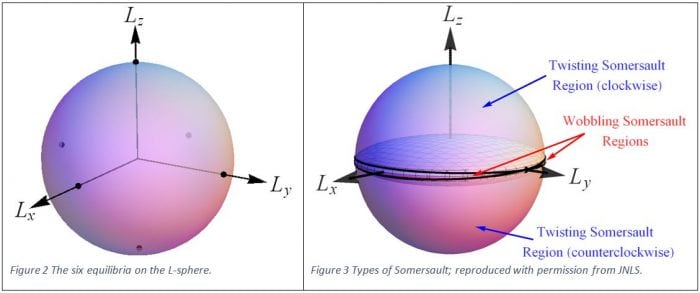
Orbits on the L-sphere can be classified as being either a wobbling somersault or twisting somersault. The wobbling somersault occurs when the athlete somersaults about a horizontal axis but also has an oscillatory twisting motion that causes the body to twist one way and then the other.
The twisting somersault, on the other hand, occurs when the twisting motion is always in the same direction. Animation of the wobbling somersault is in shown in movie 1, and for comparison, the twisting somersault is shown in movie 2.
For twisting somersaults, the further the orbit from the equator, the faster the twist. The limit occurs when the orbit becomes a point corresponding to a pole on the Lz axis, where the motion reduces to pure twist without somersault. Due to the conservation of angular momentum, a faster twist results in a slightly slower somersault. The somersault is only slightly slower because the component of the tensor of inertia about the somersault axis is much larger than the component in the twist axis. This is demonstrated in movie 3 where two different twisting somersaults are compared that have the same total angular momentum and tensor of inertia.
It is now clear that the pole at Ly results in a pure somersaulting motion (in the forward direction) and an orbit below the equator results in twisting somersaults (in the counterclockwise direction). To transition from one state to another, the athlete performs an asymmetric shape change, such as lowering of the left arm. The athlete can then hold the twist position to accumulate the desired number of twists before raising their arm again to stop the twist. The number of twists corresponds to the number of times the trajectory loops around the L-sphere, and the amount of somersault is related to the total area enclosed by the orbit and equator.
A twisting somersault consisting of 1.5 somersaults and 3 twists is demonstrated in the supplementary materials of an earlier paper Twisting Somersault, where the basic diving mechanism consists of 5-stages:
- pure somersault – athlete takes off in layout position
- shape change – athlete moves into twist position
- twisting somersault – athlete holds the twist motion
- shape change – athlete moves back to the layout position
- pure somersault – athlete finishes off the dive
The intuition behind squeezing additional twists in the same amount of time lies in the fact that the twist rate is faster if the orbit is closer to the south pole (for counterclockwise twists). So rather than using the second shape change to stop the twisting motion, the athlete can instead use the second shape change to speed up the twist. The only caveat is that the athlete is now in a faster twisting somersaulting state, and the twisting motion cannot be terminated directly. The athlete must first perform a shape change to slow down the twist, and then perform another shape change to stop the twist. The traditional 5-stage dive becomes a 9-stage dive, where the steps are:
- pure somersault – athlete takes off in layout position
- shape change – athlete initiates the twist
- twisting somersault – athlete waits for the transition
- shape change – athlete enters the faster twisting somersault
- faster twisting somersault – athlete holds the twist position
- shape change – athlete slows down the twisting motion
- twisting somersault – athlete waits to terminate twist
- shape change – athlete terminates twist
- pure somersault – athlete finishes off the dive
It is simulated that performing the described dive enables the athlete to squeeze in 1.5 somersaults with 5 twists from the 10m platform. If such a dive is ever performed in competition it will revolutionize the sport of diving. The complexity of the dive is in the timing of the shape changes, where the second shape change must be appropriately timed after a half orbit to maximize the new twisting speed. Performing it at the wrong time will not provide maximum benefit, may make the twisting slower, or even worse could leave the athlete in the wobbling somersault phase.
The third shape change must also be precisely timed to undo the second shape change, in order to return the athlete to the original twisting somersaulting state. Otherwise, the athlete will be unable to stop the twisting motion as they enter the water, which could result in serious injury when diving from the 10m platform. For these reasons, no athlete has ever attempted a dive with 1.5 somersaults and 5 twists. However, through mathematical modeling and simulation, the maneuver is shown to be possible and would revolutionize the sport of diving if successfully performed in competition. A simulation of the dive is shown in Movie 4.
These findings are described in the article entitled A New Twisting Somersault: 513XD, published in the Journal of Nonlinear Science. This work was led by William Tong & Holger R. Dullin from The University of Sydney.








