Minima Of Radiated Acoustic Power Are Different From Structural Vibration

Structural vibration mechanism and control have been studied deeply over the last several decades. As the dynamic characteristics usually can be expressed in the form of natural frequencies (poles), antiresonances (zeros) or minimum response frequencies, it is an effective way to change the peaks and valleys of vibrating response by assigning desirable poles to avoid resonances or assigning zeros to certain locations. Although the mechanism of generation of sound is by structural surface vibration, they are different in some ways.

So we pay attention to the characteristics of structural acoustic radiation and try to obtain their poles and minima. Taking the structural dynamics information into account, we developed a formulation so that the poles and minima can be obtained directly through solving a polynomial equation. Besides, we discussed the relationship between the minima of radiated acoustic power and the antiresonances of vibration response.

Fig.1. The radiated acoustic power of a plate. Republished with permission from Elsevier from: https://doi.org/10.1016/j.apacoust.2017.10.020

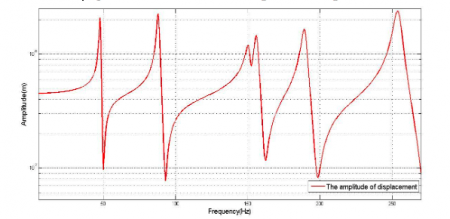
Fig.2. The Frequency response function of the plate at the excitation location. Republished with permission from Elsevier from: https://doi.org/10.1016/j.apacoust.2017.10.020

Fig.1 and Fig.2 show the responses of sound radiation power and displacement of a vibrating plate, respectively. It can be seen that the radiated acoustic power from the developed formulation is largely coincident with the previous research, and their poles and minima can be read from Fig.1. The poles are corresponding to the highest levels of the radiated acoustic power and the minima are corresponding to the lowest levels. So one can estimate the maximum, the minimum and the shape of the acoustic power radiated from a vibrating structure in the frequency range of interest.

We also find that the poles of the acoustic power are coincident with the natural frequencies of the vibrating structure. In other words, the amplification of radiated acoustic power occurs when the excitation frequency approaches the natural frequency.

This result can be explained in the view of structural vibration: the resonances of a structure are ‘global’ parameters (i.e. the same resonances are expected to appear on any Frequency Response Function of the structure), and then the global response will increase when the excitation frequency is close to the resonance frequency, therefore, the acoustic power radiated from the vibrating structure will increase as the input frequency is approaching to a natural frequency and decrease as the input frequency is moving away from the natural frequency.

For the minima of the acoustic radiation power, they might be different from the zeros of the structural vibration between two adjacent poles, that is to say, when the input frequency is a zero of the vibrational response, it may not be a minimum of the radiated acoustic power and this result is affected by the modal radiation efficiencies and the mutual radiation between these adjacent modes.

In addition, the obtained poles and minima can be used to describe the shape of the radiated acoustic power in the frequency range of interest. Also, the poles and minima assignment of the radiated acoustic power may be applied in the structural acoustic control.

These findings are described in the article entitled The poles and minima of radiated acoustic power from plate vibration, published in the journal Applied Acoustics. This work was led by Sheng Li and Maolong Xia from the Dalian University of Technology.