Exploring Spatial Representation In Artificial Intelligence Systems

Artificial Intelligence has made great progress in the last decade, in particular, thanks to recent developments in machine learning. As a consequence, we often read in the news that artificial systems now perceive the world as we do and sometimes even outperform humans in some specific tasks. However, are these claims justified?

Looking more thoroughly at the intricate machinery making these achievements possible, one quickly realizes that they heavily depend on human supervision. Of course, engineers are necessary to develop and implement machine learning algorithms in the first place. But more importantly, human input is also required to interpret the data that will be fed to the system.

In other words, a human has to go through the data, extract some meaning out of it, and encode it in a numerical format that the learning system can process. Likewise, it is also a human who interprets the results produced by a machine learning system and associates some meaning to its numerical output. In between those two humans interpretations, the system performs some data processing in which the semantic content seems to be of little importance if any.

Thus, today’s AI systems rely on humans to deal with the content of perception. Of course, this induces practical issues. Exponentially more human input is required as the range of applications widens, and no elegant solution exists yet for AI systems to adapt to new environments or tasks autonomously. This is why today there is an active “unsupervised learning” front in the machine learning community. Its goal is to push AI systems towards more autonomy, by identifying patterns in raw data and/or interacting directly with the world to make sense of it, instead of relying on human inputs.

There is, however, an ongoing debate in the community about how to proceed. In particular, it is not clear how many *priors* have to be hard-coded in the learning system. These priors correspond to any structural information about the data/task that engineers implement in the system before it is even turned on. For instance, convolutional neural networks, which have proven to be very successful in dealing with images, contain very strong priors regarding the image structure of the data: the neural network is implemented such that the system “knows” that the input has a regular 2D structure, such that 2D filters can be convoluted with it to perform a consistent spatial operation. Without this prior knowledge, a standard neural network (fully connected) has great difficulty performing the same task, as it has way more possibilities to process the input.

Think of it as learning an alien language from scratch. With no a priori knowledge, this is quite a complicated task (see for instance “Story of your life” by Ted Chiang, which inspired the movie “Arrival”). It might, however, be a bit more manageable if you are first informed that, like us, those aliens use nouns, verbs, and adjectives. And it gets even easier if you’re informed that the penultimate word is always the verb. This is what priors do. They make the learning task easier by reducing the space of hypothesis to explore.

So, do robots need priors? Given the astronomical number of ways the raw data they have access to (sensors, motors, memory…) can be processed, it seems like some priors are required. After all, our own brain does not appear as a blank slate when we are born. In machine learning, this is well illustrated by model-free reinforcement learning approaches which require a gigantic amount of data to solve a task defined in a limited space of possibilities (see OpenAI Five and it’s 180 years of playing per day). It doesn’t look like such largely prior-free methods can scale to real-world problems easily. But given that attempts to symbolically model cognition have failed in the past decades, how much priors should we put in the system to not hinder its learning capacities? The question remains open.

One way to answer the question is to take a radical stance: How far can we go without any human prior? Can an AI system develop its own kind of perception on its own?

According to the Sensori-Motor Contingencies Theory (SMCT), this might be possible. The central claim of this theory is that perception does not primarily rely on the passive processing of sensory inputs but on the processing of the sensorimotor flow. Indeed the interaction between an AI system (let’s say a robot) and the world can be seen as a dialogue, mediated by the sensorimotor channels. When the agent “says” something by sending a motor command, the world “answers” by providing a sensory variation. But of course what is interesting is that the answer is not random. The world is highly structured and so is its answer.

For instance, every time you hit a wall, the world sends you a tactile feedback. Every time you shout, you can hear yourself. Every time you look at a car and blink, the car stays the same.
Contrarily to traditional approaches of perception which focus primarily on the sensory input, SMCT-based approaches look for these regularities in the sensorimotor flow. And according to the theory, it might be possible for a naive robot to develop perception by exploring the world and identifying these regularities. The idea sounds appealing, but what regularities are we talking about exactly?

In the past few years, we worked with colleagues on answering this question for a specific facet of our perception: space. The perception of space is indeed a fascinating problem. It is pervasive in our understanding of the world — most of what we perceive is embedded in space — and it appears to be an abstract notion that goes beyond the mere properties of the objects that surround us at any time. Yet its fundamental nature remains a mystery.

Of course, this did not stop roboticists from solving spatial tasks (that is to say, almost all robotics applications). But for that, they need to introduce strong priors about the nature of space. Usually, the task is a priori defined in terms of Cartesian coordinates [x,y,z], the robot’s configuration is defined in terms of positions and orientations, the responses of the sensors to spatial phenomena are modeled a priori (for instance, a raw laser sensor reading is interpreted as a distance), and so on. Our objective was to investigate the possibility for a naive robot to come up with equivalent spatial knowledge without any prior.
To do this, we took inspiration from great mathematicians and philosophers of the past, like H.Poincré and J.Nicod, who already explored this question. Poincaré, in particular, had a brilliant insight: for a tabula rasa brain, perception of space should emerge from the experience of *compensation*.

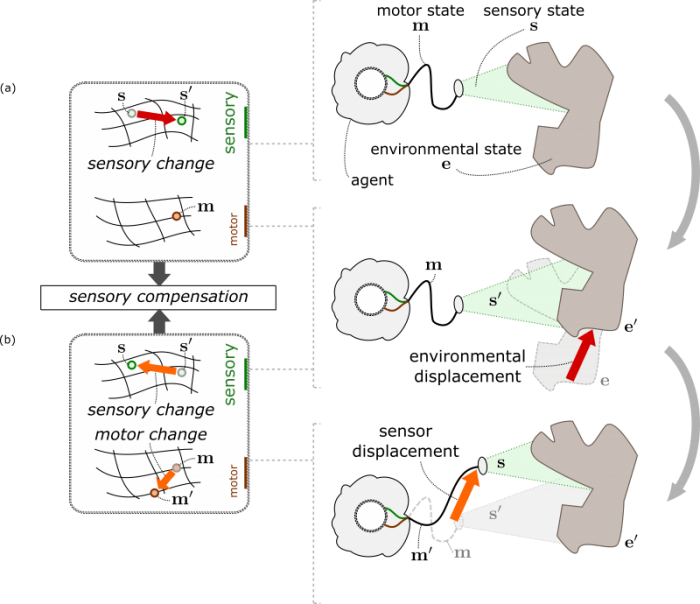
An abstract representation of an artificial agent observing an object. When the object moves, it generates a sensory change that the agent can compensate for by moving its own sensor. These “compensation” episodes are the internal imprint of spatial transformations (displacements). Republished with permission from Elsevier from: https://doi.org/10.1016/j.neunet.2018.06.001

A compensation is a specific sensorimotor experience which occurs when an object and the agent observing the object both undergo the same displacement. Imagine, for instance, that you are looking at an apple. The apple is projected on your retina and produces a specific pattern of excitation of your photoreceptor cells. Now let’s assume that the apple moves to the right. It now occupies a different part of your field of view and produces a different excitation pattern on your retina. Yet, it is possible for you to also move to the right, find the same relative position to the apple as before, and re-experience the exact same initial sensory input once again. This is a *compensation*. By sending a motor command, you were able to cancel the sensory change produced by a displacement in your environment.

Why is such a compensation episode so remarkable, and why is that related to space perception? First, no a priori knowledge about the agent’s body, its sensors, its motors, its environment, or space is necessary for a compensation to be experienced. The compensation phenomenon holds regardless of the particular sensorimotor apparatus of the agent. Second, for a naive agent, the occurrence of such a compensation episode is highly noteworthy in a flow of data which otherwise spreads everywhere in its high-dimensional sensorimotor space. Third, compensation episodes exhibit particular spatial-like properties. Like space, which always appears the same regardless of the objects embedded in it, compensations are “content-independent”: an equivalent compensation could happen with a pear or a pen in place of the apple. Like space, which appears to be “shared” by us and objects around us, compensations are shared by the agent and objects around it, as they both play a symmetrical role in the phenomenon.

Finally, like space which appears to be “isotropic” (it keeps the same structure everywhere), compensations can happen in the same manner regardless of the position and orientation of the agent. Fourth, compensation episodes occur when the object and the agent undergo spatial changes (be it translations or rotations) but not for other kinds of changes. For instance, an agent is able to compensate for a car moving to the left, but not for a car changing its color, or its weight. Conversely, no change in the environment could compensate for a non-spatial action of the agent, such as changing its internal temperature or uttering a sound. Compensations only apply to displacements of the agent and its environment, which are by nature spatial. As such, sensorimotor compensations appear to be the way for a naive agent to ground the notion of space by discovering the existence of particular changes in the world which correspond to displacements.

In a recent paper published in Neural Networks (Discovering space — Grounding spatial topology and metric regularity in a naive agent’s sensorimotor experience), we formalized Poincaré’s intuition and analytically described how a simple robot could discover the sensorimotor regularities induced by space via compensation episodes. To do this, we let the robot actively observe an object that can move in the environment. By discovering the subset of motor transformations associated with compensation episodes, the robot can first capture the topology of the external space in which it is moving with the object. In the process, it discards any redundancy of the motor apparatus by representing as a unique “point of view” all redundant motor states which lead to the same spatial configuration of its sensor.

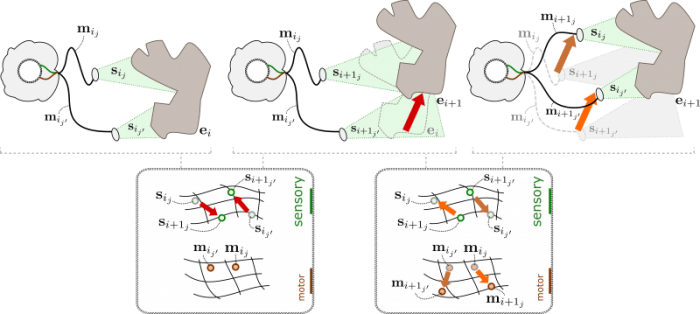
Compensation episodes can happen from multiple points of view. As a consequence, the agent can discover that different motor changes correspond to the same external displacement. Republished with permission from Elsevier from: https://doi.org/10.1016/j.neunet.2018.06.001

By then continuing to observe the moving object from multiple “points of view”, we showed how it is theoretically possible for the robot to capture the metric regularity of the external space by discovering that a single displacement of the object can be compensated for by different motor transformations corresponding to different points of view on the object. As a result, it is possible to construct from raw sensorimotor experiences an internal encoding of the motor states which accurately represents the topology and metric of the robot’s spatial configuration.

These results are of theoretical interest, but also offer some philosophical insight on the question of space perception. Indeed, both the motor and sensory components of a robot’s experience seem necessary to extract spatial transformations from the rich sensorimotor flow. Without an active exploration of the environment and the experience of sensorimotor compensations, no notion of space would emerge. Moreover, the notion of space could be “truncated” by limited motor capacities. Despite the external space having its own structure, the robot might only be able to partially capture it if it is unable to move in specific directions, and thus unable to compensate displacements of objects along those directions. A bit like a rotating 4-D cube appears to us as changing its appearance, any displacement of objects along non-compensable directions would appear to the robot as a non-spatial change, but appearance change.

Leaving aside these philosophical considerations, we decided more recently to investigate how relevant these theoretical results were in a machine learning context. In the paper “Unsupervised Emergence of Spatial Structure from Sensorimotor Prediction,” we designed a simple experimental setup to assess if a neural network would indeed capture the sensorimotor regularities induced by spatial experiences.
Our working assumption was that capturing spatial sensorimotor regularities is beneficial for sensorimotor prediction. The intuition is that if the robot has discovered that two motor changes have been associated with the same sensory changes, they might be associated with the same external displacement. In which case, internally representing these two motor changes the same way offers the predictive advantage that any new sensory experience produced by one can be extrapolated as true for the other.

We thus proposed a simple neural network architecture to perform self-supervised sensorimotor prediction. The network takes as input a current sensory state and a current motor states and tries to predict the future sensory state given a future motor state. To do so, the motor states are encoded into an intermediary representation on top of which the prediction is performed. The whole network was optimized end-to-end without constraining in any way how motor states are encoded in the intermediary representation.

We collected data by letting a simple robot explore a moving environment in several different ways. They differed in that the sensorimotor data fed to the network during training were consistent or inconsistent with an actual spatial exploration of the environment. You can think of the inconsistent condition as feeding the network with exploration data in a random order. On the contrary, in the consistent condition, the network was fed with the spatiotemporally consistent sequences of sensorimotor states collected during the exploration. In this second case, the robot should experience compensation episodes from multiple points of view, and we hypothesized it would results in spatial structure (topology and metric) being captured in the intermediary motor representation.

This is indeed what happened. Although the network organized the motor representation in an arbitrary way when the data is not consistent with a spatial exploration, the motor representation built from spatially consistent data captures both the topology and metric regularity of the external space. In other words, without any a priori knowledge about its sensorimotor apparatus, and without any specifically-tailored priors about the motor representation, the drive for good sensorimotor prediction was sufficient for the robot to build a reliable internal proxy of its external spatial configuration.

These results shed an interesting light on the technical problem of spatial representation building. It seems that priors might not be necessary to capture the different properties of space. Space itself induces specific sensorimotor regularities that can be captured as a by-product of trying to predict future sensorimotor experiences.

These results are very preliminary, as they have only been produced for simple robot-environment systems. Yet they offer a new way to look at the problem of spatial knowledge acquisition. The approach might even extend beyond the single of space. Could other concepts (like objectness, shapeness, color, texture…) also induce specific sensorimotor invariants that could be characterized? Could they be autonomously extracted by a robot which tries to best predict its own sensorimotor experience? A positive answer to those questions would be a giant leap forward towards autonomous robots that would rely only on minimalistic priors to understand their world.