Easily Calculate 0.625 As A Fraction In The Simplest Form

Below we will cover how to calculate 0.625 as a fraction, giving you 5/8 as the simplest form of 0.625.

“In mathematics, the art of asking questions is more valuable than solving problems.” — Georg Cantor

Hence, the simplest form of the fraction derived from the decimal 0.625 is 5/8. How did we get to that number though? Let’s take a close look at deriving fractions from decimals and then expressing those fractions in their simplest form.

Turning Decimals Into Fractions

Photo: Clker-Free-Vector-Images via Pixabay, CC0

Let’s suppose you have a decimal, but what you need is a fraction. Specifically, say that you have the decimal 0.625 and you want to turn it into a fraction. In order to do that, you should know some things about the relationship between decimals and fractions.

Decimals represent a portion of a whole number. The first column after the decimal point is called is tenths place, the second column is the hundreds place, and the third column is the thousandths decimal place. The number 1.10, a one with two decimal places behind it, can be seen as 1 and one-tenth.

Note that the decimals have a close relationship with percents. 1.00 is just 100%, and to get any number behind the decimal point in a percentage, all you have to do is move the decimal point over two places to the right. So 0.12 would become 12%.

As for how one would convert a decimal to a fraction, that’s also very simple. You simply take the decimal and place the corresponding number of columns used underneath it. Let’s say you have the decimal 0.412. The 2 is in the thousandths column, so we could just say that the this is equivalent to 412/1000. (This is also 41.2%.)

Reducing A Fraction To Its Simplest Form

412/1000 is a little unwieldy though. In terms of a fraction, it could be much smaller. How would we go about finding the smallest fraction that could represent the decimal? Finding that smallest fraction called putting the number in its lowest terms, or reducing it. In order to put the fraction in its lowest terms, we need to find something called the Greatest Common Factor (sometimes called the Greatest Common Divisor).

“If I had 60 minutes to solve a problem, I’d spend 55 minutes defining it and 5 minutes solving it.” — Albert Einstein

For the fraction 412/1000, we want to find the largest number that evenly divides into both the numerator and the denominator. In this case, the largest number that goes evenly into both 412 and 1000 is 4. Now, all we have to do is divide both parts of the number by 4. This gives us 103/250.

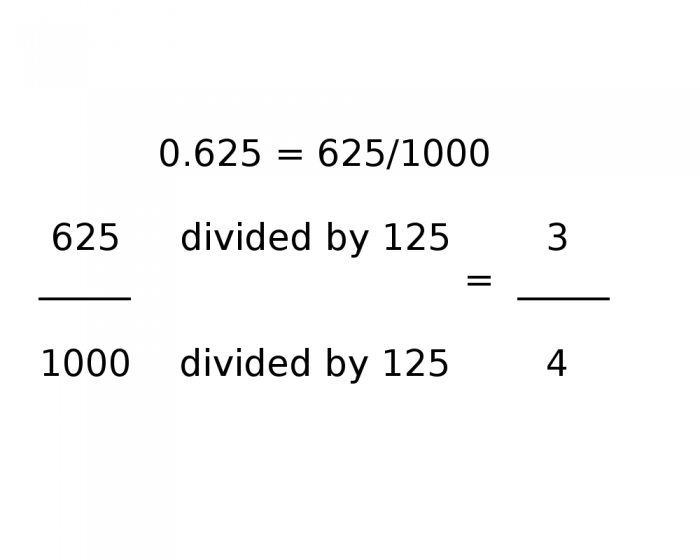
How to calculate 0.625 as a fraction (Photo: My Own)

Getting back to our original example of 0.625, we have to find the Greatest Common Factor for 625/1000. In this case, the number we’re looking for is 125. 125 divides into 625 five times, and it divides into 1000 eight times. This means the simplest form of 625/1000 is ⅝.

In the above examples, we knew the Greatest Common Factor already, but in reality, you’re usually going to have to do some math to find that number. What’s the easiest way to find the GCF? Finding the GCF can be done by listing the primes of each number, and then multiplying out the common prime factors.

Listing the primes:

Let’s take the fraction 18/24 for example. Prime factors are numbers which can only be multiplied by the number one and itself. The prime factors of 18 are two and three, the smallest numbers that can be multiplied to get us 18 (2 x 3 x 3 = 18). Meanwhile, the prime factors of 24 are also 2 and 3 (2 x 2 x 2 x 3 = 24). Multiplying 2 and 3 together gets us 6, which we divide into 18/24. This reduces neatly to ¾.

Let’s take a look at one more example.

Photo: My Own

Let’s find the greatest common factor of 168/210. The prime factors of 168 are 2, 3, and 7 (2 x 2 x 2 x 3 x 7 = 168). The prime factors of 210 are 2, 3, 5, and 7 (2 x 3 x 5 x 7 = 210). Multiplying the common factors – 2, 3, 7 – together gives us 42. Dividing 42 into both the numerator and denominator of 168/210 gives us ⅘.

There are a couple of other ways you could find the greatest common factor. An alternate way to find the GCF is to simply list out all the factors and choose the largest factor the two numbers have in common.

Listing the factors of a number:

For instance, if your fraction is 64/96, listing them out gives you these factors:

Factors for 64 are 1, 2, 4, 5, 16, 32, and 64.
The factors for 96 would end up being: 1, 2, 3, 4, 6, 7, 12, 16, 24, 32, 48, and 96.

Now let’s identify the shared factors: 1, 2, 4, 8, 16, 32.

Now we know that 32 is the greatest common factor, which we can divide into 64/96 to get ⅔.

Dividing a number into smaller chunks:

Yet another method of finding the greatest common factor is the division method. You can divide two numbers into smaller and smaller chunks. Every time the two numbers have common factors divide them until you end up with numbers that can’t be divided anymore. For instance, let’s find the GCF of 144/280.

Photo: My Own

Diving both 280 and 144 by 2 means you get:

140 and 72. 140 and 72 share more common factors between them, so we can divide this further. Let’s try dividing by two again. This gives us:

70 and 36. 70 and 36 still have shared factors between them, so they can be divided further. Let’s divide them by two again:

35 and 18. These two numbers don’t share any common factors besides 1, so we’ll need to stop here. Now we can multiply together the numbers we divided by 2 x 2 x 2 = 8. Divide 8 into 144/280 and we get 18/35.

“Mathematics is not about numbers, equations, computations, or algorithms: it is about understanding.” — William Paul Thurston

Summing Up:

Remember that decimals can easily be turned into fractions. You do this by simply shifting the decimal over to the right until you hit zero, then seeing how many columns you had to move the decimal point over. If the last number is in the thousands column, put 1000 as the denominator.

To put a fraction in its simplest form you want to find the Greatest Common Factor (or the Greatest Common Divisor). There are several different methods of finding the GCF:

You can list the primes of each number and then multiply the common prime factors together. A longer way to do this is to list out all the factors of a number and select the largest factor the two numbers have in common.

You can also keep dividing the numbers by common factors until they no longer have any common factors between them, and are in their simplest form. You’ll then multiply the numbers you divided by together.