Clustering By Shared Subspaces: A New Framework For Data Analysis

Clustering is a fundamental data analysis technique with applications in engineering, medical and biological sciences, social sciences, and economics. For example, clustering could be used to analyze a biological tissue dataset from cancer patients such that certain important cells types can be identified and separated out for further investigation. It could also be used for market research by breaking down market trends and customer habits into meaningful segments according to their shared characteristics.

Many clustering algorithms have been invented over the decades with quite varied properties, but all with the same aim of grouping similar points together and separating out dissimilar points as much as possible.

In the real world though, clusters often exist in different subspaces of a multidimensional dataset. By “existing in a subspace,” we mean that description for the cluster involves only a subset and not all of the dimensions of the data points. Consequently, checking whether a point lies within a certain cluster involves checking the values of only that subset of the dimensions.

For example, imagine clustering stars in the night sky based on measurements of their luminosity, spectral decomposition, angle from the horizon, and timestamp when the image of them was taken. A cluster of a certain type of star, say Red Dwarfs, might be discovered and be distinguished from the other stars by their color and luminosity. Since the property of being a Red Dwarf is not transient, cluster membership should not depend on the angle to the horizon nor the timestamp of the image.

For each subspace cluster, dimensions that are not included in its subspace are considered irrelevant and can be treated as noise. Traditional “full-space clustering” algorithms have difficulty in identifying these clusters since many irrelevant attributes may cause the similarity measurements used by the algorithm to become unreliable.

This observation led to the development of specialized subspace clustering algorithms. Such algorithms can generally be divided into two groups: bottom-up and top-down, based on the direction in which they search for clusters. A bottom-up subspace search strategy starts from one-dimensional subspaces and builds higher dimensional subspaces progressively, whereas a top-down search method determines the subspace of a cluster by starting from the full-dimensional space and iteratively removing irrelevant attributes. Since iterating over all possible subspaces would generate 2^d candidates (where d is the number of distinct attributes), it is impractical for datasets with a reasonable number of dimensions, and thus to avoid having to perform an exhaustive search, the two search strategies utilize some criteria to prune the search space.

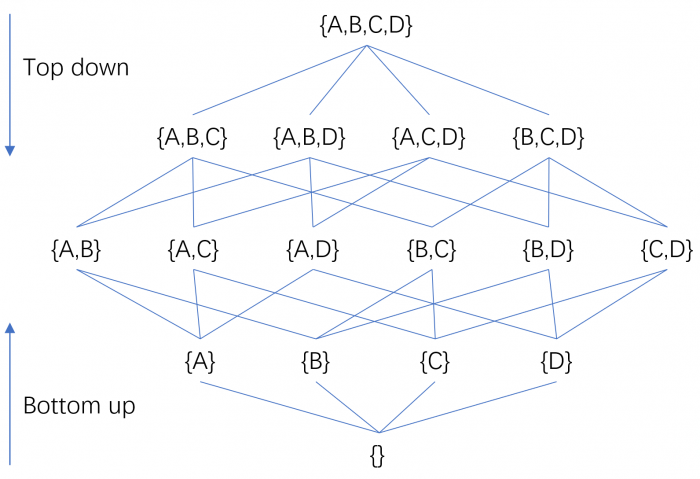
Credit: Ye Zhu

Our study contributed a new subspace clustering framework, which we named CSSub for “Clustering by Shared Subspaces.” The intuition for the work is to turn the normal idea of distance-based clustering upon its head. Instead of measuring the similarity between points based on their relative distance from one another, we measure the similarity based on the number of subspaces they share. But what does it mean to say that two points share a subspace?

To answer that question, we must first discuss another very common clustering technique called density-based clustering. There are many density-based clustering algorithms, with the most famous among them being an algorithm called DBScan. In these algorithms, the density of data around each point is measured – typically by counting points within a certain radius – and then datapoints in high-density regions are linked together to form clusters. Datapoints with low-density values – below a certain threshold – are discarded. In effect, those low-density points are considered unrepresentative of the data overall and treated as noise.

So what does that have to do with points sharing subspaces? Well, if while performing subspace clustering we project our dataset down to a particular subspace – by ignoring all the other dimensions – we can decide whether a point “belongs to the subspace or not” by determining whether it is high enough density in that subspace to not be discarded by a density-based clustering algorithm. Furthermore, we say that two points “share a subspace” if neither of the points is considered noise in that subspace.

Thus, our CSSub framework builds a completely new similarity measure between datapoints that depends on the number of subspaces they share and then uses this similarity measure to cluster the datapoints. This is a fundamentally different approach to subspace clustering since we are now determining the similarity between points based on the mutual agreement on the important subspaces (i.e. those in which the points are not considered noise). The effect of this approach is to explicitly splits candidate subspace selection and clustering into two separate processes, enabling different types of cluster definitions to be employed easily.

The new subspace-clustering procedure works in four stages as follows. In the first stage, it generates an initial set of (relatively) low-dimensional subspaces using strategies such as the bottom-up method. In the second stage, all points in the dataset are labeled as belonging or not to each subspace, based on their density values and – critically – a threshold value that is specific to the subspace and adaptive to the way in which the data is distributed. (The threshold is chosen to maximally characterize clusters within a subspace.) In stage 3, the similarity between pairs of datapoints computed using the Jaccard similarity, i.e. the relative frequency of agreement on “important subspaces,” and an existing clustering algorithm is employed to cluster the points. Finally, in stage 4, certain refinement methods are applied to the clusters, e.g., to find a principle subspace for each cluster.

CSSub decouples the candidate subspace selection process from the clustering process. By explicitly splitting them into independent processes, we eliminate the need to repeat the clustering step a large number of times – namely once for each subspace. (Note that for CSSub to determine which datapoints belong to each subspace, it needs only determine the density around each point in the subspace and not perform clustering over the datapoints. The effect of this approach is to provide a great deal of flexibility in CSSub, allowing for alternative importance measures (other than density thresholds) to be used for determining subspace membership and also alternative clustering methods to be employed for discovering clusters.

Thus, CSSub has the ability to detect non-redundant and non-overlapping subspace clusters directly by running a clustering method only once. In contrast, many existing subspace-clustering algorithms need to run a chosen clustering method for each subspace; this must be repeated for an exponentially large number of subspaces. As a consequence, these methods produce many redundant subspace clusters.

Through an extensive empirical evaluation on synthetic and real-world datasets, we found that CSSub significantly outperforms existing state-of-the-art subspace clustering algorithms for discovering arbitrarily subspace clusters in noisy data. In addition, CSSub has only one parameter k – the number of clusters – which needs to be manually chosen, while other parameters can be automatically set based on a heuristic method.

Like all existing subspace-clustering algorithms, CSSub is designed for low-to-medium dimensionality datasets, since generating all potential subspaces in CSSub results in exponential time complexity with respect to the dimensionality of the original data. Extending CSSub to deal with high-dimensional datasets presents an interesting future work.

These findings are described in the article entitled Grouping Points by Shared Subspaces for Effective Subspace Clustering, recently published in the journal Pattern Recognition. This work was conducted by Ye Zhu from Deakin University, Kai Ming Ting from Federation University, and Mark Carman from Monash University.