
Quantum computers spare no efforts to offer the superior promise of performing complex and unimaginable problems, which are far beyond the reach of any classical computers known at present, in a reasonable time with high accuracy.
The new approach for computing, based on the central principals of quantum mechanics, could have enormous applications, and may revolutionize ubiquitous areas. It could help us discover new medicines and materials. It could change how we invest by remodeling financial services, managing money as well as massive datasets. It could lead to great advances in artificial intelligence, optimization, and machine learning. It may facilitate finding optimum solutions for supply chains and logistics, it could increase the efficiency of parallel computations, create secure network applications, simulate molecular structures, break unbreakable codes, or even crack cryptography and encryption. This would potentially lead to enable future technologies [1,2].
The assiduous potential of quantum computation could make it be the best solution ever to overcome the conceivable limits that confront human beings in several fields. Its impacts are apparently endless.
A quantum computer is a completely distinct concept; it doesn’t depend on binary logic, it depends on what is called quantum bits or qubits. Basically, the huge advantage of qubits over normal bits is that they exist in a superposition of states; thus, whereas a standard bit may be either a one or a zero, a qubit may be a one, a zero, or both a one and zero at the same time. If we have a maze, a binary computer has got to take the time to separately assess each path. Quantum computers would assess every possibility at the same time.
The most popular method of quantum computation and communication is gate-based. Quantum gates are employed to handle and transform information under the laws of quantum mechanics. It takes a qubit and transforms it into a new state. Quantum gates are the building blocks of quantum computers, like classical logic gates for conventional computers. They generally act on a superposition of quantum states. A series of finite numbers of such gates could construct quantum algorithms, procedures for performing computations in quantum systems. The obstacle of constructing a quantum computer is equivalent to finding a physical implementation of quantum gates between qubits [3-5]. They provide fundamental building blocks for encoding complex algorithms and operations [6].
Many physical schemes [7-14] have been proposed for building quantum bits. The finest success of any such proposal depends on the level to which the physical scheme can be designed to fulfill the requirements to build a quantum computer, known as the DiVincenzo criteria [15]. Satisfying any of these requirements individually can be accomplished easily. However, satisfying all DiVincenzo requirements together is challenging and at the frontier of recent research in quantum computation [14].
Since its creation a hundred years ago, quantum mechanics has had something unexpected to offer nearly every single year. The last few decades, in particular, have seen a dramatic increase in theoretical and practical advances. But the foremost exciting developments in quantum mechanics are for certain those related to building genuine quantum computers with computational powers transcending any conventional computer.
In November 2017, however, IBM announced a 50-qubit quantum computer [16], and we may reach a 100-qubit quantum computer soon. Quantum computers are hard to build and harder to maintain. They are extremely fragile and need huge amounts of infrastructure just to function. Although the technology is here [17-20], there are several barriers to full-scale implementation.
Conditional necessities such as the need to handle physical concerns, as processors need to be kept at near-perfect-zero temperatures within hundredths of a degree, means the hardware must reside in a laboratory, such as the IBM labs. Also, one of the biggest limitations is the decoherence problem. It’s so acknowledged that no system, in reality, is perfectly isolated. Decoherence can be considered as the loss of quantum information from a system into the environment. Quantum states are subtle objects; sneeze, and they vanish.
Last, but not least, is the hope to reach what J. Preskill referred to as “quantum supremacy,” the position when a quantum computer is able to process a task otherwise thought impossible [21-24]. Quantum computation is meaningless if it not advanced to handle all the noise generated by qubits.
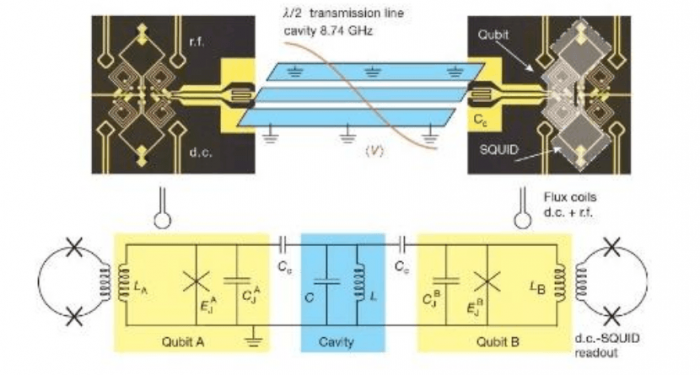
Fig. 1 Schematic description of the experiment [25]. The interaction circuit is composed of two Josephson phase qubits connected via coupling capacitors to either end of a resonant cavity. Reprinted with permission under license number: 4114230456888. Nature Publishing Group.
A principal cause of decoherence in superconducting qubits is relaxation and dephasing [30] in open quantum systems;, each implementation scheme is distinguished by its own relaxation and dephasing times. Accordingly, we have to implement our computations in time less than these times.
The physical model used through our investigations composed of three directly coupled superconducting quantum systems, two superconducting phase qubits and one resonant cavity [31], as shown in figure (1), to investigate the influence of the photon number present in the cavity, as a parameter of control, and its influence on their implementation times of quantum algorithms.
AbuGhanem et. al. in [32] propose and analyze a new approach with a detailed experimental procedure to explore the influence of the number of photons in the cavity on the realization times of one- and two-qubit quantum gates in order to realize the quantum algorithms for circuit QED.
The study demonstrates the contextual use of the photon number as a good parameter of control on the realization times of any quantum algorithm. It is shown that the required times to realize the quantum algorithms depend on the number of photons in the resonant cavity. In a sense that whenever the photon numbers slightly increase over the qubits number, the realization times accordingly decrease.
Our findings lead to a better understanding of the properties of such systems from which multi-qubit algorithms can be realized. In addition, the time for implementing the protocol using the proposed technique is compared with different previous schemes.
Results indicate the possibility of full integration into the realization of multi-qubit multiphoton states to design quantum algorithms. This constitutes as direct evidence that multi-qubit algorithms can be realized in systems in which the photon number is increased slightly over the qubits number. Such algorithms can be implemented in considerably less time than the dephasing and relaxation times of the system.
Hopefully, our results pave the way toward the full integration of multi-qubit multiphoton states. Furthermore, the technique that originated from this research may be used in other, perhaps more scalable, quantum computer implementations in future experiments.
These findings are described in the article entitled Cavity control as a new quantum algorithms implementation treatment, recently published in the journal Frontiers of Physics.
References:
- U. Alvarez-Rodriguez, M. Sanz, L. Lamata & E. Solano, Quantum Artificial Life in an IBM Quantum Computer , Scientific Reports volume 8, Article number: 14793 (2018).
- Applications of quantum computing, IBM https://www.ibm.com/quantum-computing/
- C. Monroe, D. M. Meekhof, B. E. King, W. M. Itano, and D. J. Wineland, “ Demonstration of a fundamental quantum logic gate,” Phys. Rev. Lett., vol. 75, no. 4714, 1995.
- R.W. Simmonds, K. Lang, D. Hite, S. Nam, D. Pappas, and J. Martinis, “ Decoherence in Josephson phase qubits from junction resonators ,” Phys. Rev. lett., vol. 93, no. 7, p. 077003, 2004.
- T. Sleator and H.Weinfrter, “ Realizable universal quantum logic gates,” Phys. Rev. Lett., vol. 74, p. 4087, 1995.
- Isaac Chuang, Building the building blocks, Nature Physics volume 14, pages974–975 (2018)
- E. Fredkin and T. Toffoli, “ Conservative logic ,” Int. J. Theor. Phys., vol. 21, no. 3-4, pp. 219–253, 1982.
- D. P. DiVincenzo, “ Quantum computation ,” Science, vol. 270, no. 5234, pp. 255–261, 1995.
- B. Kane, “ A silicon-based nuclear spin quantum computer,” Nature, vol. 393, no. 6681, pp. 133–137, 1998.
- N. Gershenfeld and I. L. Chuang, “ Bulk spin resonance quantum computation,” Science, vol. 275, no. 5298, pp. 350–356, 1997.
- D. G. Cory, A. F. Fahmy, and T. F. Havel, “ Ensemble quantum computing by NMR spectroscopy,” Proc. Nat. Acad. Sci., vol. 94, no. 5, pp. 1634–1639, 1997.
- Y. Nakamura, Y. A. Pashkin, and J. S. Tsai, “ Coherent control of macroscopic quantum states in a single-Cooper-pair box,” Nature, vol. 398, pp. 786–788, 1999.
- P. M. Platzman and M. I. Dykman, “ Quantum computing with electrons floating on liquid helium,” Science, vol. 284, no. 5422, pp. 1967–1969, 1999.
- M. Steffen, D. P. DiVincenzo, J. M. Chow, T. N. Theis, and M. Ketchen,“ Quantum computing: An IBM perspective,” IBM J. RES. & DEV., vol. 55, p. 5, 2011.
- D. P. DiVincenzo, “ The physical implementation of quantum computation,” Fortschr. Phys., vol. 48, no. 9-11, pp. 771–783, 2000.um
- IBM builds 50-qubit quantum computer. http://techvibesnow.com/ibm-builds-50-qubit-quantum-computer/, November 2017. computing
- Rigetti computing, Quantum Cloud Services , https://www.rigetti.com
- IBM Q, The future is quantum, https://www.ibm.com/quantum-computing/
- Google AI, https://research.google/teams/applied-science/quantum/
- Martinis Group, Josehson Junction Quntum computing at UCSB, https://web.physics.ucsb.edu/~martinisgroup/index.shtml
- J. Preskill. Quantum computing and the entanglement frontier. In H. M. Gross, D. and A. Sevrin, editors, The Theory of the Quantum World, pages 63–80, Singapore, November 10 2012. World Scientific Publishing. arXiv:1203.5813 [quant-ph].
- C. Neill et.al., A Blueprint for Demonstrating Quantum Supremacy with Superconducting Qubits, Ref: arxiv.org/abs/1709.06678, (2017)
- S. Boixo, S. V. Isakov, V. N. Smelyanskiy, R. Babbush, N. Ding, Z. Jiang, M. J. Bremner, J. M. Martinis, and H. Neven. Characterizing quantum supremacy in near-term devices. arXiv:1608.00263 [quant-ph], April 2017.
- Cristian S. Calude, Elena Calude, The Road to Quantum Computational Supremacy arXiv:1712.01356v3, 2019.
- M. A. Sillanpää, J. I. Park, and R. W. Simmonds, Coherent quantum state storage and transfer between two phase qubits via a resonant cavity, Nature 449, 438 (2007).
- R. J. Schoelkopf and S. M. Girvin, “Wiring up quantum systems,” Nature 451, 664– 669 (2008).
- S. Haroche and J.-M. Raimond, Exploring the Quantum: Atoms, Cavities, and Photons. Oxford University Press, USA, Oct., 2006.
- H. Walther, B. T. H. Varcoe, B.-G. Englert, and T. Becker, “Cavity quantum electrodynamics,” Reports on Progress in Physics 69, 1325–1382 (2006).
- Lev Samuel Bishop , Circuit Quantum Electrodynamics, PhD Dissertation , Yale University May 2010
- Peter James Joyce O’Malley, Superconducting Qubits: Dephasing and Quantum Chemistry, PhD thesis, UNIVERSITY of CALIFORNIA Santa Barbara, 2016.
- F. Altomare, K. C. J. I. Park, M. A. Sillanpaa, M. S. Allman, D. Li, A. Sirois, J. A. Strong, J. D. Whittaker, and R. W. Simmonds, “ Tripartite interactions between two phase qubits and a resonant cavity,” Nature Physics, vol. 6, pp. 777–781, 2010.
- M. AbuGhanem, A. Homid, and M. Abdel-Aty, Cavity control as a new quantum algorithms implementation treatment, Front. Phys., vol. 13, no. 1, p. 130303, (2018).









