
The idea of molecular structure is fundamental to our understanding of chemistry. While the familiar ball-and-stick model is both concrete and appealing in its simplicity, it is also limiting, or worse misleading, in terms of explanatory value. The notion of the chemical bond as simply a line, or a rod, connecting two atomic symbols, or physical atoms, is one such misleading consequence.
The structure of a given compound is most often determined by x-ray crystallography, where the scattering of photons by the electron cloud surrounding the atom creates a diffraction pattern that in turn reveals the atomic positions. But while the experimental electron density (ρe) yields a molecular structure it does not dictate a specific shape for the molecule, i.e. the density of electrons alone does not uniquely describe the existence of specific bonds connecting the atoms. Molecular structures, such as that shown in Fig. 1, reflect interatomic connections based on proximity and the normal rules of chemical valence. And while characteristics such as bond strength can be inferred, more fundamental properties such as orbital composition are not accessible.
The wave function (ψ) is the fundamental concept in quantum mechanics (QM), and represents, in theory, a complete description of a given molecule. The wave function represents a probability amplitude, with ψ2 giving the probability density for particles at a specific location. Solving the Schrodinger equation for a given molecule involves generating the electronic wave function for a given nuclear configuration (the Born-Oppenheimer approximation) and independently optimizing the nuclear coordinates before calculating an electroniv ψ for the optimized structure. The surface boundary within which there is a 90% probability of finding a given electron is defined as an orbital, and reflects the composition of either localized, two-center, or delocalized, multi-center, bonds. The quality of the QM calculation can be assessed by comparison with the experimental structure, normally determined by x-ray or neutron diffraction. Thus the characteristics of a given bond, i.e. its orbital composition, is obtained from theory rather than from the experimental structure.
In a recent paper the author has been able to demonstrate that there is indeed a relationship between ρe and ψ, namely the equivalence shown in Equation 1 below.
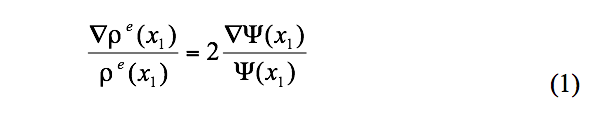 The wavefunction ψ(x1) in (1) is termed a one-electron wavefunction, an approximation to the more rigorous all-electron ψ of the Schrodinger equation. Nevertheless, the utility of the relationship in (1) is that one can use the experimental electron density, ρe, to visualize an experimental version of ψ. Specifically a plot of the experimentally derived
The wavefunction ψ(x1) in (1) is termed a one-electron wavefunction, an approximation to the more rigorous all-electron ψ of the Schrodinger equation. Nevertheless, the utility of the relationship in (1) is that one can use the experimental electron density, ρe, to visualize an experimental version of ψ. Specifically a plot of the experimentally derived
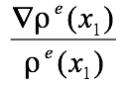
will display topology or spatial arrangement of the one-electron wave function ψ(x1). For the molecule [(C5Me5)OsH4(PCy3)][BF4] Figure 1 shows such a plot, the experimental structure determined by neutron diffraction, and the theoretical description for such interactions, known as the Dewar-Chatt-Duncanson model. Despite the fact that the “experimental” structure indicates near-equivalent bonds between the central metal atom and all four hydrogens, the plotted experimental version of ψ(x1), or ρe(x1), indicates a different bonding interaction between the metal and Ha and Hb, than that observed between the metal and H1 and H2. While differing from the traditional, more localized picture of bonding, the plot is markedly similar to the model predicted by QM theory. For the molecule [FeH3(PMe3)4][BPh4] shown in Figure 2.
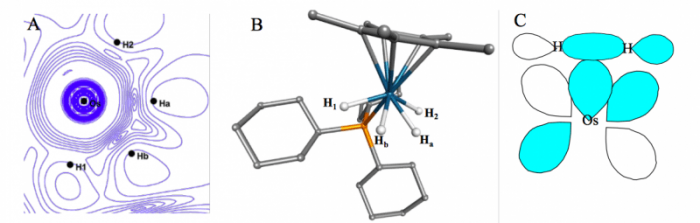
Figure 1 A: the |∇ρe|/ρe isocontour plot in the Os-Hydrogen plane of [(C5Me5)OsH4(PCy3)][BF4]; B: the structure of [(C5Me5)OsH4(PCy3)][BF4] as determined by neutron diffraction; C: the molecular orbital description of metal-H2 bonding as explained by the Dewar-Chatt-Duncanson model. (Credit: Eamonn F. Healy)
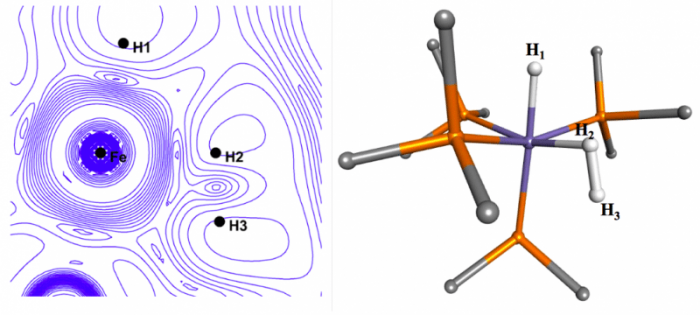
Figure 2 the |∇ρe|/ρe isocontour plot in the Fe-H2 plane and the x-ray structure for [FeH3(PMe3)4][BPh4]. (Credit: Eamonn F. Healy)
The formalism known as the Quantum Theory of Atoms in Molecules (QTAIM) is based on retrieving the idea of the localized chemical bond through analysis of a molecule’s electron density, and part of the chemistry Nobel prize in 1998 was awarded for the development of Density Functional theory (DFT), a solution to the Schrodinger equation based on ρe rather than ψ as the fundamental variable. However. this work links the experimental ρe with the theoretical ψ in a way that is at once visual, widely applicable, and hopefully useful.
These findings are described in the article entitled Visualizing the molecular wave function in σ−coordinated complexes, recently published in the journal Computational and Theoretical Chemistry. This work was conducted by Eamonn F. Healy from St. Edward’s University.
References:
- Healy, Eamonn F. “Visualizing the molecular wave function in σ−coordinated complexes”, Computational and Theoretical Chemistry, 1125 (2018) 128-132.
- Hunter, Geoffrey. “Conditional probability amplitudes in wave mechanics.” Int. J. Quantum Chem 9 (1975) 237-242.
- Gross, Christopher L., and Gregory S. Girolami. “Synthesis and NMR Studies of [(C5Me5) Os (L) H2 (H2)+] Complexes. Evidence of the Adoption of Different Structures by a Dihydrogen Complex in Solution and the Solid State.” Organometallics 26 (2007): 1658-1664.
- Gusev, Dmitry G., et al. “Synthesis, Structural Diversity, Dynamics, and Acidity of the M (II) and M (IV) Complexes [MH3 (PR3) 4]+(M= Fe, Ru, Os; R= Me, Et).” J. Am. Chem. Soc.119 (1997) 3716-3731.
- Mingos, D. Michael P. “A historical perspective on Dewar’s landmark contribution to organometallic chemistry.” J. Organomet. Chem. 635 (2001) 1-8.
- Bader, Richard FW. “Atoms in molecules.” Accs. Chem. Res. 18 (1985) 9-15.









