The Dynamical Behaviors In The Rotating Plane-Symmetric Potential Field

The rotating plane-symmetric potential field is an approximation of gravitational field for several different celestial bodies in the Solar system, including the circular restricted three-body problem, planetary ring’s gravitational environment, asteroids 4 Vesta, 1620 Geographos, etc. 

There are several synchronous binary asteroids found in the Solar system, including 809 Lundia, 1089 Tama, etc. The two components of the synchronous binary asteroids are locked to each other, which means the primary and the secondary always take the same surface facing each other. Thus, the rotating plane-symmetric potential field is also an approximation of the gravitational field for synchronous binary asteroids.

Studying the dynamical behaviors of spacecraft and grains in these celestial bodies is useful for future space missions and understanding the evolution of grains. It is found that the dynamical behaviors in the z-axis are independent relative to the dynamical behaviors in the xy plane. During the variety of parameters, the local dynamical behaviors at the resonant equilibrium point which is non-degenerate will change, and the Hopf bifurcation occurs.

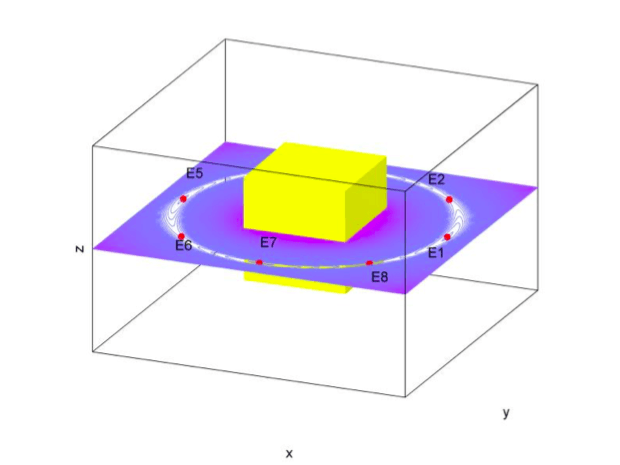
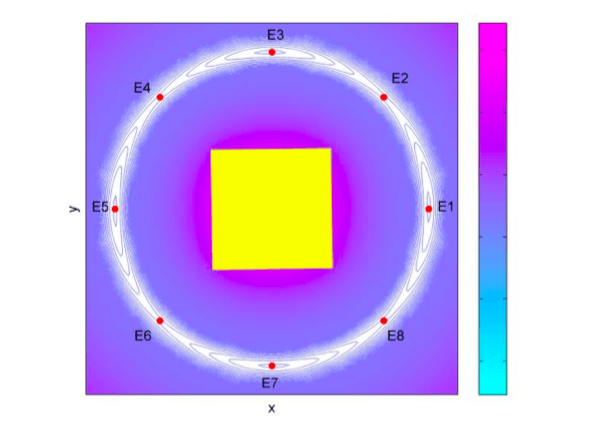
Fig. 1: Equilibrium points in the gravitational field of a rotating cube. Images courtesy Yu Jiang

The theory is applied to study the relative equilibria of a rotating homogeneous cube and the asteroid 1620 Geographos. The gravitational field of this asteroid is nearly plane-symmetric. Due to the YORP effect, the rotation speed of asteroid 1620 Geographos is increasing with an angular acceleration of 0.000481deg·year^-2. The YORP effect is caused by the interaction of electromagnetic radiation and the surface of asteroids, which can change the rotation state of asteroids. Now the rotational period of asteroid 1620 Geographos is 5.222hour. Steroid 1620 Geographos has five equilibrium points at present. However, the number of asteroid 1620 Geographos may change during the variety of the rotational speed. 

Suppose the angular acceleration is a constant. Then, after about 3.26 million years, two equilibrium points of asteroid 1620 Geographos collide and annihilate each other. After about 9.12 million years, another two equilibrium points of asteroid 1620 Geographos will also collide and annihilate each other. That is to say, after about 3.26 million years, asteroid 1620 Geographos will have only three equilibrium points. After 9.12 million years, asteroid 1620 Geographos will have only one equilibrium point left.

The two positions of collision are inside the body of the asteroid. Before the external equilibrium point moves inside the asteroid, the external equilibrium point will touch the surface of the asteroid. Once the external equilibrium point touches the surface, the surface shedding occurs. If the surface of the asteroid is loose, the surface will change during the acceleration process of the asteroid. If the structure of the asteroid is loose, the asteroid will break up before the second collision of equilibrium points.

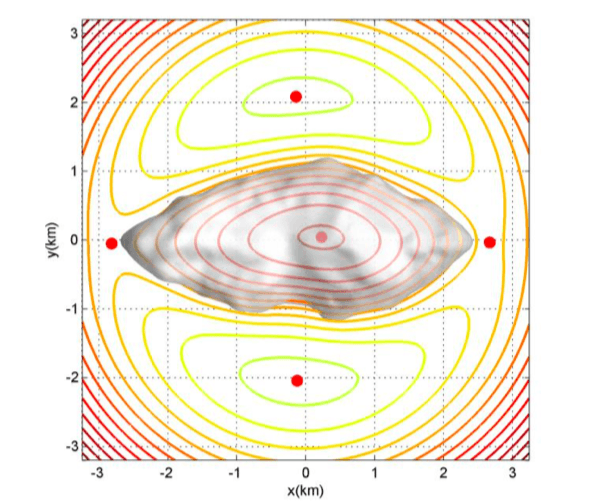
Fig. 2: Equilibrium points in the gravitational field of asteroid 1620 Geographos. Image courtesy Yu Jiang

Fig. 3: Equilibrium points in the gravitational field of asteroid 1620 Geographos after about 3.26 million years with the angular acceleration of 0.000481deg·year-2. Image courtesy Yu Jiang

These findings are described in the article entitled Stability and motion around equilibrium points in the rotating plane-symmetric potential field, recently published in the journal Results in Physics. This work was conducted by Yu Jiang, Hexi Baoyin, Xianyu Wang, and Hengnian Li from Tsinghua University and Xi’an Satellite Control Center.