Prime Numbers And Crystal-Like Materials Share A Hidden Organization

As it turns out, prime numbers and crystals have a lot in common. A new analysis from researchers at Princeton University suggests that the patterned distribution of prime numbers in the number line is remarkably similar to patterns found in the atomic structure of certain crystal-like materials.  In simple terms, the sequence of primes over long stretches of the number line shows properties remarkably similar to the sequence that arises from shining X-rays on an object to reveal its internal atomic structure.

The study, published in The Journal of Statistical Mechanics, shows that the organization of primes bears a striking similarity to the atomic organization found in quasicrystals — strange crystal-like materials with an aperiodic atomic organization. Both the organization of prime numbers and that of quasicrystals fall under a class of patterns known as “hyperuniform.” The potential applications of this knowledge are exciting. Mathematicians have long sought for an algorithm that could predict the location of prime numbers in the number line, but no such algorithm has been found yet.

“Some numbers, even large ones, have no factors – except themselves, of course, and 1. These are called prime numbers, because everything they are starts with themselves. They are original, gnarled, unpredictable, the freaks of the number world.” — Richard Friedberg

According to the researchers, the knowledge gained from the study could help to devise new methods for predicting primes on the number line. Said Salvatore Torquato, lead researcher on the study, “There is much more order in prime numbers than ever previously discovered,”

Prime Numbers, Quasicrystals, And Hyperuniformity 

Prime numbers are numbers whose only factors are one and themselves; numbers like 3, 7, 11, or 2^74,207,281−1. Very large prime numbers are the building blocks of modern cryptography. Prime numbers seem to be more or less randomly distributed across the number line. Currently, there exists no algorithm for generating primes but mathematicians have been able to determine some extremely general features about their organization. The further on the number line you go the more prime numbers are spread out. also, the chance of a randomly selected number being a prime number is inversely proportional to the number of digits in that number.

Torquato, a professionally trained chemist, is familiar with X-ray crystallography, the process of shining X-rays through an object to map its atomic structure in 3 dimensions. For ordered and periodic crystals, like diamonds or quartz, crystallography results in a predictable pattern of bright spots, known as Bragg peaks. Quasicrystals lack the periodic structure of regular crystals and so compared to regular crystals, quasicrystals exhibit a distinct and complex pattern of Bragg peaks.

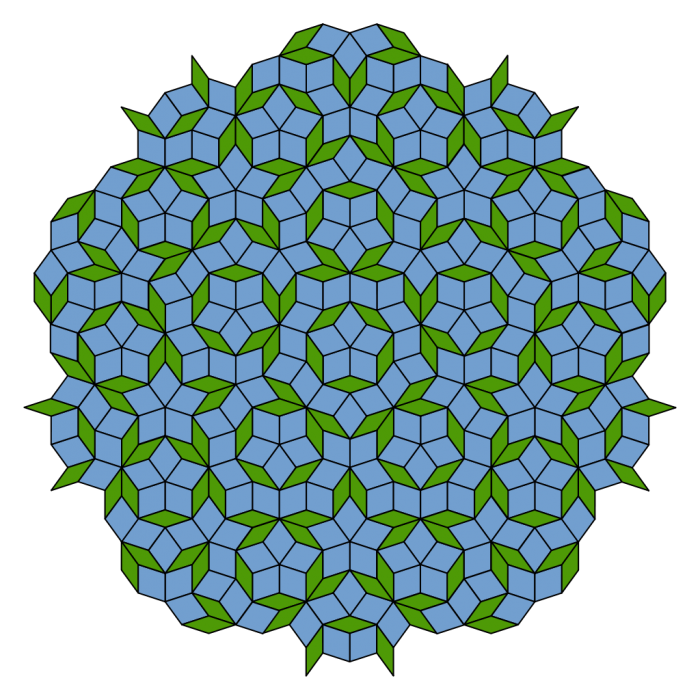
A Penrose tiling, an example of a quasicrystal arrangement. Source: Wikipedia, licensed under CC0

In a previous study published in February, the team used powerful computer simulations to show what would occur if prime numbers were treated like atoms arranged in a lattice subjected to X-rays. The results showed that the prime-ordered crystals showed a Bragg peak pattern very similar to that of a quasicrystal, and another kind of system called “limit periodic order.” The current paper is intended to offer a theoretical explanation for the numerical results of the previous experiment.

All of these organizations fall under a class of patterns known as “hyperuniform” materials. A hyperuniform material (sometimes called “superhomogenous”) is one that appears to show no obvious order but takes on a special organizational structure at large scales. Although it may sound contradictory, one could say a hyperuniform material is one of “ordered chaos” — the pieces seem randomly arranged at small scales, but there is an order to the madness from a bird’s eye view.

Since the genesis of the concept of hyperuniformity in the early 2000s, hyperuniform patterns of organization have been found all over nature, including in the eyes of chickens, quasicrystals, distributions of random numbers, quantum ensembles of particles, and even the large-scale structure of the universe. Like the Fibonacci sequence, mathematical patterns of hyperuniformity are found all over nature, and their unexpected discovery almost always takes scientists by surprise.

In this case, the pattern that Torquato and cohorts found in prime numbers is similar to that in quasicrystals and other systems of limit period order, but different enough that they gave it the name “effectively limit order.” The primes appear in “self-similar” groupings, meaning that between peaks of equal height there are groupings of smaller peaks.

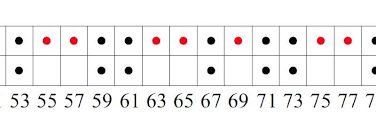
Here red dots are non-prime numbers while black dots are prime, which are treated like “atoms.” Source: Torquato, S.; et. al. (2018) “Uncovering Multiscale Order in the Prime Numbers via Scattering” Journal of Statistical Mechanics: Theory and Experiment <https://doi.org/10.1088/1742-5468/aad6be>

Links to Mathematics

All this is to say that the study suggests that the same mathematical rules underly both the distribution of primes in the number line and the 3-dimensional atomic structure of certain materials. It is often the case that mathematical concepts refined in one domain are surprisingly found to be applicable in another domain. It was certainly a surprise for early 20th century physicists when they discovered that non-Euclidean geometries, at the time just an interesting mathematical curiosity, were applicable as models of general relativity. Likewise, the early pioneers of quantum mechanics were surprised when it turned out that matrix algebra actually had an application in early quantum theory. Once again, we see a particular mathematical concept, that of hyperuniformity, rear its head in two seemingly unrelated domains — material sciences and number theory.

The results of Torquato and his colleagues’ analysis is exciting for the scientific community. According to Henry Cohn, a researcher at Microsoft who was not involved with the study, “What’s fascinating about this paper is that it gives us a different perspective on the primes: instead of viewing them as numbers, we can view them as particles and try to map out their structure via X-ray diffraction.”

It is thought the new information could go lengths to creating algorithms to generate prime numbers, which could change the entire face of mathematics as we know it.

In a way, the new study somewhat inverts the traditional understanding of the relationship between mathematics and science. Generally, scientists use mathematics to make predictions about the physical world, but now it seems that we might be able to use the physical world to make predictions about mathematics! Galileo Galilei is often credited with saying that the book of the universe is written in the language of mathematics and its characters are triangles, circles, and other geometric figures. It seems that this lesson rings true, even 400 years later.