Internal Gravity And Binding Energy Of Comets And Asteroids

The gravitational field outside a planet, a moon, an asteroid, or a comet is crucial for determining that body’s mass, density, and some details of its internal structure, as well as possible orbits around that object. But the gravitational field inside such a body controls its internal stresses and strains, as well as its self-gravitational binding energy.

The latter is important for determining the energy of a collision which can disperse that object into tiny fragments, a vital quantity for understanding the origin and evolution of small bodies, such as comets and asteroids.

Most asteroids are shaped like potatoes, but most comets seem to be shaped more like peanuts, with two lobes; so while comets are often described as “dirty snowballs,” they may be characterized better as “dirty snowmen.” Because small bodies usually are irregular in shape, they often are modeled as polyhedra with thousands of faces, while the corresponding gravitational fields are given by complicated analytical formulae. These formulae apply equally well inside the polyhedron as outside it, although this fact is not generally well-known.

A recent study (1) uses these formulae numerically to find the gravitational fields inside a variety of homogeneous objects, including the five classical Platonic solids (regular tetrahedron, cube, octahedron, dodecahedron, and icosahedron), as well as much more complicated models of the ham-bone-shaped asteroid (216) Kleopatra and the bilobate comet 67P/Churyumov-Gerasimenko (see Fig. 1). These internal gravities are then used to determine the self-binding energy of each body.

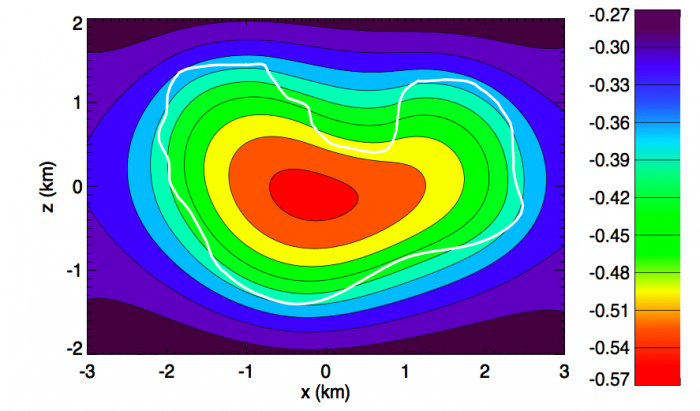
Figure 1: The geopotential field U in the xz plane of comet 67P/Churyumov- Gerasimenko. The white outline shows the intersection of the comet’s surface with this plane. The origin lies at the center of mass of 67P, while the x-axis lies along its axis of least inertia, and the z-axis lies along its axis of greatest inertia (spin axis). The scale bar is in Joules per kilogram. As on Earth, the geopotential U is the sum of the pure gravitational potential and the centrifugal potential (both negative), here corresponding to 67P’s rotation period of 12.40 hours. The gradient of −U gives the effective gravity (the pure gravitational acceleration plus the centrifugal acceleration), while the integral of −U over the volume of the comet (multiplied by its density of 540 kg/m3) gives its net binding energy. Adapted by Don Korycansky from Figure 5 of paper (1).

For example, the self-gravitational energy of comet 67P/C-G amounts to 2.21 ×1012 Joules, compared to 2.43 ×1012 Joules for a homogeneous sphere of the same mass and density. However, 67P already has a rotational kinetic energy of 0.19 ×1012 Joules, so its net binding energy comes to only some 2.02 ×1012 Joules. Thus, both the irregular shape and the spin of an object reduce its net binding energy.

Paper (1) also relates this binding energy to the collisional energy needed to disrupt comets, asteroids, and moons. The technique is easily generalized to non- homogeneous bodies; for example, if the two lobes of comet 67P/C-G had different densities. Internal gravity also is relevant to the settling and sifting of dust and fines through cracks and pores and to the percolation of water or other internal melts.

These findings are described in the article entitled Internal gravity, self-energy, and disruption of comets and asteroids, recently published in the journal Icarus. This work was conducted by Anthony R. Dobrovolskis from the SETI Institute, NASA Ames Research Center, and D.G. Korycansky from the University of California, Santa Cruz.