How Asteroid Families Interact With Secular Resonances

Large asteroid families are usually the product of a collision between two bodies. Fragments of the parent body are ejected with terminal ejection velocities that are of the order of its escape velocity, which is usually only a small fraction of the orbital speed of the parent body. As a consequence, the fragments will end up in orbits that are not too dissimilar from that of the parent body.

When proper elements are obtained by removing the short-period effects of the perturbations from the planets, asteroid families will be visible in domains of proper elements, such as the proper semi-major axis a, the proper eccentricity e, and the proper inclination i, where the proper semi-major axis yields a measure of the distance of the orbit pericenter from its center, the eccentricity inform on how an orbit is flat (would be 0 for a circle and 1 for a parabola, with values in between for ellipsis), and the inclination is the angle between the orbital plane and a plane of reference, such as the orbital plane of the Earth.

After the family formation event, the fragments orbits evolve in space because of gravitational and non-gravitational effects. Estimating both the age and initial ejection velocity field of asteroid families is, therefore, not an easy task. Additional information, however, is available for families that interact with secular resonances.

Secular resonances involve commensurabilities between the periods of the precession of the longitudes of the pericenter or of the node of an asteroid and a planet. These angles identify the position with respect to a reference, like the equinoctial vernal point, of the pericenter of the orbit and of the ascending node, i.e., the point where the orbital plane crosses the reference plane and the asteroids goes upward in its motion.

Because of the effect of planetary perturbations, these angles are not fixed in time but precess. When the precession frequency of the longitude of the pericenter g or of the longitude of the node s of an asteroid is equal to that of a planet, a linear secular resonance occurs. The most important linear secular resonances in asteroid dynamics occur when ν₆ =g-g₆ =0 arcsec/yr, ν₅ =g-g₅ =0 arcsec/yr, and ν₁₆ =s-s₆ =0 arcsec/yr. g-type resonances can change an asteroid eccentricity, while s-type resonances affect the body inclination. Non-linear secular resonances involve higher order commensurabilities, like for the z_k = k(g-g₆) +s-s₆ resonances series that involve combinations of both the g and s frequencies.

Secular resonance have a complicated tridimensional topology in the (a,e,sin(i)) domain. Their position on a bidimensional plane depends on the value of the third parameter, as shown in figure 1. The position and dynamical importance of secular resonances can be better assessed in domains of proper frequencies. For instance, (g+s)-type secular resonances, as the z₁, can be better displayed in a (g,g+s) plane, as shown in figure 2.

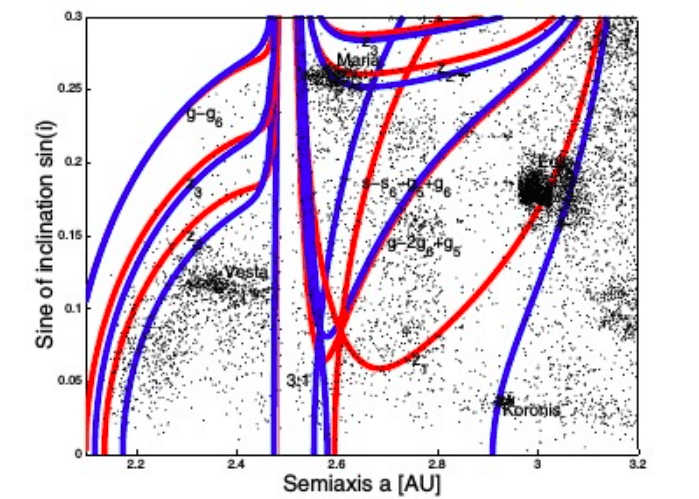
Fig. 1 Location of some of the main secular resonances in the asteroid belt. The secular resonances obtained for the fixed value 0.10 of the proper eccentricity are superimposed to the proper elements a and sin(i) of the asteroids with proper e within the range of ±0.025 of the central value. The names indicate the main asteroid families in the region. The pairs of red and blue lines display the locations of the edges of the resonances. Image published with permission from Elsevier from https://doi.org/10.1016/j.pss.2018.03.009

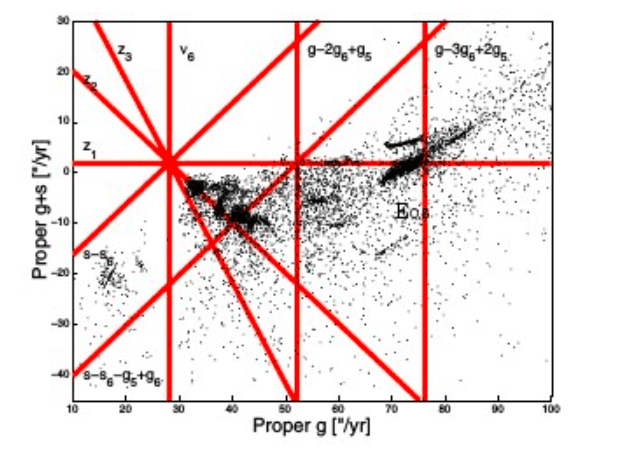
Fig. 2. A projection of asteroids in the (g,g+s) domain.  The horizontal line displays the location of the z1 = g-g6+s-s6 secular resonance. Image published with permission from Elsevier from https://doi.org/10.1016/j.pss.2018.03.009

The ν₆ resonance is one of the main effective mechanisms for increasing an asteroid eccentricity and one of the main sources of Near Earth Asteroids (NEAs). This resonance interacts with the Tina and Euphrosyne asteroid families and sets the boundary to define the region inhabited by highly inclined asteroids in the central and outer main belt. The resonance topology depends on the distance of the asteroid with respect to Saturn. Generally speaking, two main classes of orbital behavior are possible when approaching the resonant configuration. For objects not in resonance, the resonant argument σ will circulate over a full period around the equilibrium point of zero. For orbits in a resonant configuration, the resonant argument will oscillate around the equilibrium point and only cover a limited range of values (see Fig. 3, left panel).

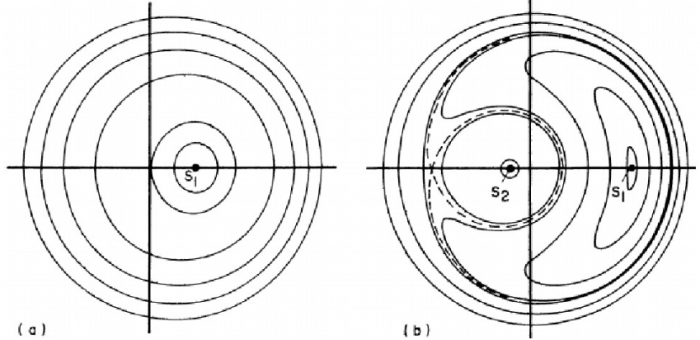
Fig. 3. The phase space in the (ecosσ,esinσ) domain of a first-order resonance far (panel a) and near (panel b) the perturbing objects. Image published with permission from Elsevier from https://doi.org/10.1016/j.pss.2018.03.009

The line dividing these two kinds of orbits is called separatrix. In the central and outer main belt, nearer to the perturbing body, Saturn, a new equilibrium point appears at 180⁰, and the separatrix forms a loop with itself, creating a new class of orbits whose resonant argument oscillates around the new equilibrium point. Since changes in eccentricity are limited within this region, this orbital configuration protects asteroids within from reaching planetary-crossing orbits, so forming a stable island. The Tina family is the only asteroid family whose members are all in anti-aligned states of the ν₆ secular resonance.

There are, however, also families interacting with non-linear secular resonances of the zk series. More than 75% of the members of the Agnia and Padua families are on librating states of the z₁=g-g₆+s-s₆ resonance. 14% of the members of the Erigone family are in librating states of the z₂=2(g-g₆)+s-s₆ resonance. Because of their resonant configuration, the combination of the proper eccentricity and inclination of asteroids in the z₁ resonance given by formula will be preserved after the family forming event, and this can be used to set constraints on the initial ejection velocity field of the Agnia and Padua families. Assuming that the current population of z₂ liberators of the Erigone family is in steady-state, we can also use this information to set lower limits on this family age. The Erigone family should be at least 90 Myr old, based on this argument.

An important recent discovery in the field was that dwarf planets and massive asteroids may also play a role in secular dynamics. Recently, it was found that the linear node resonance with Ceres (ν_1C =s-s_C) affected the dynamical evolution of the Astrid, Hoffmeister, and other asteroid families. They can explain why methods for identifying asteroid family based on a search of neighbors pairs cannot reveal the possible existence of a Ceres family. Secular dynamics with massive bodies can provide constraints on the ages of the “v_W leptokurtic families.” The change in inclination of family members is related to the perpendicular  component of the velocity at infinity v_W through the third Gauss equation:

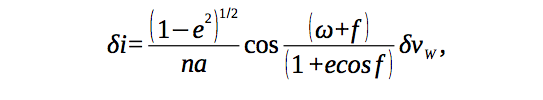
Where the changes in proper δi are computed with respect to the family center of mass, and f and ω are the (generally unknown) true anomaly and perihelion argument of the disrupted body at the time of impact.

If a family interacts with a secular resonance of node with a massive body, its inclination distribution will become more peaked and with larger tails when compared with a Gaussian one. As a consequence, the value of the Pearson kurtosis of the v_W component of the ejection velocity field, γ₂(v_W), will also increase. The minimum time needed to attain the current value of γ₂(v_W) for the v_W leptokurtic families can be used to set constraints on their ages. Three of the most v_W leptokurtic families are found in the highly inclined region of the central main belt: the Hansa, the Gallia, and the Barcelona families. For the Gallia family, the current value of  γ₂(v_W) can only be reached over the estimated family age if Ceres is considered as a massive perturber.

Overall, secular dynamics can provide invaluable hints for our understanding of the dynamical evolution of asteroid families and can set constraints on the ages and initial ejection velocity field that are not available for families that do not interact with secular resonances.

These findings are described in the article entitled Asteroid families interacting with secular resonances, recently published in the journal Planetary and Space Science. This work was conducted by V. Carruba from São Paulo State University (UNESP), D. Vokrouhlický from Charles University, and B. Novaković from the University of Belgrade.