Discovery Of A New Eastward-Propagating Coherent Atmospheric Structure: Equatorial Modon

Recently steady, long-living, slowly eastward-moving large-scale coherent twin cyclones, so-called “equatorial modons,” have been reported by Rostami & Zeitlin [1] in a moist-convective rotating shallow water model [2, 3]. This improved model has already applied to a study of the stability of jets and vortices on Earth and other planets [4, 5]. Some planetary-scale systems that propagate eastward are the Kelvin waves and the Madden–Julian Oscillation (MJO) [6]. The former propagate too fast (about 50 m/s), while the latter has a very low phase speed (about 5 m/s).

It worth mentioning that one of the enigmas of the tropical atmosphere is the dynamical nature of MJO, which is a periodically arising, large-scale pattern of enhanced deep convection which slowly moves eastward from the Indian Ocean over the maritime continent and dies out in the Pacific. The MJO was discovered about half a century ago by Madden and Julian in 1972 [6], and much is known about its structure and properties, yet its dynamical nature is not clearly understood. In particular, the question of why MJO events are slowly moving eastward remains unanswered. The climate models have difficulties in reproducing it, e.g. Kim et al. (2011) [7]. Kelvin waves, the only species of the equatorial waves that can produce steady large-scale eastward-moving structures, have a much faster velocity than MJO. There exist simplified models of MJO, either quasi-linear, e.g. Majda and Stechman (2009) [8], or essentially nonlinear, e.g. Haertel et al. (2013) [9], all of them essentially relying on the dynamical role of moisture.

The ability of a bunch of previous theoretical studies which usually present the MJO as a linear wave interaction between large-scale atmospheric flow and moist convection, in explaining both the scale and slowly eastward phase speed of MJO, is questionable. So, one of the challenges in tropical meteorology is an explanation of the dynamical nature of the MJO. There is no consensus on the explanation of the dynamical origin, formation, or development of this phenomenon. It is too early to claim that the presented equatorial modon by Rostami and Zeitlin is able to explain all dynamical features of the MJO; nevertheless, it shows the crudest features of the MJO. Eastward propagation along the equator, slow phase speed, hydro-dynamical coherent structure, the convergent zone of moist-convection, and having an exact solution is guaranteed by Rostami and Zeitlin’s Modon.

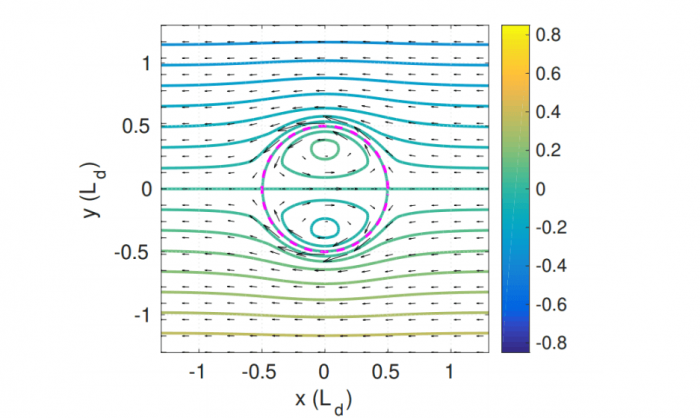
Fig. 1: Streamlines and velocity field of an asymptotic modon in co-moving frame. Dashed circle is separatrix with radius of modon. (Credit: M. Rostami)

The question, however, arises, whether there exist “dry” dynamical structures moving slowly eastwards along the equator, which could provide a “backbone” for the MJO events. The spectrum of linear equatorial waves being well established, such objects should be necessarily nonlinear. There do exist steady eastward-moving structures in a fluid layer on the mid-latitude f-plane, the so-called modons, exact dipolar solutions of the quasi-geostrophic (QG) equations discovered by Larichev and Reznik (1976) [10]. Although the classical modons were found analytically in the QG approximation, it was shown first by a computer-assisted analysis and then by direct numerical simulations that corresponding solutions exist also in the parent rotating shallow water (RSW) model on the f-plane.

In their pioneering paper, Yano and Tribbia [11] came up with an idea that the MJO could be related to such a modon in spherical geometry and showed that, like on the tangent plane, the equivalent barotropic modon persists in the RSW on the sphere. The archetype model for understanding the dynamics of the tropical atmosphere of RSW in the equatorial beta-plane. There is no consistent QG approximation at the equator, so the known modon solutions cannot be borrowed.

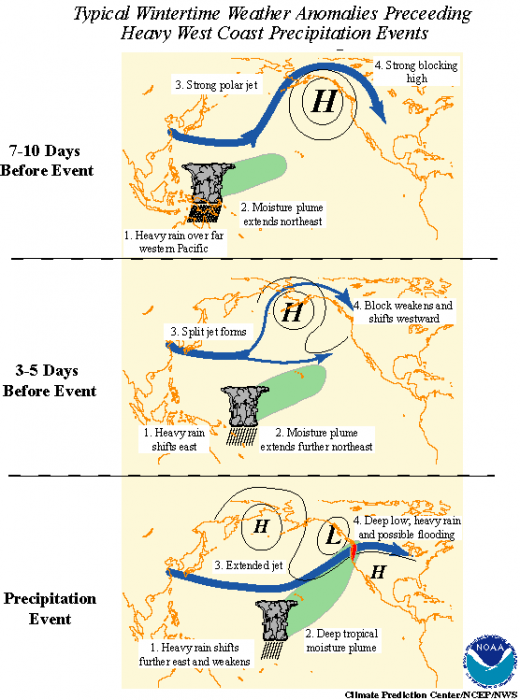
Fig. 2: Madden-Julian oscillation effects upon North American weather patterns. Eastward-moving tropical rainfall circulation drives north Pacific Ocean atmospheric circulation changes. “MJO North America rain” by the National Oceanic and Atmospheric Administration is licensed under CC0

The intuitive approach applied by Rostami & Zeitlin in their recent paper is a dynamical regime in RSW, called long-wave approximation in oceanography (Gill 1982) [12], which corresponds to small pressure variations and gives, to the leading order, equations which do allow for modon solutions. This quasi-barotropic regime is the RSW analog of Charney (1963) [13], a non-divergent balance model for equatorial atmosphere. The relevance of this model to large-scale tropical motions is supported by scale and data analyses. Rostami and Zeitlin constructed the modon solutions in this regime and used these asymptotic solutions to initialize high-resolution numerical simulations with the full RSW model, showing that coherent dipolar steady eastward-moving structures do arise and persist. They then showed that inclusion of moisture, with condensation and evaporation, enhances the modons without disrupting long-time coherence and produces some specific convective patterns.

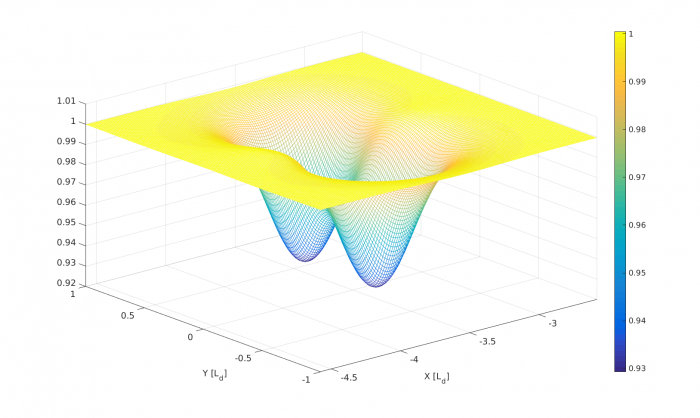
Fig. 3: Typical pressure configuration of the eastward-moving equatorial modon after adjustment. X and Y axes represent corresponding longitude and latitude with non-dimensional scale of Ld, that is Equatorial Rossby deformation radius. (Credit: M. Rostami)

References:

1. M. Rostami and V. Zeitlin, “Eastward-moving convection-enhanced modons in shallow water in the equatorial tangent plane.” J. Phys. of Fluids. 31, 021701 (2019). https://aip.scitation.org/action/cookieAbsent
2. M. Rostami and V. Zeitlin, “Improved moist-convective rotating shallow water model and its application to instabilities of hurricane-like vortices,” Q. J. R. Meteorol. Soc. 144, 1450 (2018).
   https://onlinelibrary.wiley.com/action/cookieAbsent
3. M. Rostami and V. Zeitlin, “ Influence of condensation and latent heat release upon barotropic and baroclinic instabilities of vortices in rotating shallow water f-plane model.” J. Geophysical & Astrophysical Fluid Dynamics, 111 (1), 1–31 (2016). https://www.tandfonline.com/action/cookieAbsent
4. M. Rostami, V. Zeitlin, A. Spiga, “On the dynamical nature of Saturn’s North Polar hexagon.” J. Icarus, 297, 59-70 (2017). https://linkinghub.elsevier.com/retrieve/pii/S0019103516305978
5. M. Rostami, V. Zeitlin, L. Montabone, “On the role of spatially inhomogeneous diabatic effects upon the evolution of Mars’ annular polar vortex.” J. Icarus, 314, 376-388 (2018).
   https://linkinghub.elsevier.com/retrieve/pii/S0019103517306073
6. R. Madden, P. Julian, “Description of global-scale circulation cells in the tropics with a 40-50 day period.” J. Atmos. Sci. 29, 1109–1123 (1972).
7. D. Kim, A. Sobel, E. Maloney, D. Frierson, I. Kang, “A systematic relationship between intraseasonal variability and mean state bias in AGCM 266 simulations.” J. Climate 24, 5506–5520 (2011).
8. A. J. Majda, S.N. Stechman, “The skeleton of tropical intraseasonal oscillations.” PNAS, 106, 8417–8422 (2009).
9. P. Haertel, K. Straub, A. Fedorov, “Lagrangian overturning and the Madden – Julian Oscillation.” Q. J. Roy. Met. Soc. 140, 1344–1361 (2013).
10. V. D. Larichev and G. M. Reznik, “Two-dimensional solitary Rossby waves,” Dokl. USSR Acad. Sci. 231, 1077 (1976).
11. J.-I. Yano and J. Tribbia, “Tropical atmospheric Madden-Julian oscillation: A strongly nonlinear free solitary Rossby wave?,” J. Atmos. Sci. 74, 3473 (2017).
12. A. Gill, “Atmosphere-Ocean Dynamics.” (Academic Press, 1982).
13. J. Charney, “A note on large-scale motions in the tropics,” J. Atmos. Sci. 20, 607 (1963).