Building Performance Assessment For Earthquakes Breaks New Ground With Study On Critical Orientation Using Lateral Force Analysis

One of the main purposes of the earthquake-related standards (e.g. EAK 2003; CEN 2004; Regulatory Guide 1.92 2006; NTC 2008; ASCE 2014) is to provide guidelines for the safe design and construction of structures against seismic loads. Modern standard provisions, however, are restricted by the current level of knowledge.

One aspect in which our knowledge is still limited is the ability to predict the exact location of the next earthquake. Taking this into account, in order to reassure that our structure will be able to resist a future earthquake generated at any location, the worst possible direction of attack should be studied. In the worst direction, we refer to the direction that will cause the most unfavorable effect on the structure.

The term angle of seismic incidence is used to refer to the orientation of a seismic action with respect to the building as represented in Figure 1 and denoted as θ. The angle θ that results in the most unfavorable effect is termed critical angle of incidence.

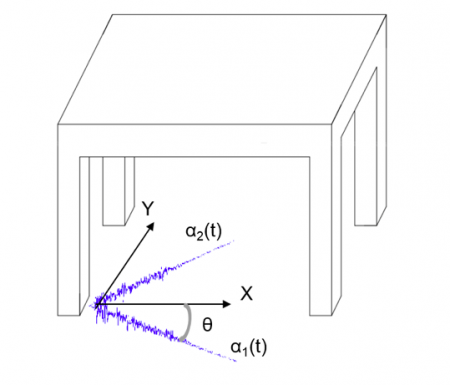Figure 1. The angle of seismic incidence (θ) is the angle between the building’s structural axes, X and Y, and the input seismic action. Credit: Despoina Skoulidou

Most of the existing seismic provisions recognize the importance of the critical angle of incidence and require from the practitioners to account for it. However, the critical angle of incidence is not easy to define. Several studies performed during the past years have proven that each building has different critical angles of incidence that also vary for the different parameters (e.g. column force, story displacement etc).

Additionally, each seismic action has been found to cause the most unfavorable demand under a different angle of incidence. Moreover, several structural characteristics affect the critical angle, such as the simulation of the materials when the building is analyzed with nonlinear material properties. Thus, it results that is it not possible to know the critical angle a priori.

Since straightforward solutions to derive the critical angle of incidence are practically inexistent for most of the analysis procedures allowed by the standards, the practitioners are required to perform parametric analysis by considering multiple angles of incidence in order to derive the critical one. Such an approach, however, appears to be impractical and sometimes impossible for regular use.

Continuous studies with respect to the definition of the critical angle have resulted in the derivation of useful solutions to the problem (Menun and Der Kiureghian (1998), Athanatopoulou (2005)). Such a solution was also derived for the simplest and most frequently used method of analysis, the Lateral Force Analysis, and will be presented herein base on the original paper by Skoulidou and Romao (2017). The procedure will be presented for the case of a single story structure, while its extension for multi-story buildings accompanied by examples of the application can be found in the original document.

In LFA the seismic action corresponds to an acceleration response spectrum, which is a normalized average spectrum. The acceleration response spectrum consists of a four-branched equation, which is a function of the fundamental structural period along a given direction. An example of an acceleration response spectrum is presented in Figure 2.

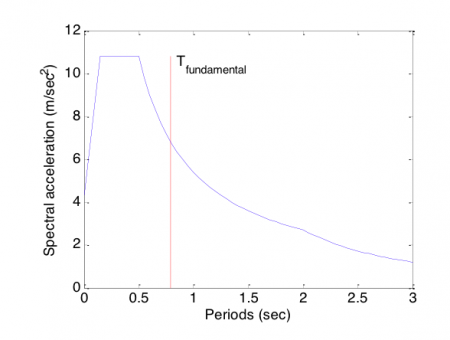Figure 2. Acceleration response spectrum. Credit: Despoina Skoulidou

The spectral acceleration, Sa, that corresponds to the fundamental period is then multiplied by the mass in order to calculate the input seismic force, F, along the respective direction.

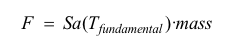                    (1)

Moreover, in LFA the building is modeled using the finite element method and considering linear elastic material properties. This modeling technique allows for the full description of the static behavior of the building based on its principal reference system. In the principal reference system, the uncoupled fundamental structural period, T_unc, of the building along any direction has been proven to fall on an ellipse, and thus it can be described by well-known mathematical expressions, as a function of the respective direction (or the angle of incidence, θ):

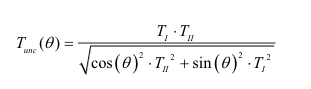(2)

where T_I and T_II, correspond to the fundamental periods of the building along the two principal directions.

By substituting the expression of the uncoupled fundamental period, defined in Equation 2, in the expression of the spectrum and multiply it by the mass, as shown in Equation 1, the input seismic force is obtained only as a function of the angle of seismic incidence:
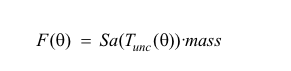      (3)

Hence, the maximization of the input force can be deduced by maximizing Equation 3. Such a maximization can be achieved by equalizing the derivative of Equation 3 to zero and solving with respect to the angle. The obtained angle is the critical angle of incidence.

These findings are described in the article entitled Critical orientation of earthquake loading for building performance assessment using lateral force analysis, published in the journal Bulletin of Earthquake Engineering. This work was led by Despoina Skoulidou from the University of Porto.

References:

• ASCE (2014) Seismic evaluation and retrofit of existing buildings (ASCE/SEI 41-13). American Society of Civil Engineers, Reston, Virginia, USA
• Athanatopoulou AM (2005) Critical orientation of three correlated seismic components. Engineering Structures 27(2): 301–312
• EAK (2003) Greek code for earthquake resistant design of structures. Ministry of Environment, Planning and Public Works. Athens, Greece
• CEN (2004) EN1998-1 Eurocode 8: Design of structures for earthquake resistance, part 1: general rules, seismic actions and rules for buildings. European Committee for Standardization
• Federal Emergency Management Agency (2012) Seismic performance assessment of buildings. FEMA P58 report, Washington, DC
• Menun C, Der Kiureghian A (1998) A Replacement for the 30%, 40%, and SRSS rules for multicomponent seismic analysis. Earthquake Spectra. 14(1): 153-163
• NTC (2008) Norme tecniche per le costruzioni. Decreto del Ministero delle Infrastrutture. Supplemento ordinario n.30 alla Gazzetta Ufficiale della Repubblica Italiana n.29 del 4/02/2008, Italy (in Italian)
• Regulatory Guide 1.92 (2006) U.S. Nuclear Regulatory Commission, Office of Nuclear Regulatory Research. Washington, DC
• Skoulidou, D., & Romão, X. (2017). Critical orientation of earthquake loading for building performance assessment using lateral force analysis. Bulletin of Earthquake Engineering, 15(12), 5217-5246.