Bending (But Not Breaking) The Second Law Of Thermodynamics Using A “Thermal Inductor”

The fundamental laws of thermodynamics

The first law of thermodynamics is widely known, even outside scientific classrooms, because it introduces “heat” into the balance of energy conservation. In a simplified version, we can say that the sum of the heat and of the work done on a body corresponds to the change in the total energy of the body.

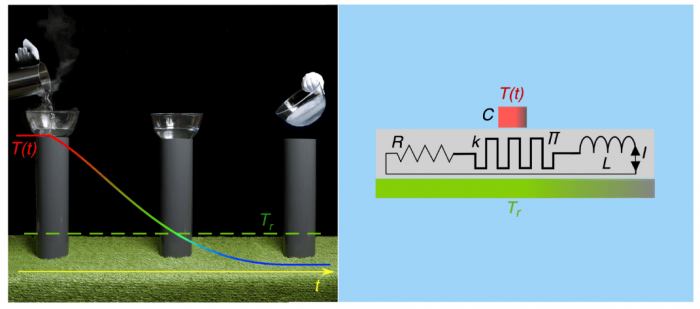
Fig. 1: The “magic” cooling effect (left symbolic picture) is produced by a combination of a Peltier element (Π) and an inductor (L) (right). The quantities k and R are parasitic contributions, which are detrimental to the cooling performance. Figure courtesy A. Schilling and A. M. Mangham

The second law of thermodynamics, on the other hand, sometimes causes confusion because several different versions of this law can be found in textbooks. One of these versions is quantitative and stringently formulated but also quite abstract, saying that the entropy in an isolated system is constant or increases over time, but never decreases.

Other formulations of this law may leave some room for interpretations, such as the saying, “Heat can flow only from hot to cold.” The fact that this statement is entirely wrong is obvious: in an ordinary kitchen refrigerator, heat is flowing from cold to hot all the time because a compressor connected to an electrical outlet does work on the fridge. Therefore, one could re-formulate the above statement as, “Heat can flow only from hot to cold unless there is some kind of external intervention.” Such an intervention would do the work to force heat to flow from cold to hot and, ultimately, always requires an external energy source.

Analogy between thermal and electric circuits

Those students who had classes in thermodynamics and electricity may know another interesting fact, which may appear at first glance unrelated to the second law. Heat currents that occur as soon as two connected bodies equalize their temperatures and electrical currents in an electric circuit can be described with the same mathematical formalism. The electric analog to a heat current is the electric current, heat corresponds to electric charge, and temperature to an electric voltage. Even certain simple electric components have a thermal counterpart. An electric capacitor is equivalent to heat capacity, and the electric conductivity (or electric resistance) corresponds to  thermal conductivity (or thermal resistance), respectively. From this point of view, the equilibration of temperatures between two bodies is similar to the discharge of an electric capacitor.

Another widely-used component in electric circuits is the electric inductor. It usually consists of a wire wound to a coil and is sometimes filled with a magnetizable material (such as iron) to enhance the value of its inductivity. Connecting it to an electric capacitor results in a closed circuit that allows for oscillations of charge, current, and voltage with time, where the corresponding quantities periodically change their sign. The frequency of this oscillation is essentially determined by the value of the capacitance and the inductance.

Does a “thermal inductor” exist?

However, no thermal analog to an electric inductor has been reported up to date that would deserve the name. All suggestions to construct such a “thermal inductor” that have been made in the literature were based on non-equilibrium processes involving the flow of matter or time-dependent transient processes, so that the bodies under consideration never had well defined thermodynamic variables. It has often been argued that the existence of a “thermal inductor” would violate the second law of thermodynamics. Indeed, a thermal oscillating circuit, consisting of such a “thermal inductor” and a heat capacity, would make it possible to create an oscillating heat current where the temperature difference between two bodies perpetually changes its sign. As a consequence, heat would temporarily flow from the colder to the warmer object so that the colder body is further chilled down.

Oscillating thermal currents using a “thermal inductor”

One might expect that the invention of a device behaving like a “thermal inductor” would involve the highest technology and advanced, state-of-the-art materials. Already back in 2011, we had performed experiments with thermal oscillators, with the aim to measure heat capacities with the highest precision. To do this, we simply switched a commercially available Peltier element with an electric inductor (i.e., a coil) in series and connected them thermally with the heat capacity to be measured. Peltier elements are widely used in present cooling technology. They can transform electric currents into heat currents, and conversely temperature differences to electric voltages. The resulting device behaved exactly like a thermal oscillating circuit with heat capacity and a “thermal inductor.” This experiment was operated as an “active” circuit with an external energy source and electronics connected to compensate for electric losses and to maintain a steady resonant oscillation for a long time. This made it possible to accurately measure the resonant frequency and to finally calculate the value of the heat capacity.

At that time and with the electrical components used, disconnecting the externally-powered driving circuit only allowed for an over-damped behavior once the system was allowed to relax by itself. By re-considering the corresponding thermal and electrical equations (ironically, this is a task that could be easily reproduced by a student in engineering in the first semesters) we realized that also oscillatory solutions for the variation of temperature and heat are possible, even in the absence of an external driving source. In other words, once you create an initial temperature difference between two bodies, disconnect them from external energy sources and allow them to subsequently exchange heat through the thermal inductor, you should be able to see extended periods of time where heat is flowing from cold to hot each time when the temperature difference changes sign, notably without any external intervention from outside.

The experiment

Fig. 2: The 9 g copper cube on top of a Peltier element thermally connected with a large copper block as the thermal bath. Figure courtesy A. Schilling

As simple as it sounds, we still had to make some effort to find a decently efficient commercial Peltier element (which was fairly easy), but also to find electric inductors with no electrical losses, i.e., superconducting coils, with the desired specifications. We then heated an object (9 grams of copper) to 104 degrees Celsius and connected it with one side of the Peltier element. A heat bath held at ambient temperature (≈ 22 degrees Celsius) was placed to the other side of that element. After a while, the temperature of the copper dropped significantly below that of the thermal bath. In the language of mathematics, the oscillating temperature difference changed sign after it passed zero for the first time.

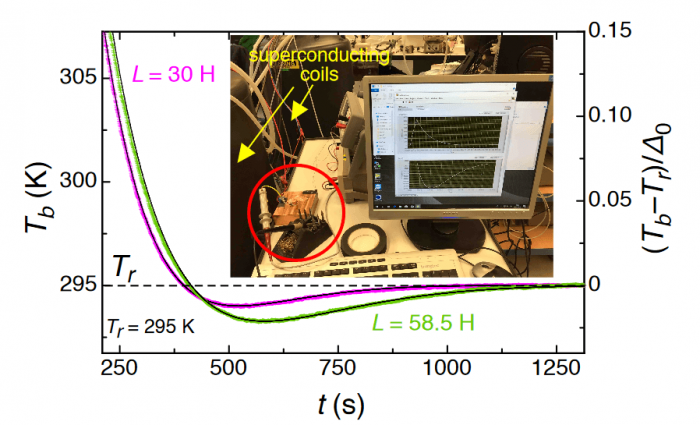
Fig. 3: Cooling effect below ambient temperature for two values of inductance L of the superconducting coils. Figure courtesy A. Schilling.

A subtle but important point to mention here is the fact the heat was directly flowing from cold to hot in these processes, without ever being converted into any other form of energy. It turned out that the magnetic energy stored in the coil is negligible, and therefore the heat must have flown directly from cold to hot. The maximum temperature difference to ambient temperature reached only a disappointingly small value of ≈ 2 degrees, however, which was mainly due to the limited performance of the used commercial Peltier element, as we shall see below.

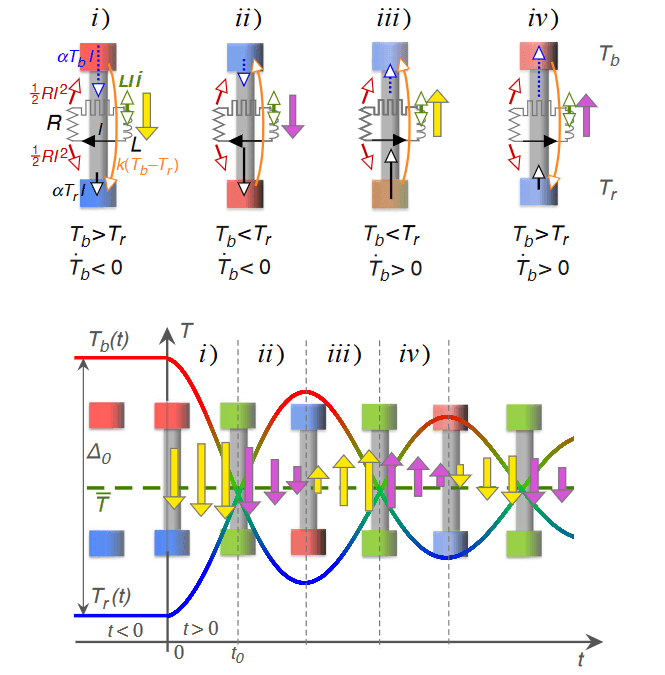
Fig. 4: Sketch of the individual contributions to the flow of heat during an experiment when heat is flowing from (filled yellow arrows) or to (filled purple arrows) the warmer end of the Peltier element. Figure courtesy A. Schilling.

Significance and relation to the second law of thermodynamics

Admittedly, our work primarily represents at this stage a proof-of-principle study. Nonetheless, the experiments challenge to some extent our ordinary perception of the flow of heat, which may have been misguided by certain shortened versions of the second law of thermodynamics in some textbooks. The original version by Clausius states that the flow of heat from cold to hot must be associated with, “some other change, connected therewith, occurring at the same time.” This “other change” may mean either an external intervention or, as in our case, the fact the used electric inductor, an integral part of the thermal connection, is perpetually changing its state due to the oscillating electric current flowing within the “thermal inductor” circuit.

Even before we performed these experiments, we knew, of course, that the second law of thermodynamics would not be violated. To prove this in a stringent way, we considered the change in entropy of the whole system and showed that it is really strictly monotonically increasing with time. Some deeper consideration even allowed us to predict how far such a cooling process below ambient temperature might reach in principle. Assuming a maximal thermodynamic efficiency of the Peltier element (a criterion which is notably taken from another version of the second law) we concluded that one might reach – 47 degrees Celsius under the same experimental conditions.

With future technological progress in thermoelectric devices and superconductors, large amounts of hot solid, liquid, or gaseous materials could, in principle, be cooled down far below room temperature without any external energy source or moving parts, and the passive thermal circuit could be used as often as desired.